Module 1: Time vs Frequency Domains

Summary

This script explains the difference between the time and frequency domains in signal analysis. It describes how the time domain reflects real-world experiences and is represented by plots over time, while the frequency domain is more abstract, focusing on a signal's frequency components. The Fourier transform is used to convert between the two. Practical tools such as oscilloscopes and spectrum analyzers are discussed, along with the importance of understanding low-power signals and how filters affect signals in both domains. Concepts like negative frequencies and real vs. imaginary components are also explored.

Takeaways

• 🕰️ Time domain represents the familiar way we perceive the world, where events occur sequentially over time.
• 📊 The time domain is typically represented by a plot with time on the x-axis.
• 🔄 The frequency domain is an abstract concept that represents signals as a sum of frequency components.
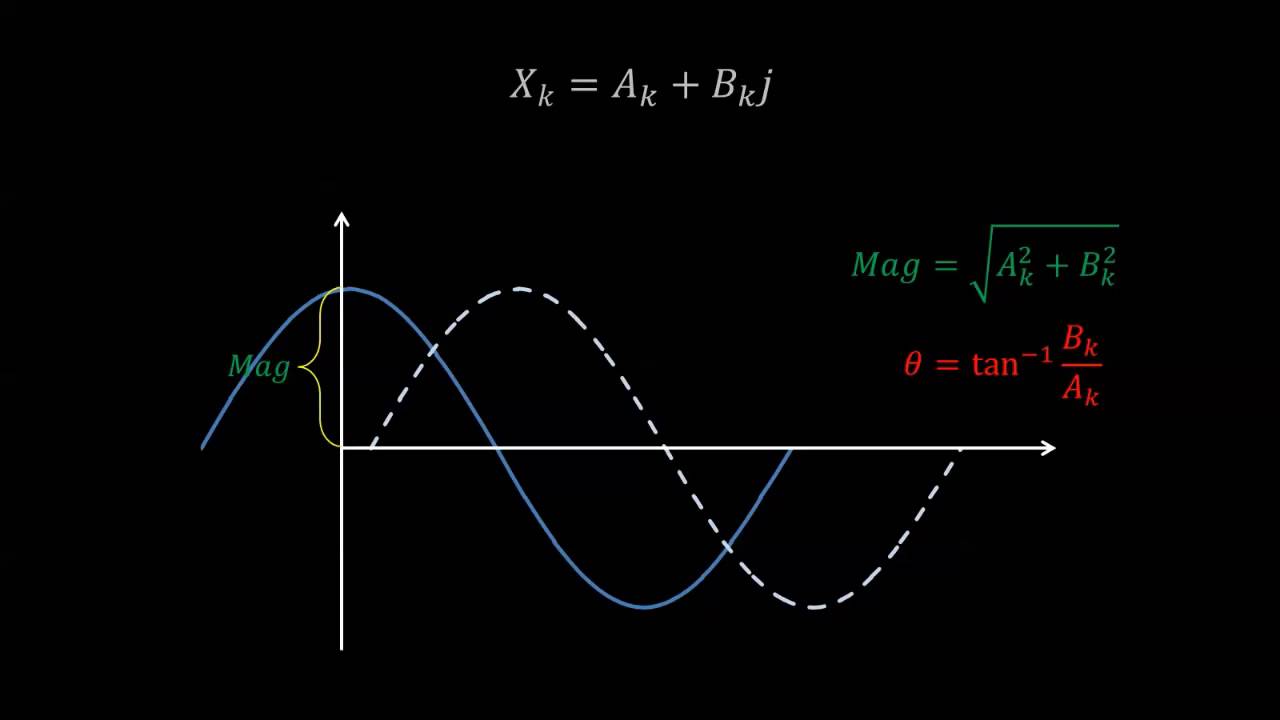
• 🎶 Using Fourier series, any time-domain signal can be broken into cosines and sines in the frequency domain.
• 🔢 Engineers often use frequency (F) in analysis, but sometimes work with Omega (ω) in analytical calculations.
• 📡 Time-domain signals are measured using an oscilloscope, while frequency-domain signals are measured using a spectrum analyzer.
• 📉 Advanced features of spectrum analyzers are necessary to detect very low-power signals like microwatts or picowatts.
• 🔄 The Fourier transform allows conversion between time and frequency domains, but changes in one domain affect the other differently.
• 📏 Filters in the frequency domain can simplify signal processing, smoothing signals in the time domain.
• 🌀 Real signals contain both positive and negative frequency components, which are necessary to represent fully measurable real-world signals.

Q & A

What is the time domain, and why is it familiar to us?

The time domain is the way we perceive events as they occur in real life, where time moves forward, and events happen over time. It's familiar because it reflects our everyday experiences and is typically represented by a plot versus time.

How does the frequency domain differ from the time domain?

The frequency domain is an abstract concept that helps us analyze signals by breaking them down into frequency components, such as cosines and sines. Unlike the time domain, which deals with signals over time, the frequency domain focuses on the magnitude and phase of these frequency components.

What is the role of the Fourier series in signal processing?

The Fourier series allows us to break any time-domain signal into a series of cosines and sines. This decomposition makes it easier to work with signals by analyzing their frequency components, particularly in the frequency domain.

Why do engineers often use frequency (F) instead of angular frequency (Omega)?

Engineers commonly use frequency (F) because most instrumentation measures in terms of frequency. However, angular frequency (Omega) is used in analytical calculations, often when results are expressed in radians. Engineers can switch between the two using a conversion formula.

What instruments are used to measure time and frequency domain signals?

To measure time-domain signals, an oscilloscope is used. For frequency-domain signals, a spectrum analyzer is employed. Both instruments provide valuable insights into the respective domains of the signals.

How can you move between the time and frequency domains?

The Fourier transform allows for the conversion of signals from the time domain to the frequency domain and vice versa. Changes in one domain affect the other, although the changes are not identical.

What happens to a signal when it passes through a low-pass filter?

In the frequency domain, a low-pass filter removes high-frequency components, which correspond to sharp edges in the time domain. As a result, the signal becomes smoother in the time domain.

What does the Fourier transform of a square wave look like?

The Fourier transform of a square wave produces a sinc function in the frequency domain. This transform illustrates how a square wave, with sharp edges in the time domain, contains a wide range of frequency components.

What are real and negative frequencies, and how are they related?

In the frequency domain, real signals have both positive and negative frequency components. Negative frequencies appear due to the complex nature of signals, which can be expressed as a combination of e^(jωt) and e^(-jωt). These components help create a real signal by canceling out the imaginary parts.

Why do we need both positive and negative frequency components to form a real signal?

To form a real signal, we combine both positive and negative frequency components because a single component would result in a complex (imaginary) signal. Combining them cancels the imaginary parts and ensures the signal is entirely real and measurable.