Bonds as springs | Spectroscopy | Organic chemistry | Khan Academy
Summary
TLDRThis educational video script explores the concept of molecular vibrations through the analogy of a spring-mass system, illustrating how the frequency of oscillation is influenced by the spring constant (k) and the reduced mass (μ). The script explains that stronger bonds, represented by a higher k value, lead to faster vibrations, while lighter atoms with smaller reduced mass also result in higher frequencies. The discussion includes the calculation of the reduced mass for different types of bonds and how it affects the vibrational frequency, providing a clear understanding of the principles behind infrared spectroscopy.
Takeaways
- 🔍 Infrared (IR) radiation of certain frequencies can cause molecular bonds to stretch, similar to a spring.
- 📚 Hooke's law is applied to model the stretching vibration of a bond, where the force exerted by the spring is proportional to the displacement and in the opposite direction.
- 🎚 The spring constant (k) is a measure of the stiffness of the spring, with a higher k indicating a stiffer spring and a stronger bond.
- 📉 The displacement (delta x) from the original position is directly proportional to the force exerted by the spring, as per Hooke's law.
- 🔄 The frequency of oscillation for a spring-mass system is given by the formula \( \frac{1}{2\pi} \sqrt{\frac{k}{m}} \), where m is the mass of the object attached to the spring.
- ⏱ The period of oscillation is the time it takes for one complete oscillation, and it is inversely related to the frequency.
- 🔝 An increase in the spring constant (k) results in a higher frequency of oscillation, indicating faster vibrations.
- 🔽 An increase in the mass (m) of the object attached to the spring results in a lower frequency of oscillation, indicating slower vibrations.
- 🤔 The concept of reduced mass is introduced for systems where both ends of the spring (bond) have moving masses, calculated as \( \frac{m_1 \times m_2}{m_1 + m_2} \).
- 🔗 The frequency of vibration is influenced by both the strength of the bond (spring constant) and the reduced mass of the system, with stronger bonds and lighter atoms leading to higher frequencies.
Q & A
What is the analogy used in the script to explain the stretching vibration of a chemical bond?
-The script uses the analogy of a spring to explain the stretching vibration of a chemical bond. The bond is modeled as a spring that obeys Hooke's law, where the stretching vibration is likened to a spring-mass oscillation.
According to Hooke's law, how is the force of a spring related to its displacement?
-Hooke's law states that the force of a spring (F) is equal to the negative product of the spring constant (k) and the displacement (x) from its equilibrium position, represented as F = -kx. The negative sign indicates that the force is a restoring force, acting to return the spring to its original position.
What is the significance of the spring constant (k) in the context of the script?
-The spring constant (k) is significant because it represents the stiffness of the spring. A higher value of k indicates a stiffer or stronger spring, which results in a greater force being exerted for a given displacement, and consequently, a higher frequency of oscillation.
How does the mass of the object attached to the spring affect the frequency of oscillation?
-The frequency of oscillation is inversely related to the mass (m) of the object attached to the spring. As the mass increases, the frequency of oscillation decreases, leading to slower oscillations. This is derived from the formula for the frequency of oscillation: f = 1/(2π√(k/m)), where f is the frequency, k is the spring constant, and m is the mass.
What is the term for the distance a box is moved from its original position in the script's example?
-In the script's example, the term for the distance a box is moved from its original position is 'displacement,' represented by the symbol 'delta x' (Δx).
How is the frequency of oscillation calculated for a spring-mass system?
-The frequency of oscillation for a spring-mass system is calculated using the formula f = 1/(2π√(k/m)), where f is the frequency, k is the spring constant, and m is the mass of the object. This formula is derived from setting the force equation equal to mass times acceleration and solving for frequency.
What is the concept of reduced mass, and how is it used in the context of the script?
-The concept of reduced mass is used when considering a system with two masses oscillating together, such as in a chemical bond. It is calculated as μ = (m1*m2) / (m1 + m2), where m1 and m2 are the masses of the two objects. The reduced mass allows for the calculation of the frequency of oscillation when both masses are moving, as opposed to just one.
How does the script demonstrate the calculation of reduced mass for a carbon-hydrogen bond?
-The script demonstrates the calculation of reduced mass for a carbon-hydrogen bond by using the atomic masses of carbon (12 AMUs) and hydrogen (1 AMU). The reduced mass (μ) is calculated as μ = (12*1) / (12 + 1) = 12/13 ≈ 0.923 AMUs.
What is the effect of increasing the reduced mass on the frequency of vibration, as explained in the script?
-According to the script, increasing the reduced mass results in a decrease in the frequency of vibration. This is because the frequency of oscillation is inversely related to the reduced mass, as shown in the formula f = 1/(2π√(k/μ)), where μ is the reduced mass.
How does the script explain the difference in frequency of vibration between a carbon-carbon single bond and a carbon-carbon double bond?
-The script explains that while the reduced mass remains the same for both a carbon-carbon single bond and a double bond, the spring constant (k) is effectively doubled for the double bond, assuming it is twice as strong as the single bond. This increase in k leads to an increase in the frequency of vibration for the double bond.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

De qué depende el periodo para una masa en un resorte | Física | Khan Academy en Español

Kimia Kuantum - 04A Osilator Harmonik #1 - Klasik

Oscillations Demo: Mass Spring System

Contoh Soal Undamped Free Vibration (Seri Getaran Mekanis part2)

Aula 1 – Movimentos Periódicos e Introdução ao MHS
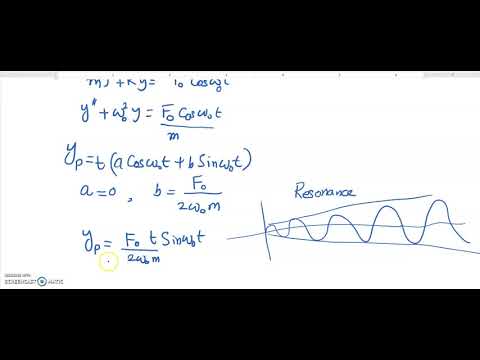
Modeling Forced Oscillations of Mass Spring System clip 3
5.0 / 5 (0 votes)
