AA-U1-W3-ML1 Physics of Orbits 1 - Energy
Summary
TLDRThis educational script delves into the physics of orbital motion, contrasting the 'forces approach' using Newton's laws with the 'energy approach' focusing on conservation of energy. It explains how the total energy of a system, combining kinetic and potential energies, can predict the behavior of astronomical objects in orbit. The script introduces concepts like angular momentum and effective potential energy, illustrating how they dictate the shape of orbits and the stability of circular paths. It also touches on the challenges of sending probes close to massive objects due to energy barriers and the importance of angular momentum in preventing objects from spiraling into the central mass.
Takeaways
- 🔍 There are two primary approaches to solving physics problems: the forces approach, which uses Newton's laws, and the energy approach, which applies the conservation of energy.
- 📚 The forces approach involves solving differential equations derived from Newton's second law, often starting with simple scenarios like constant velocity or acceleration.
- 🔄 The energy approach sums the kinetic and potential energies of a system and uses the conservation of energy to solve for system states, often involving integral equations.
- 🌌 In orbital mechanics, the energy method helps analyze the motion of astronomical objects by considering their kinetic and potential energies.
- 📉 The effective potential energy, which includes both potential and a component of kinetic energy, is crucial for understanding orbits and is plotted against radius to visualize orbital behavior.
- ⚫ The effective potential energy curve shows an infinite barrier at the center, preventing objects from spiraling into the central mass, illustrating the conservation of angular momentum.
- 🔵 At the minimum of the effective potential energy curve, an object will maintain a constant radius (Rc), indicative of a stable circular orbit.
- 🔴 The location of the minimum (Rc) in the effective potential energy curve depends on the angular momentum of the orbiting object and the mass of the central body.
- 🔄 Perturbations from the minimum radius result in elliptical orbits, where the radial coordinate executes simple harmonic motion, approximating an elliptical path.
- 📈 The energy method provides a clear picture of how objects in orbit respond to changes in energy and angular momentum, predicting stable orbits and the effects of perturbations.
Q & A
What are the two general approaches to solving problems in physics?
-The two general approaches to solving problems in physics are the forces approach and the energy approach. The forces approach involves determining all the forces acting on a system and applying the equations of motion, typically Newton's laws. The energy approach involves writing down the total energy of the system as a sum of kinetic and potential energy and applying the law of conservation of energy.
How does the forces approach typically use Newton's second law of motion?
-The forces approach uses Newton's second law of motion, which states that the force acting on an object is equal to the mass of the object times its acceleration. This approach often results in differential equations that need to be solved to find the position, velocity, and acceleration of an object over time.
What is the significance of angular momentum in orbital motion?
-Angular momentum is a key characteristic of an orbit and plays a crucial role in determining the shape and stability of an orbit. It prevents an object from spiraling into the central body and acts as an energy barrier. The conservation of angular momentum dictates that an object with any tangential velocity component cannot fall into the central object.
How is the energy per unit mass of a test particle orbiting a central mass derived?
-The energy per unit mass (epsilon) of a test particle orbiting a central mass is derived by considering the kinetic energy of the particle and the gravitational potential energy. It is expressed as epsilon = 1/2 * V_R^2 + L^2 / (2 * m * R^2) - G * M / R, where V_R is the radial velocity, L is the angular momentum, m is the mass of the test particle, R is the radial distance, and G * M is the gravitational potential energy.
What does the effective potential energy represent in the context of orbital motion?
-The effective potential energy in the context of orbital motion represents a combination of the actual potential energy due to gravity and the potential energy associated with the angular momentum of the orbiting object. It is useful for visualizing and understanding the behavior of orbits, especially in terms of stability and the tendency of objects to move towards energy minima.
Why is it difficult for a probe to get close to the Sun?
-It is difficult for a probe to get close to the Sun because it must overcome the energy barrier created by the conservation of angular momentum. The probe needs to have sufficient energy to either climb up the centrifugal energy barrier or burn away its angular momentum to spiral in towards the Sun, which requires a colossal amount of fuel.
What is the significance of the minimum in the effective potential energy curve?
-The minimum in the effective potential energy curve corresponds to the most stable orbit, where the total energy of the system is minimized. This minimum represents the radius at which an object will naturally tend to stay if placed there, and it is the radius of a circular orbit for a given amount of angular momentum.
How does the concept of simple harmonic motion relate to orbital motion?
-In orbital motion, if an object is placed close to the minimum of the effective potential energy curve, it will execute simple harmonic motion in the radial direction. This means that the radial distance from the central object will oscillate back and forth in a sinusoidal pattern, resulting in an elliptical orbit.
What is perturbation theory and how does it relate to solving differential equations in orbital motion?
-Perturbation theory is a mathematical method used to approximate the solution to a problem by starting with a known solution to a simpler problem and then making small adjustments or 'perturbations' to account for the complexities of the actual problem. In the context of orbital motion, it can be used to solve differential equations by considering small deviations from a known, simpler orbit, such as a circular orbit.
What is the relationship between the conservation of energy and Newton's second law in the context of orbital motion?
-In the context of orbital motion, the conservation of energy and Newton's second law are closely related. The conservation of energy principle states that the total energy of a system remains constant, which can be expressed in terms of the effective potential and kinetic energy. Differentiating the total energy with respect to a variable (like radius) and setting it to zero, as required by the conservation of energy, leads to an equation that is essentially Newton's second law, showing the force acting on the object.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
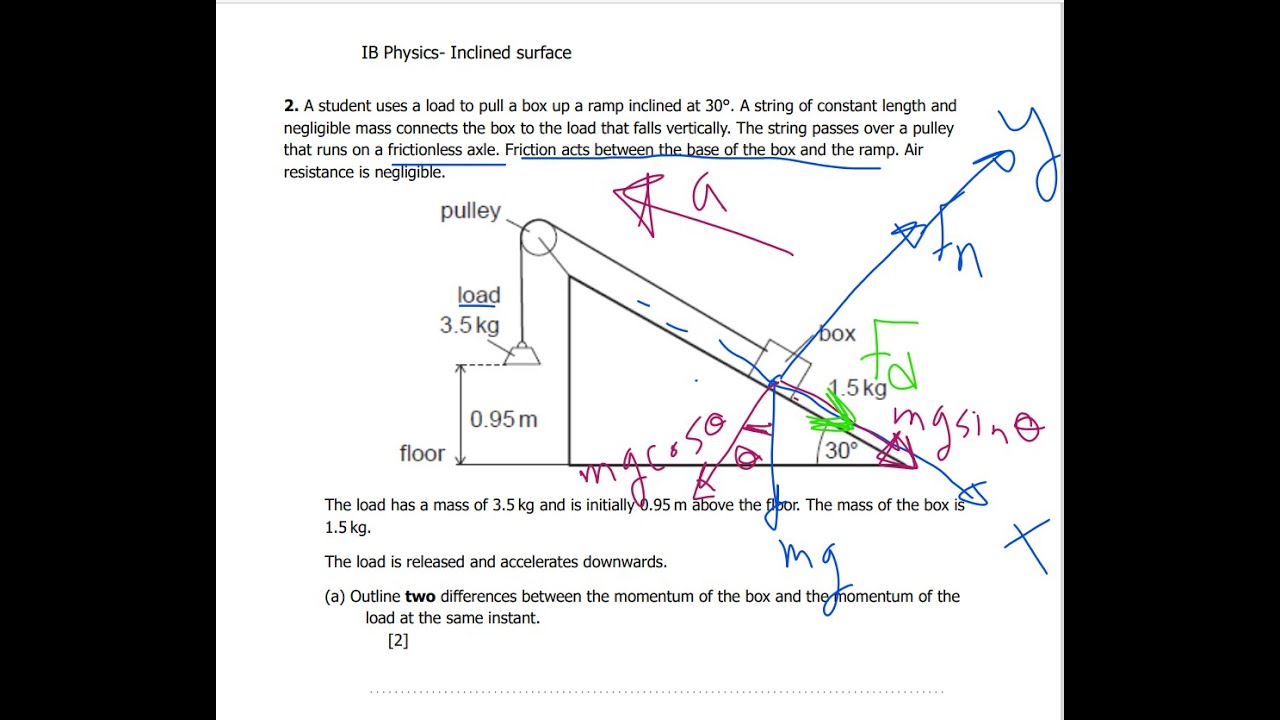
IB Physics-Theme-A2- A student uses a load to pull a box up a ramp inclined

Usaha dan Energi • Part 6: Contoh Soal Hubungan Usaha, Energi, dan Daya (1)

Edexcel IAL Mechanics - A Level Physics Revision

Graphing Energy (VPython for Physics 1)

Quantidade de Movimento Explicada (Momento) | Episódio 3

Gaya dan Hukum hukum Newton
5.0 / 5 (0 votes)
