The Distributive Property (M2 2.1 Notes)
Summary
TLDRThis educational video script focuses on polynomials, emphasizing the distributive property for multiplying and factoring. It covers combining like terms, expanding on the distributive property, and applying it to binomials. The script also introduces the zero product property for solving equations. Each concept is explained with examples to ensure a thorough understanding before moving on to the next topic.
Takeaways
- 📚 The lesson focuses on polynomials, specifically on multiplying and factoring them, with an emphasis on the distributive property.
- 🔢 Adding and subtracting like terms is covered, where coefficients are combined without changing exponents.
- 🧩 Parentheses are discussed in the context of polynomials, highlighting that a plus sign before parentheses does not affect the terms inside, but a minus sign does.
- 🔄 The distributive property is explained as a method to interact between multiplication and addition, and it is also used in reverse for factoring.
- 🔢 When multiplying terms, exponents change, which is different from addition or subtraction where they remain the same.
- 🔍 Factoring is demonstrated by finding the greatest common factor and dividing each term by it, which can be checked by multiplying the factors.
- 📉 The zero product property is introduced as a tool for solving equations where a product of two factors equals zero, implying at least one factor must be zero.
- 🚫 The importance of understanding the underlying principles before using shortcuts is stressed to avoid common mistakes.
- 📘 The process of multiplying binomials is detailed, emphasizing the step-by-step application of the distributive property rather than relying on shortcuts.
- ✅ The lesson concludes with an example of using the zero product property to solve equations by factoring and setting each factor equal to zero.
Q & A
What is the main focus of Unit 2 in the transcript?
-Unit 2 primarily focuses on polynomials, specifically on multiplying and factoring polynomials, with an emphasis on the distributive property.
How does the distributive property apply to polynomials?
-The distributive property allows for the interaction between multiplication and addition in polynomials. It states that for any numbers a, b, and c, the expression a(b + c) is equivalent to ab + ac.
What is the rule for combining like terms in polynomials?
-When combining like terms in polynomials, you add or subtract the coefficients while keeping the variable part unchanged. For example, x^2 + x^2 results in 2x^2.
Why are parentheses important when there's a negative sign in front of them?
-Parentheses are important when there's a negative sign in front of them because the negative sign must be distributed to every term inside the parentheses, which affects the signs of the terms.
What is the difference between multiplying and adding or subtracting in terms of exponents?
-When adding or subtracting, the exponents of like terms are not changed; only the coefficients are combined. However, when multiplying, the exponents are added together, as seen in expressions like x^2 * x^2 = x^(2+2) = x^4.
How does the zero product property help in solving equations?
-The zero product property states that if the product of two factors equals zero, then at least one of the factors must be zero. This property is used to solve equations by factoring and setting each factor equal to zero.
What is a common mistake made when distributing a negative sign across terms in parentheses?
-A common mistake is to only distribute the negative sign to the first term inside the parentheses and not to all terms, which leads to an incorrect solution.
Why is it important to understand the distributive property before using shortcuts for multiplying binomials?
-Understanding the distributive property before using shortcuts for multiplying binomials is important because it provides a solid foundation for why the shortcuts work, ensuring that the process is correctly applied and understood.
How does the process of factoring relate to the distributive property?
-Factoring is essentially the reverse of using the distributive property. It involves finding the greatest common factor and expressing the polynomial as a product of its factors, which can then be expanded using the distributive property.
What is the significance of the zero product property in solving polynomial equations?
-The zero product property is significant in solving polynomial equations because it allows for the identification of possible solutions by setting each factor in a factored equation to zero and solving for the variable.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

POLINÔMIOS - OPERAÇÕES COM POLINÔMIOS - Professora Angela Matemática

ADIÇÃO, SUBTRAÇÃO, MULTIPLICAÇÃO e DIVISÃO | MONÔMIOS

FACTORING USING COMMON MONOMIAL FACTOR || GRADE 8 MATHEMATICS Q1

Matematika SMP - Pemfaktoran Aljabar (1) - Rumus Dasar, Rumus Jumlah dan Selisih
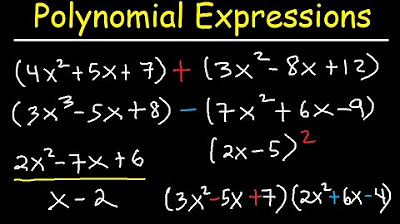
Polynomials - Adding, Subtracting, Multiplying and Dividing Algebraic Expressions

Factoring Cubic Polynomials- Algebra 2 & Precalculus
5.0 / 5 (0 votes)
