20. Recta. Determinar los puntos de intersección con los ejes.
Summary
TLDREn este video educativo, Jesús Grajeda guía a los espectadores a través del proceso de encontrar los puntos de intersección de una recta con los ejes coordenados. Utiliza la ecuación 2X + 3Y - 6 = 0 y explica paso a paso cómo sustituir valores para encontrar las intersecciones en los ejes X e Y. Finalmente, valida su solución usando GeoGebra, mostrando que la recta intersecta en los puntos (0,2) y (3,0). El video es una lección práctica y clara sobre geometría analítica.
Takeaways
- 😀 Jesús Grajeda es el presentador del video y se presenta para resolver un ejercicio sobre rectas.
- 📐 El ejercicio consiste en encontrar las intersecciones de la recta 2X + 3Y - 6 = 0 con los ejes coordenados.
- 🤔 Se explica que para encontrar los puntos de intersección, se deben considerar los ejes X e Y en el plano cartesiano.
- 📍 Se entiende que un punto de intersección tiene X = 0 (eje Y) y el otro tiene Y = 0 (eje X).
- 🧐 Se demuestra que al sustituir X = 0 en la ecuación, se obtiene la intersección con el eje Y que es (0, 2).
- 🔍 Al igual, se demuestra que al sustituir Y = 0 en la ecuación, se obtiene la intersección con el eje X que es (3, 0).
- 📝 Se resalta la importancia de la sustitución para encontrar los puntos de intersección de una recta con los ejes.
- 📊 Se utiliza GeoGebra para validar visualmente que los puntos (0, 2) y (3, 0) son correctos.
- 👍 El video es educativo y se anima a los espectadores a suscribirse y seguir en redes sociales.
- 🎓 Se enfatiza el mensaje de que las matemáticas son fundamentales y que el aprendizaje de estas es valioso.
Q & A
¿Cuál es el objetivo principal del video?
-Resolver un ejercicio matemático sobre las intersecciones de una recta con los ejes coordenados.
¿Cuál es la ecuación de la recta que se debe resolver en el ejercicio?
-La ecuación de la recta es 2X + 3Y - 6 = 0.
¿Cómo se encuentran las intersecciones de una recta con los ejes coordenados?
-Se sustituyen valores de 0 en X y en Y para encontrar los puntos de intersección con los ejes.
¿Qué sucede cuando X es igual a 0 en la ecuación?
-Cuando X es 0, se obtiene la intersección con el eje Y. Al sustituir en la ecuación, se obtiene el punto (0, 2).
¿Qué sucede cuando Y es igual a 0 en la ecuación?
-Cuando Y es 0, se obtiene la intersección con el eje X. Al sustituir en la ecuación, se obtiene el punto (3, 0).
¿Cuál es el resultado final del ejercicio?
-Las intersecciones de la recta son los puntos (0, 2) y (3, 0).
¿Cómo se valida la solución del ejercicio en el video?
-Se utiliza el software GeoGebra para graficar la recta y comprobar que cruza en los puntos (0, 2) y (3, 0).
¿Por qué es importante considerar que X vale 0 o que Y vale 0 para encontrar las intersecciones?
-Es importante porque en las intersecciones con los ejes, una de las dos coordenadas (X o Y) siempre será 0.
¿Qué recomendación da el presentador al final del video?
-El presentador recomienda suscribirse al canal y seguir sus redes sociales, recordando que 'las matemáticas te respaldan'.
¿Qué software se usa en el video para graficar la recta y validar la solución?
-Se usa GeoGebra para graficar la recta y validar los puntos de intersección.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

16. Ecuación de la recta cuando te dan dos puntos por los que pasa.

21. Encontrar la pendiente de una recta dada la ecuación general
Como ubicar puntos en el Plano Cartesiano

15. Ecuación punto-pendiente y general de la recta.
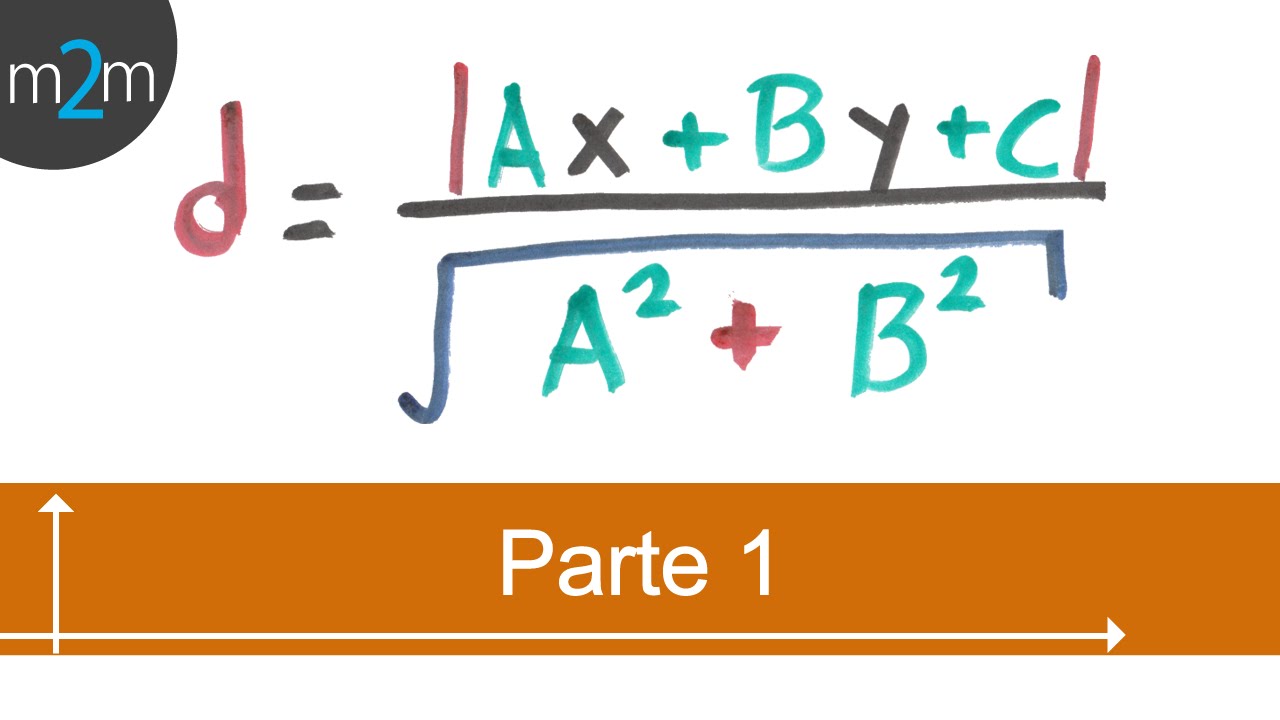
* Distancia entre un punto y una recta (PARTE 1)

Ecuación punto pendiente | Ejemplo 1
5.0 / 5 (0 votes)
