Trig functions grade 11 and 12: Horizontal stretch

Summary

In this educational video, the focus is on transforming graphs by stretching or compressing them, specifically using the sine function. The instructor explains how the coefficient in front of 'x' in a sine function affects the period of the graph. For instance, 'sin(2x)' halves the period from 360 degrees to 180 degrees, as each x-value is doubled. The tutorial demonstrates how to adjust the calculator's settings, including the step size, to accurately graph 'sin(2x)'. The instructor also covers key concepts like amplitude, range, domain, and period, providing a clear visual comparison between a standard sine graph and the transformed one.

Takeaways

• 📈 The lesson focuses on transforming graphs by stretching or compressing them, which can also be referred to as compressing.
• 🔄 In previous lessons, the movement of graphs was discussed, such as shifting a graph upwards, moving all points in the same direction.
• 🔍 The new topic is the effect of mathematical operations like '2x' on the graph of a sine function, which stretches or compresses the graph horizontally.
• 📉 When '2x' is applied to a sine function, it compresses the graph horizontally, causing it to complete its cycle in half the original period.
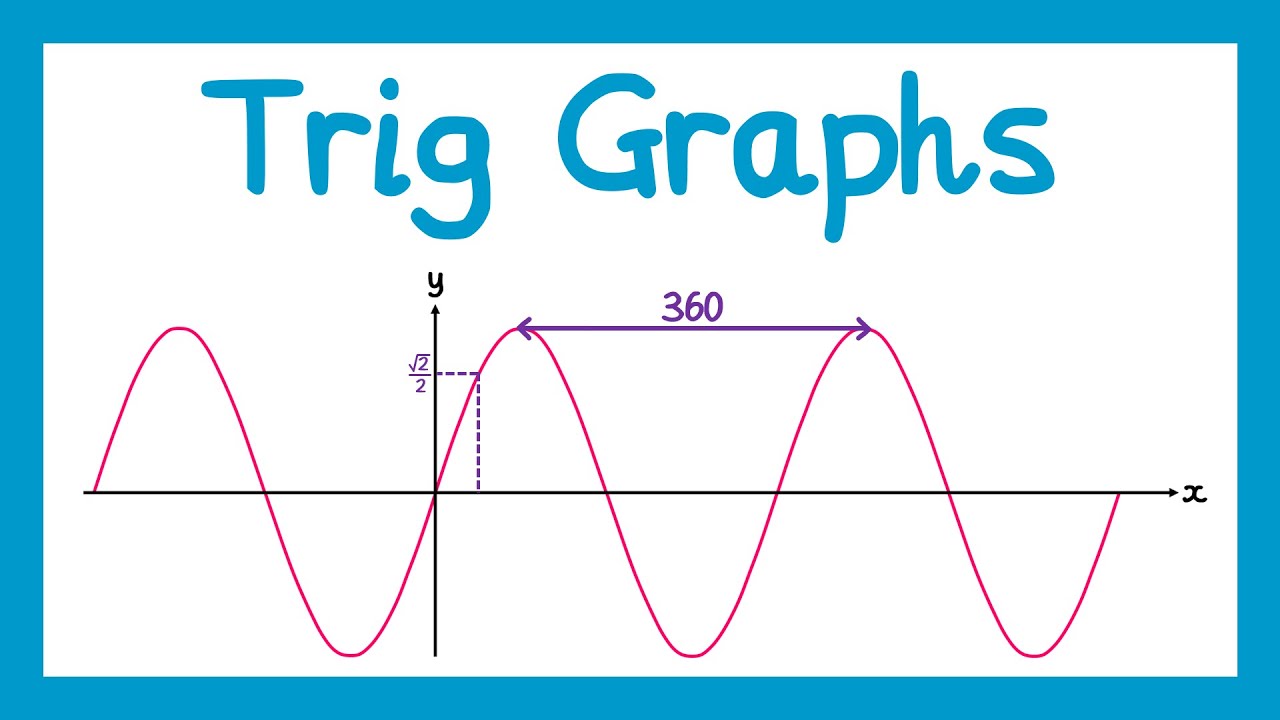
• 📋 The normal period for a sine or cosine graph is 360 degrees, but with '2x', the period becomes 180 degrees, as explained by the rule 360 divided by the coefficient of 'x'.
• 🔢 The step size on the calculator for graphing 'sin(2x)' should be set to 45 degrees, which is 180 divided by 4, to properly display the graph's shape.
• 📊 The amplitude of the 'sin(2x)' graph remains the same as the original sine graph, which is the maximum distance from the resting position (equilibrium line).
• 📐 The range of the 'sin(2x)' graph is between -1 and 1, as these are the minimum and maximum y-values of the sine function.
• 📌 The domain of the 'sin(2x)' graph is from -180 to 360, as specified in the lesson, which indicates the x-values over which the graph is drawn.
• 🔁 The 'sin(2x)' graph completes two cycles within the 360-degree range, which is a key observation for understanding the effect of '2x' on the graph.

Q & A

What is the main focus of the lesson described in the transcript?

The main focus of the lesson is to understand how graphs, specifically sine graphs, are affected when they are stretched or compressed.

What does the term 'stretching' a graph refer to in this context?

In this context, 'stretching' a graph refers to the process of enlarging the graph by altering its equation, which can result in the graph covering more space in fewer cycles.

How does the point (0, 0) on a sine graph move when the graph is stretched?

When a sine graph is stretched, the point (0, 0) would move vertically up or down depending on the nature of the stretch, but the starting point on the x-axis remains the same.

What is the effect of the term '2x' in the equation of a sine graph on the period of the graph?

The term '2x' in the equation of a sine graph halves the period of the graph. If the normal period for a sine graph is 360 degrees, with '2x', the new period becomes 180 degrees.

Why is the step size important when graphing a stretched or compressed sine function on a calculator?

The step size is important because it determines the resolution of the graph. If the step size is too large, the graph may not accurately represent the function's shape, especially after transformations like stretching or compressing.

What is the new step size for a sine graph with the equation 'sin(2x)' as compared to a standard sine graph?

For a standard sine graph, the step size is typically 90 degrees. However, for a graph with the equation 'sin(2x)', the new step size should be 45 degrees to accurately represent the halved period.

How does the amplitude of a sine graph change when the graph is stretched or compressed?

The amplitude of a sine graph does not change when the graph is stretched or compressed horizontally. The amplitude remains the maximum distance from the resting position (equilibrium line) to the peak or trough of the graph.

What is the resting position referred to in the context of a sine graph?

The resting position in the context of a sine graph refers to the equilibrium line, which is the horizontal line where the graph would be at rest, typically the x-axis.

How does the domain of a sine graph change when it is stretched or compressed?

The domain of a sine graph, which represents the set of x-values, does not change when the graph is stretched or compressed. It remains the same as specified in the problem or the original function.

What is the range of a sine graph with the equation 'sin(2x)' if the original range is between -1 and 1?

The range of a sine graph with the equation 'sin(2x)' remains between -1 and 1, as the stretching or compressing affects the period and not the amplitude.

How can you remember the rule for calculating the new period of a sine graph when the equation includes a coefficient in front of 'x'?

You can remember the rule by knowing that the period of a sine or cosine graph is always 360 degrees divided by the number in front of 'x'. So for 'sin(2x)', the new period is 360 degrees divided by 2, which equals 180 degrees.