But what is a Fourier series? From heat flow to drawing with circles | DE4
Summary
TLDRThis script delves into the mesmerizing world of complex Fourier series, where simple rotating vectors combine to create intricate shapes over time. It explores the historical context of Fourier series, originating from the heat equation, and demonstrates how these mathematical tools can describe and control complex patterns. The video explains the concept of breaking down functions into sums of sine waves and rotating vectors, leading to a deeper understanding of differential equations. It concludes by emphasizing the broad applicability of Fourier series and their significance in solving real-world problems.
Takeaways
- 📐 The video discusses the complex Fourier series, which involves adding vectors that rotate at constant frequencies to create intricate shapes over time.
- 🎭 The animation consists of 300 rotating arrows, each contributing to the complexity of the overall pattern, showcasing the beauty of mathematics in motion.
- 🔍 The complexity of the animation is contrasted with the simplicity of its components, highlighting how simple rotational motions can combine to form complex patterns.
- 🤔 The video ponders the coordination of the 'swarm' of arrows, which despite their chaotic motion, work together to trace out specific shapes.
- 🧮 Fourier series are introduced as a mathematical tool that can describe and control the complexity of such animations, emphasizing the predictability and controllability of the patterns.
- 🌡️ The origin of Fourier series is rooted in the heat equation, which Fourier developed to understand how temperature distributions evolve over time.
- 🔄 The video explains how linear equations, like the heat equation, allow for the combination of solutions to create new solutions, a fundamental property used in Fourier series.
- 🔢 The concept of infinite sums is introduced to explain how a sum of waves can approximate a discontinuous function, such as a step function, through the limit of partial sums.
- 📉 The video delves into the technicalities of Fourier series, including the computation of coefficients for the series, which are found through integrals of the function.
- 🎨 The broader view of complex functions and rotating vectors is presented as a generalization of the real-valued functions typically used in Fourier series, providing a richer context for understanding the mathematics.
Q & A
What is a complex Fourier series?
-A complex Fourier series is a mathematical technique used to decompose a function into a sum of rotating vectors, each with a constant integer frequency. It's a generalization of the more familiar Fourier series that deals with sine and cosine waves, allowing for a broader range of functions to be represented.
How does the animation with 300 rotating arrows relate to complex Fourier series?
-The animation demonstrates the concept of complex Fourier series by showing how a complex shape can be drawn over time by adding together the motion of multiple arrows, each rotating at a constant frequency. This illustrates the idea of breaking down a function into simpler, oscillatory components.
What is the significance of being able to control the initial size and angle of each vector in a complex Fourier series?
-Controlling the initial size and angle of each vector allows for the creation of a wide variety of shapes and patterns over time. This customization is essential for the practical application of Fourier series in various fields, as it enables the representation and manipulation of complex functions.
How does the concept of Fourier series relate to the heat equation?
-Fourier series is intrinsically linked to the heat equation through the work of Joseph Fourier, who developed the series to solve the heat equation. The heat equation describes how temperature distributions evolve over time, and Fourier's method of breaking down functions into simpler components allowed for the equation's solutions to be found under various initial conditions.
What is the role of linearity in the context of the heat equation and Fourier series?
-Linearity is crucial because it means that the sum of two solutions to the heat equation is also a solution, and solutions can be scaled by constants. This property allows for the construction of custom solutions by combining and scaling an infinite set of basic solutions, which are the exponentially decaying cosine waves in the context of Fourier series.
Why is the concept of infinite sums important in understanding Fourier series?
-Infinite sums are important because they allow for the representation of functions that cannot be accurately represented by finite sums alone. In the context of Fourier series, infinite sums enable the approximation of non-periodic, discontinuous, or complex functions by combining an infinite number of simpler, periodic components.
How does the concept of complex numbers and complex exponentials contribute to the understanding of Fourier series?
-Complex numbers and complex exponentials provide a powerful framework for understanding and computing Fourier series. They allow for the representation of rotating vectors and the generalization of Fourier series to functions with complex outputs, which simplifies computations and offers a deeper insight into the underlying mathematics.
What is the significance of the formula e^(i*t) in Fourier series?
-The formula e^(i*t), representing a complex exponential, is fundamental in Fourier series because it describes a point moving around the unit circle in the complex plane as time 't' progresses. This property is used to model the rotating vectors that are the building blocks of the Fourier series decomposition.
How are the coefficients in a Fourier series calculated?
-The coefficients in a Fourier series are calculated using integrals that essentially average the function over a period. For a function f(t), the coefficient c_n is found by integrating f(t) multiplied by the complex exponential e^(-i*n*2*pi*t) over the interval [0, 1], and then multiplying by the appropriate normalizing factor.
What is the practical application of Fourier series in solving differential equations?
-Fourier series are used to solve differential equations by expressing complex functions as a sum of simpler, exponential functions. This allows for the application of linearity properties and the superposition principle, enabling the construction of solutions for a wide range of initial conditions and boundary conditions.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes
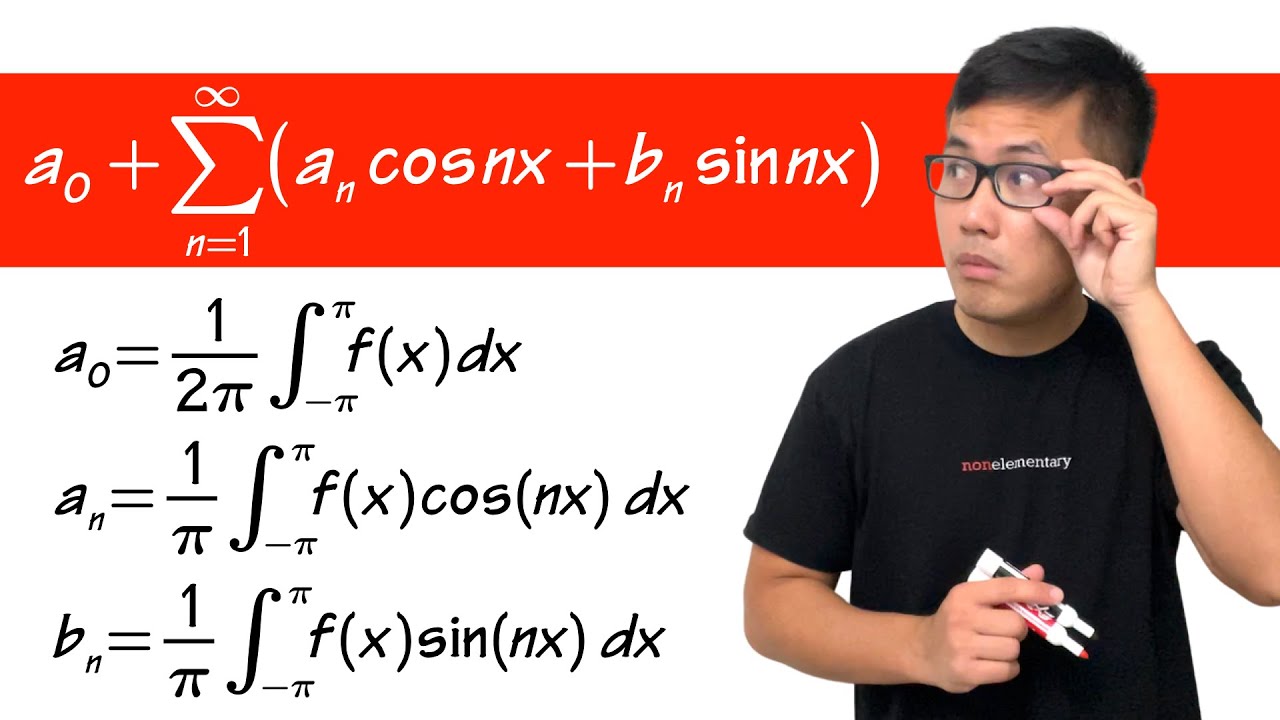
how to get the Fourier series coefficients (fourier series engineering mathematics)

The Fourier Series and Fourier Transform Demystified

How does a fan work ? | Single phase induction motor

What is Continuous Wavelet Transform (CWT)? | Wavelet Theory | Advanced Digital Signal Processing

Give Me 7min, and I’ll improve your drawing skills by 176%
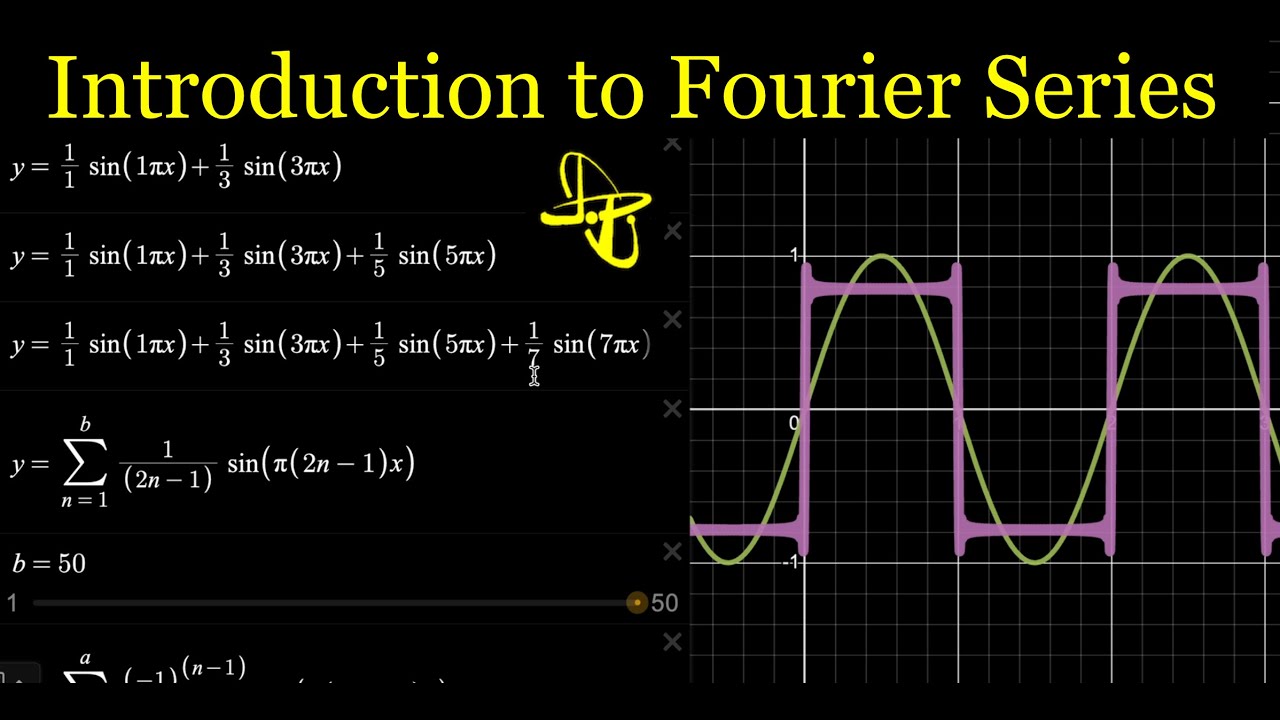
Introduction to Fourier Series - Adding Sine Waves to make Sawtooth, Square, and Triangle Waves
5.0 / 5 (0 votes)
