A Level Physics Revision: All of Capacitors (in under 21 minutes)
Summary
TLDRThis A-Level physics tutorial explores the fundamentals of capacitors, including their symbol, function, and the concept of capacitance. It explains how capacitors store electrical charge proportional to potential difference and introduces the formula for capacitance (C = Q/V). The tutorial covers charging and discharging processes, the role of electron flow, and how capacitors can serve as a power source. It also delves into series and parallel configurations, explaining the rules for calculating total capacitance in each case. The video further discusses the exponential nature of voltage and current changes during charging and discharging, introduces the time constant, and demonstrates how to derive it from graphs. Practical examples and calculations are provided to solidify understanding.
Takeaways
- 🔋 The symbol for a capacitor is two parallel lines, representing its function to store electrical charge.
- 🔌 Capacitors charge and discharge in a circuit, storing charge when connected to a power supply and releasing it when connected to a load like a light bulb.
- ⚡ The amount of charge a capacitor can store is proportional to the potential difference across it, with the constant of proportionality being the capacitance (C).
- ⚖️ Capacitance is defined as the amount of charge stored per unit of potential difference, measured in farads (F), where 1 F = 1 coulomb per volt.
- 🔄 When charging, electrons flow from the negative terminal of the power source to the negative plate of the capacitor, creating an equal and opposite charge on the positive plate.
- 🔌 In a parallel circuit with capacitors, the total capacitance (C_total) is the sum of individual capacitances (C1 + C2), and the voltage across all is the same.
- 🔗 In a series circuit with capacitors, the total capacitance is found using the reciprocal formula: 1/C_total = 1/C1 + 1/C2, and each capacitor experiences the same current.
- 📉 The voltage, current, and charge in a discharging capacitor decrease exponentially over time, following the formula V = V_initial * e^(-t/(CR)).
- 🕒 The time constant (τ) of a capacitor is the product of its capacitance and the resistance in the circuit, and it determines the rate of charge/discharge.
- 📈 The time constant can be determined from a graph of voltage, current, or charge over time, where the voltage drops to approximately 37% of its initial value after one time constant.
- 🔌 During charging, the voltage across a capacitor increases exponentially while the voltage across a resistor in series decreases, with the total voltage remaining constant due to Kirchhoff's second law.
Q & A
What is the symbol for a capacitor?
-The symbol for a capacitor is two parallel lines.
What is the fundamental purpose of a capacitor?
-The fundamental purpose of a capacitor is to store electrical charge.
How is the amount of charge stored on a capacitor related to the potential difference across it?
-The amount of charge stored on a capacitor is proportional to the potential difference across it.
What is the constant of proportionality between the charge and potential difference on a capacitor called?
-The constant of proportionality between the charge and potential difference on a capacitor is called capacitance, symbolized by 'C'.
What is the unit of capacitance and how is one farad defined?
-The unit of capacitance is the farad. One farad is defined as the amount of capacitance when one coulomb of charge is stored for one volt.
How can the charging of a capacitor be explained in terms of electron flow?
-During the charging of a capacitor, electrons flow from the negative terminal of the cell to the negative plate of the capacitor, causing excess electrons to gather on the negative plate and repelling electrons from the positive plate, leading to an equal and opposite charge on the plates.
How does the total capacitance change when capacitors are connected in parallel?
-When capacitors are connected in parallel, the total capacitance is the algebraic sum of the individual capacitances, expressed as C_total = C1 + C2.
What is the rule for calculating the total capacitance when capacitors are connected in series?
-For capacitors in series, the total capacitance C_total is calculated as the reciprocal of the sum of the reciprocals of the individual capacitances: 1/C_total = 1/C1 + 1/C2.
Why is the potential difference the same across all capacitors in a parallel circuit?
-In a parallel circuit, the potential difference is the same across all branches because the voltage of the source (e.g., a cell) is distributed equally across all parallel paths.
How is the charge shared in a parallel circuit with capacitors?
-In a parallel circuit, the total charge is shared among the capacitors, with the total charge Q_total being the sum of the individual charges Q1 + Q2.
What is the time constant in the context of capacitors, and how is it defined?
-The time constant, denoted by the Greek letter tau (τ), is the product of the capacitance and resistance in a circuit. It represents the time it takes for the voltage (or current) to reach approximately 37% of its final value during the charging or discharging of a capacitor.
How does the voltage across a discharging capacitor decrease over time?
-The voltage across a discharging capacitor decreases exponentially over time following the formula V = V_0 * e^(-t/(CR)), where V_0 is the initial voltage, t is the time, C is the capacitance, and R is the resistance.
What happens to the potential difference, charge, and current at time equals the time constant during capacitor discharge?
-At time equals the time constant, the potential difference, charge, and current will drop to approximately 37% of their initial values during the discharge of a capacitor.
How can the capacitance of a capacitor be determined from a discharge graph?
-The capacitance can be determined from a discharge graph by identifying the time constant from the graph, which is the time it takes for the voltage to drop to 37% of its initial value, and then dividing this time by the resistance in the circuit.
What is the relationship between the potential difference across a charging capacitor and the time since it started charging?
-The potential difference across a charging capacitor increases with time, following the formula V_C = V_0 * (1 - e^(-t/(CR))), where V_0 is the initial potential difference, t is the time, C is the capacitance, and R is the resistance.
How does the current in a series circuit change as a capacitor charges?
-As the capacitor charges in a series circuit, the current decreases exponentially over time, following the same formula as the potential difference across the resistor: I = I_0 * e^(-t/(CR)), where I_0 is the initial current.
Outlines

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantMindmap

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantKeywords

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantHighlights

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantTranscripts

Cette section est réservée aux utilisateurs payants. Améliorez votre compte pour accéder à cette section.
Améliorer maintenantVoir Plus de Vidéos Connexes

Capacitor Explained : Calculations | Series | Parallel | Charging | Discharging
Lab Virtual : Kapasitor Keping Sejajar | Kapasitansi | Phet Simulation | Fisika Kelas XII

Kapasitor, Simulasi Phet, Fisika kelas XII
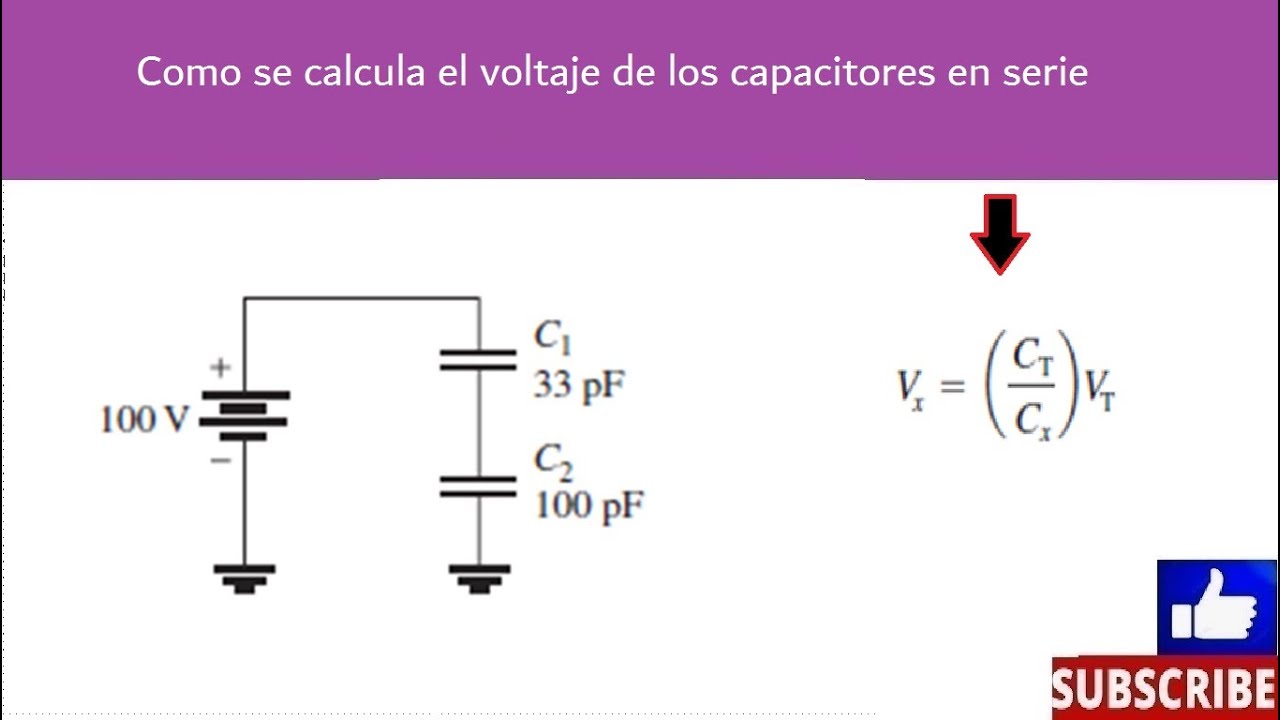
Voltaje de capacitores en serie

Voltage, Electric Energy, and Capacitors: Crash Course Physics #27
Potensial Listrik dan Kapasitor
5.0 / 5 (0 votes)
