Productos Notables | Binomio Conjugado | Suma por diferencia | Ejemplo 2
Summary
TLDREn este vídeo, el instructor presenta el concepto de binomio conjugado y cómo aplicarlo en el producto de la suma por la diferencia. Seguidamente, resuelve ejemplos donde se demuestra el proceso paso a paso, destacando la importancia de que los términos dentro de los paréntesis sean iguales excepto por el signo. Finalmente, invita a los estudiantes a practicar con ejercicios similares y a explorar el curso completo de productos notables en su canal.
Takeaways
- 📚 Este es un curso sobre productos notables, específicamente sobre el binomio conjugado y el producto de la suma por la diferencia.
- 🔍 Se enfatiza la importancia de observar que los dos paréntesis deben tener términos iguales, excepto por el signo, para aplicar el binomio conjugado.
- 📘 Se recomienda revisar el video anterior si los ejercicios parecen difíciles, ya que explica la fórmula y su aplicación.
- 🔢 El binomio conjugado se resuelve siempre que los paréntesis tengan términos iguales, uno con signo positivo y otro con signo negativo.
- ✅ La fórmula para resolver es (primero)^2 - (segundo)^2, donde 'primero' y 'segundo' son los términos dentro de los paréntesis.
- 📝 En el primer ejercicio, se resuelve utilizando el binomio conjugado, identificando correctamente los términos y elevándolos al cuadrado.
- 📉 El primer término del primer ejercicio es (4x)^2 y el segundo término es (8y^3)^2, siguiendo la fórmula mencionada.
- 📈 En el segundo ejercicio, se identifican los términos (1/2m^5) y (3/4n^3), y se elevan al cuadrado siguiendo la misma técnica.
- 📚 Se menciona la importancia de entender las propiedades de la potenciación, especialmente cuando hay fracciones.
- 📝 Se ofrecen ejercicios adicionales para que los estudiantes practiquen y apliquen lo aprendido.
- 👍 El instructor anima a los estudiantes a suscribirse, comentar, compartir y dar 'me gusta' al video para seguir aprendiendo.
Q & A
¿Qué es un binomio conjugado y cómo se relaciona con los productos notables?
-Un binomio conjugado es una expresión que consta de dos términos iguales excepto por el signo. Se relaciona con los productos notables porque se utiliza para resolver sumas y diferencias de cuadrados de binomios, como se muestra en el ejemplo del script.
¿Cómo se identifica si un problema puede ser resuelto utilizando el binomio conjugado?
-Para resolver un problema utilizando el binomio conjugado, se debe observar que hay dos paréntesis con términos iguales excepto por el signo. Si hay un cambio en los términos, como un término cuadrado y otro en el cubo, no se puede resolver por este método.
¿Cuál es la fórmula para resolver un producto de conjugado o la suma por la diferencia?
-La fórmula para resolver un producto de conjugado o la suma por la diferencia es (primer término) al cuadrado menos (segundo término) al cuadrado. Esto se aplica siempre que los términos sean iguales excepto por el signo.
¿Cómo se calcula (4x^2 + 8)(4x^2 - 8) según el script?
-Según el script, se calcula elevando al cuadrado el primer término (4x^2)^2, que resulta en 16x^4, y luego elevando al cuadrado el segundo término (8)^2, que resulta en 64, y finalmente se resta el segundo resultado del primero.
¿Qué significa 'todo igual excepto el signo' en el contexto de los productos notables?
-En el contexto de los productos notables, 'todo igual excepto el signo' significa que los dos términos del binomio deben ser idénticos en valor, pero uno debe ser positivo y el otro negativo para aplicar el binomio conjugado.
¿Cómo se manejan las potencias en la resolución de productos notables?
-Cuando se resuelven productos notables con potencias, se aplican las propiedades de la potenciación. Por ejemplo, si hay un producto elevado a un exponente, ese exponente se coloca sobre cada uno de los factores del producto.
¿Cómo se calcula (1/2m + 3/4n^3)(1/2m - 3/4n^3) según el script?
-Según el script, se calcula elevando al cuadrado el primer término (1/2m)^2, que resulta en 1/4m^2, y luego elevando al cuadrado el segundo término (3/4n^3)^2, que resulta en 9/16n^6, y finalmente se resta el segundo resultado del primero.
¿Qué es la propiedad de potenciación que se menciona en el script para el ejemplo con fracciones?
-La propiedad de potenciación mencionada en el script indica que cuando hay una fracción elevada a un exponente, ese exponente se aplica tanto al numerador como al denominador de la fracción.
¿Cuáles son los dos ejercicios adicionales que se sugieren para práctica en el script?
-Los dos ejercicios adicionales son: (5 + 6x^3)(5 - 6x^3) y (3/4m + 3/4n^3)(3/4m - 3/4n^3). Se espera que el espectador practique estos ejercicios utilizando la técnica de los productos notables.
¿Cómo se resuelve el primer ejercicio adicional (5 + 6x^3)(5 - 6x^3) según el script?
-Según el script, se resuelve aplicando la fórmula del binomio conjugado: (5)^2 - (6x^3)^2, lo que resulta en 25 - 36x^6.
¿Cómo se resuelve el segundo ejercicio adicional (3/4m + 3/4n^3)(3/4m - 3/4n^3) según el script?
-Según el script, se resuelve de la misma manera que el ejercicio anterior, pero con los términos dados: (3/4m)^2 - (3/4n^3)^2, lo que resulta en 9/16m^2 - 9/16n^6.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Matemáticas I: Video 2 7 1

PRODUCTOS NOTABLES: Suma y resta de un binomio al cuadrado. Producto de dos binomios conjugados

Producto de la suma por la diferencia |Binomio conjugado |PRODUCTOS NOTABLES

Límites por racionalización 1
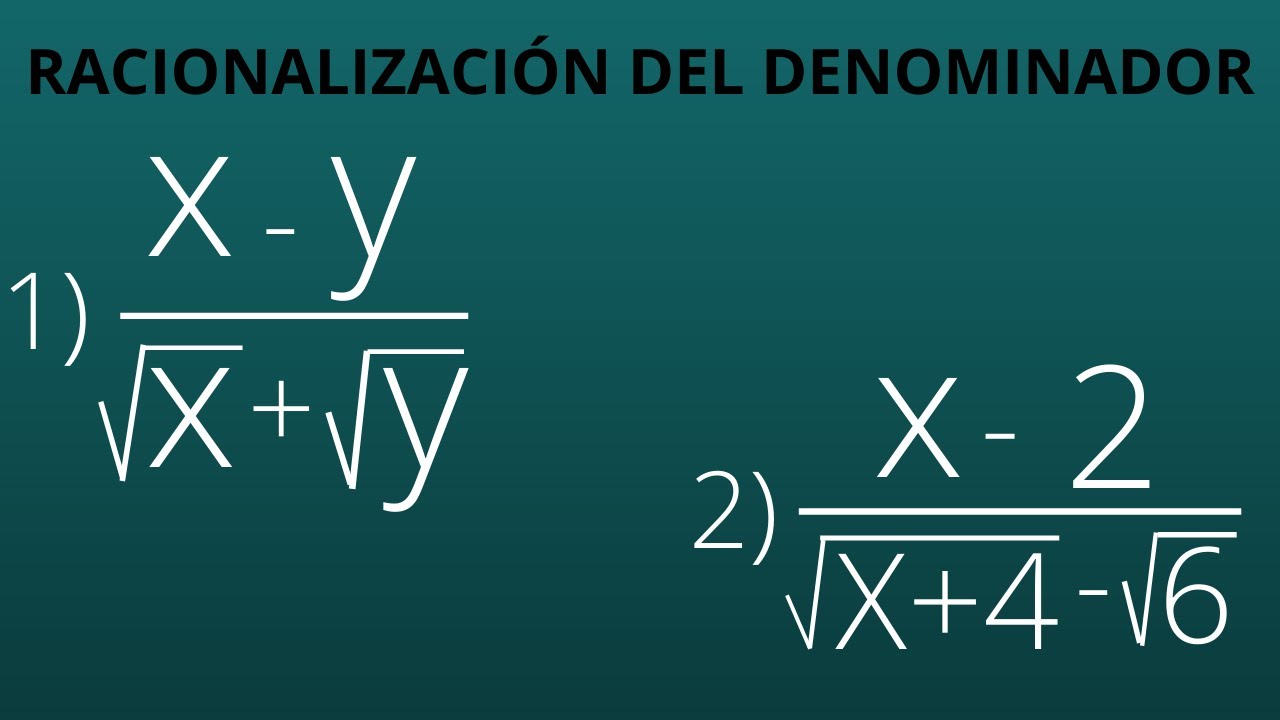
Racionalización del denominador (binomio) con expresiones algebraicas, explicado paso a paso.

Lenguaje algebraico | Parte 2

Producto de binomios conjugados | Ejemplo 1 Principiantes
5.0 / 5 (0 votes)