RAZON DE CAMBIO PROMEDIO DE UNA FUNCION. Explicación Detallada Paso a Paso
Summary
TLDREste video introduce el concepto de razón de cambio promedio de una función, un tema crucial antes de abordar las derivadas en cálculo diferencial. Se explica cómo las variables de una función cambian y cómo se calcula la razón de cambio promedio usando la diferencia entre dos puntos en la función. El video desglosa estos conceptos de manera accesible, preparando al espectador para futuros temas más complejos como las derivadas, utilizando ejemplos sencillos y una explicación paso a paso. Se destaca la importancia de este concepto en la comprensión del cambio en funciones matemáticas.
Takeaways
- 📚 El video trata sobre el concepto de razón de cambio promedio de una función en el contexto del cálculo diferencial.
- 🔍 Se analiza cómo cambia una función cuando sus variables cambian, específicamente entre dos puntos, x1 y x2.
- 📐 Se introduce el término 'delta x' (Δx) para representar el cambio o incremento en la variable x entre dos puntos.
- 📈 El 'incremento en y' (Δy) es el cambio en la función correspondiente al cambio en x, y se calcula como f(x2) - f(x1).
- 🧩 La razón de cambio promedio de una función f(x) se define como el incremento en y dividido por el incremento en x, es decir, Δy/Δx.
- 📝 Se describe el proceso para calcular el valor de x2 a partir de un incremento de x, utilizando la fórmula x2 = x1 + Δx.
- 🔢 Se muestra cómo reescribir la razón de cambio promedio de f(x) en términos de los valores de x y Δx.
- 📉 La fórmula final para la razón de cambio promedio es f(x + Δx) - f(x) / Δx, lo que indica cómo la función cambia con el cambio en x.
- 🤔 Se menciona que esta expresión no es una derivada, pero está relacionada y se explorará más adelante en el contexto de límites.
- 👍 Se anima a los espectadores a suscribirse y a dejar comentarios si tienen dudas, prometiendo más contenido en futuras videos.
- 👋 El video termina con un saludo y una promesa de volver con más información en un próximo video.
Q & A
¿Qué es la razón de cambio promedio de una función?
-La razón de cambio promedio de una función es una medida de cómo cambia una función cuando sus variables cambian. Se expresa como la razón entre el incremento en el valor de la función (Δy) y el incremento en la variable independiente (Δx).
¿Cómo se define el cambio o incremento en la variable x?
-El cambio o incremento en la variable x, denotado como Δx, es la diferencia entre dos valores de x, es decir, x2 - x1.
¿Qué representa el incremento en la variable y, conocido como Δy?
-El incremento en la variable y, representado por Δy, es la diferencia entre los valores de la función en dos puntos diferentes, f(x2) - f(x1).
¿Cómo se calcula la razón de cambio promedio de una función f(x)?
-La razón de cambio promedio de la función f(x) se calcula dividiendo el incremento en y (Δy) entre el incremento en x (Δx), es decir, (Δy / Δx) = (f(x2) - f(x1)) / (x2 - x1).
¿Por qué es importante entender la razón de cambio promedio en el cálculo diferencial?
-La razón de cambio promedio es fundamental en el cálculo diferencial porque es una aproximación del cambio que experimenta una función cuando sus variables cambian, y es una herramienta para entender cómo se comporta la función en un intervalo específico.
¿Cómo se relaciona la razón de cambio promedio con la derivada de una función?
-La razón de cambio promedio es una aproximación de la derivada de una función. A medida que el intervalo entre x1 y x2 se vuelve más pequeño, la razón de cambio promedio se acerca más a la derivada de la función en el punto x.
¿Qué es el límite y cómo se relaciona con la derivada y la razón de cambio promedio?
-El límite es un concepto matemático que describe el comportamiento de una función cuando el valor de la variable se acerca a un límite determinado. La derivada de una función se define como el límite de la razón de cambio promedio cuando Δx se acerca a cero.
¿Cómo se puede simplificar la fórmula de la razón de cambio promedio cuando se conoce el valor de x2?
-Cuando se conoce el valor de x2, la fórmula de la razón de cambio promedio se simplifica sustituyendo x2 por x1 + Δx, lo que nos da (f(x1 + Δx) - f(x1)) / Δx.
¿Qué significa el término 'incremento' en el contexto de la razón de cambio promedio?
-El término 'incremento' en el contexto de la razón de cambio promedio no necesariamente se refiere a un aumento; puede ser tanto un aumento como una disminución en la variable o el valor de la función.
¿Cómo se relaciona la razón de cambio promedio con la velocidad en el ejemplo dado del objeto en movimiento?
-La razón de cambio promedio se relaciona con la velocidad porque, al igual que la velocidad es una razón entre la distancia recorrida y el tiempo transcurrido, la razón de cambio promedio es una razón entre el cambio en la función y el cambio en la variable independiente.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Razón de cambio promedio e instantaneo

QUÉ ES EL CÁLCULO DIFERENCIAL. Explicación Básica.

Concepto de diferencial - Infinitésimos

Tasa de variación media.

LA DERIVADA COMO RAZÓN de CAMBIO (EXPLICACIÓN y DEFINICIÓN) - #1
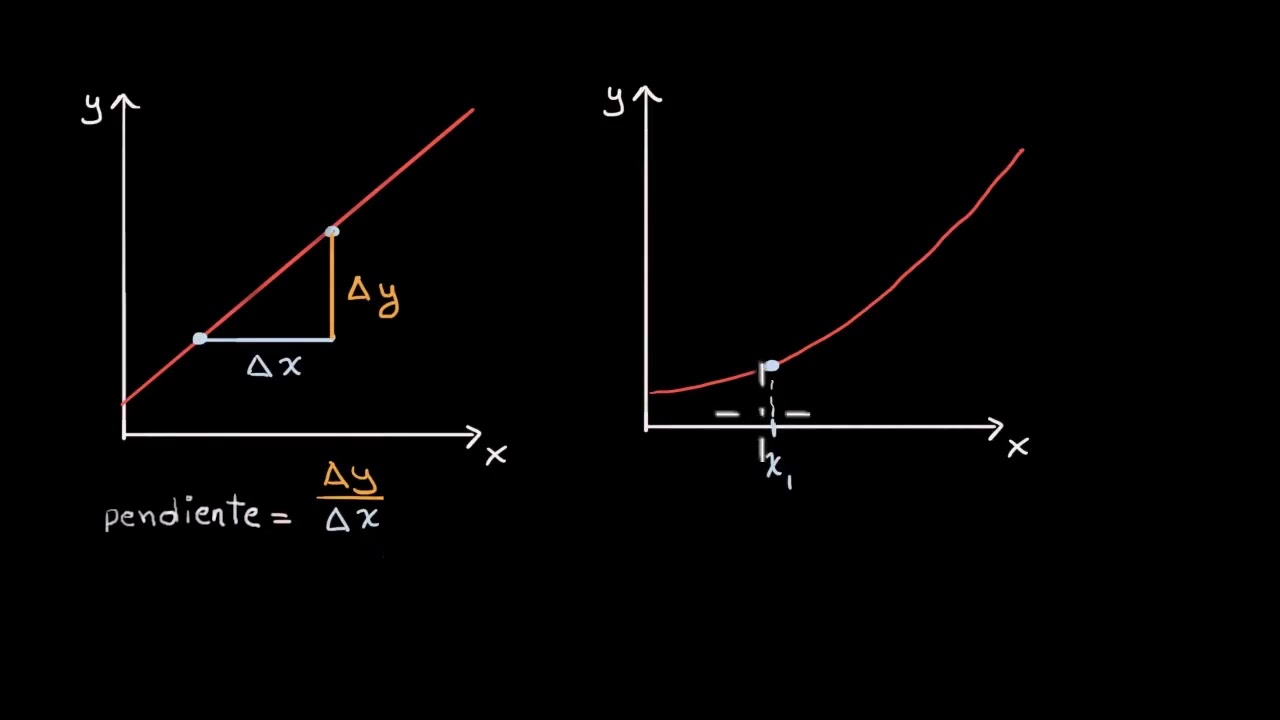
El concepto de derivada | Khan Academy en Español

Diferencial de una función en un punto. ¿Qué es y para qué sirve? BACHILLERATO MATEMÁTICAS
5.0 / 5 (0 votes)