4 Método Gráfico y tabular
Summary
TLDREn este video, se utiliza el método tabular y gráfico para resolver sistemas de ecuaciones lineales. Se recomienda renombrar las ecuaciones y despejar una variable, como 'g', para encontrar la intersección de las rectas. Se sugiere analizar si las rectas se cortan y trazar puntos para identificar la intersección, como en el caso de los puntos (6,2). Es importante recordar que para una recta, se necesitan dos puntos.
Takeaways
- 📚 El video enseña cómo resolver sistemas de ecuaciones lineales utilizando el método tabular y gráfico.
- 🔍 Se recomienda renombrar las ecuaciones y despejar una variable, en este caso 'g', para facilitar el proceso.
- ✍️ La primera ecuación se despeja para que 'y' sea igual a '8x'.
- 📐 La segunda ecuación se despeja para que 'y' sea 'x - 4'.
- 🤔 Se debe tener en cuenta que este método es útil si hay certeza de que las rectas se cruzan, es decir, no son paralelas ni una es múltiplo de la otra.
- 🔢 Se utiliza un rango de valores de 0 hasta 6 para analizar las intersecciones.
- 📈 Se sustituyen los valores en las ecuaciones correspondientes para encontrar los puntos de intersección.
- 📍 Se determina que cuando 'x' vale 6, ambas ecuaciones dan un 'y' de 2, indicando un punto de intersección en (6, 2).
- 📊 Al graficar los puntos, se identifican los puntos de intersección visualmente, donde los puntos en azul y rojo coinciden.
- 📌 El punto de intersección confirmado es (6, 2), que es el punto donde ambas rectas se cruzan.
Q & A
¿Qué método se utiliza en el video para resolver sistemas de ecuaciones lineales?
-Se utiliza el método tabular y gráfico para resolver sistemas de ecuaciones lineales.
¿Cuál es la primera acción a realizar en el proceso descrito en el video?
-La primera acción es renombrar cada una de las ecuaciones y despejar cada una de ellas en términos de 'g'.
¿Qué significa despejar una ecuación en términos de 'g'?
-Despejar una ecuación en términos de 'g' significa aislar la variable 'g' en cada ecuación para poder resolver el sistema.
¿Por qué es importante despejar las ecuaciones en términos de 'g'?
-Es importante para poder encontrar los valores de 'g' que satisfacen ambas ecuaciones, lo que nos dará el punto de intersección de las rectas representadas por estas ecuaciones.
¿Qué condiciones deben cumplir las rectas para que el método descrito en el video sea aplicable?
-Las rectas deben poderse cortar, es decir, no pueden ser paralelas ni una ser múltiplo de la otra, ya que en esos casos no se encontraría un punto de intersección.
¿Cuál es el rango de valores que se considera en el ejemplo del video?
-Se considera el rango de 0 hasta 6 para los valores de 'x'.
¿Cómo se determinan los valores de 'g' en el ejemplo del video?
-Se determinan sustituyendo los valores de 'x' en las ecuaciones correspondientes y encontrando los valores de 'g' que satisfacen ambas ecuaciones.
¿Cuál es el punto de intersección que se encuentra en el ejemplo del video?
-El punto de intersección encontrado es (6, 2), ya que para 'x' igual a 6, ambas ecuaciones dan un valor de 'g' igual a 2.
¿Cómo se representa gráficamente el punto de intersección en el video?
-Se representan gráficamente los puntos que satisfacen cada ecuación, y se identifica el punto de intersección como el punto en el que las rectas se cortan, en este caso, el punto (6, 2).
¿Qué se debe recordar para que se pueda trazar una recta correctamente en este método?
-Se debe recordar que para trazar una recta se necesitan dos puntos, y en este caso, se utilizan los puntos que se obtienen al sustituir los valores de 'x' en las ecuaciones.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
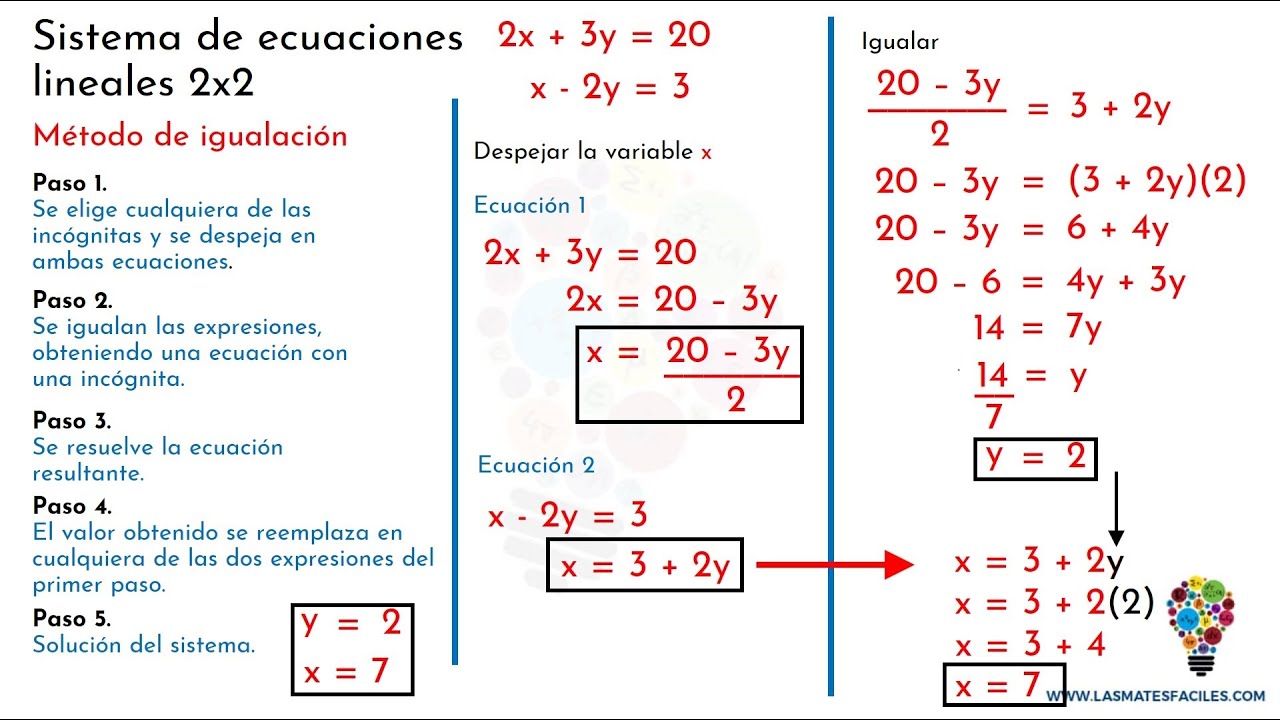
Sistemas de Ecuaciones 2x2 - Método de Igualación

Sistemas de ecuaciones | Solución Método Gráfico | Ejemplo 2

09. ¿Qué es un sistema de ecuaciones lineales con dos incógnitas?

Sistemas de ecuaciones lineales 2x2 INTRODUCCIÓN

01. Sistemas de ecuaciones lineales, 2 variables | Álgebra Lineal

Resolviendo sistemas lineales por el método gráfico
5.0 / 5 (0 votes)