Coefficient of static Friction || block and horizontal surface #11thphysics @a2zpractical991
Summary
TLDRThe transcript requests a correction in the slope calculation formula, emphasizing the correct formula as 'y2-y1/x2-x1' and provides a specific slope value of '4÷19' which simplifies to 0.21. It also instructs to adjust the coefficient of static friction according to a graph, aligning it with the calculated slope value. This concise correction highlights the importance of accurate mathematical representation and its application in understanding physical phenomena.
Takeaways
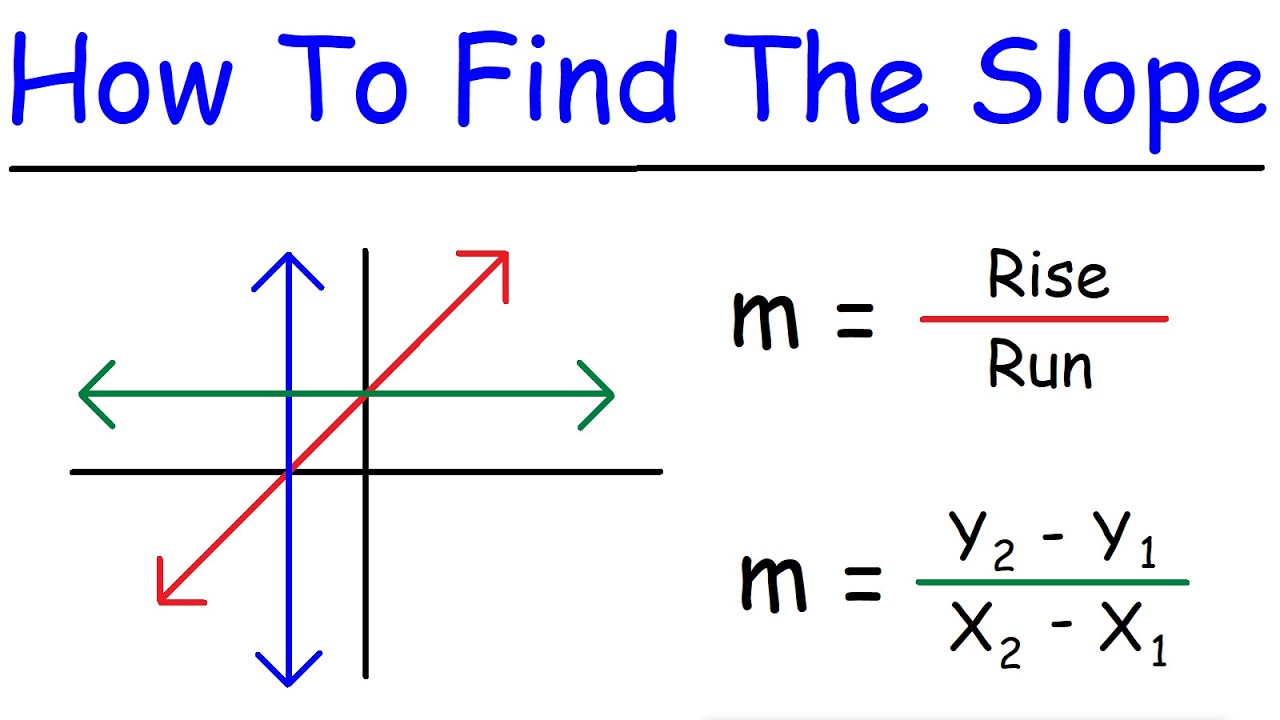
- 📐 The slope formula is corrected to \( \frac{y2 - y1}{x2 - x1} \).
- 🔢 The corrected calculation of the slope results in a value of 0.21.
- 📊 The coefficient of static friction is adjusted to match the graph's indication, which is 0.21.
- ✅ The importance of accurate calculations in physics is emphasized for precise results.
- 📈 Understanding the relationship between the slope of a line and the coefficient of static friction is crucial.
- 📚 The correction process highlights the need for careful review of mathematical expressions.
- 🔍 The graph serves as a visual tool to verify and correct the numerical values in physics problems.
- 🧲 Static friction plays a significant role in understanding the forces at play in various scenarios.
- 🔧 The correction of the coefficient of static friction is essential for accurate physical models.
- 📝 It's important to double-check calculations and use visual aids like graphs for verification.
- 🌐 The process of correcting mathematical expressions and coefficients is a common practice in scientific research.
Q & A
What is the formula for calculating the slope of a line?
-The slope of a line is calculated using the formula \( \frac{y2 - y1}{x2 - x1} \), where \( y1 \) and \( y2 \) are the y-coordinates of two points on the line, and \( x1 \) and \( x2 \) are the corresponding x-coordinates.
What was the error in the original slope calculation mentioned in the transcript?
-The error was in the division of the slope formula, which was corrected to 4 divided by 19, resulting in a slope of 0.21.
What is the significance of the slope value in the context of the transcript?
-The slope value of 0.21 is significant as it is used to correct the coefficient of static friction in the graph, indicating the relationship between frictional force and the normal force.
How does the coefficient of static friction relate to the slope of the graph?
-The coefficient of static friction is represented graphically as the slope of the line in the force-displacement diagram, where the slope indicates the ratio of frictional force to the normal force.
What is the corrected coefficient of static friction according to the transcript?
-The corrected coefficient of static friction is 0.21, as derived from the corrected slope calculation.
Why is it important to correct the calculations in scientific analysis?
-Correct calculations are crucial in scientific analysis to ensure accuracy and validity of the results, which can affect conclusions and subsequent research or applications.
What could be the implications of an incorrect coefficient of static friction in engineering or physics?
-An incorrect coefficient of static friction could lead to inaccurate predictions in friction-related phenomena, potentially affecting the design and safety of mechanical systems.
How can one verify the correctness of the slope calculation?
-One can verify the correctness of the slope calculation by using the correct formula and substituting the appropriate values, then comparing the result with the expected or calculated value.
What is the role of a graph in visualizing the relationship between variables?
-A graph plays a crucial role in visualizing the relationship between variables by providing a visual representation of data points and trends, making it easier to understand complex relationships and patterns.
What are some common mistakes made when calculating the slope of a line?
-Common mistakes include using incorrect values for \( x1 \), \( y1 \), \( x2 \), and \( y2 \), or misapplying the slope formula, which can lead to erroneous results.
How can one improve their understanding of the slope formula and its applications?
-One can improve their understanding by practicing with various examples, reviewing related concepts in geometry and algebra, and applying the formula in different real-world scenarios.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Distance Formula | Introduction to Analytic Geometry|
How To Find The Slope of a Line | Algebra

GCSE Maths - How to Find the Gradient Using the Coordinates of Two Points #66

Average vs Instantaneous Rates of Change

Distancia entre dos puntos | Demostración de la fórmula

Pengertian Kemiringan Hal 235-238 Bab 5 Persamaan Garis Lurus Kelas 8 Kurikulum Merdeka Belajar
5.0 / 5 (0 votes)
