Pola Bilangan (5) | Barisan dan Deret Geometri
Summary
TLDRIn this video, the host explains key concepts in mathematics, specifically focusing on geometric sequences and series for 8th-grade students. The video covers how to identify geometric sequences by finding their common ratio and how to apply formulas to determine the nth term (Un) of a geometric sequence. It also explores the concept of geometric series and demonstrates how to calculate the sum of the first n terms using specific formulas. Through practical examples, the host walks viewers through solving problems involving geometric sequences and series, making complex mathematical concepts easier to understand.
Takeaways
- 😀 Geometric sequences are patterns of numbers where each term is multiplied by a fixed ratio to get the next term.
- 😀 The ratio (r) in a geometric sequence is the constant factor between consecutive terms. It can be calculated by dividing a term by its previous term.
- 😀 To determine if a sequence is geometric, divide consecutive terms and check if the ratio remains constant.
- 😀 Example 1: In the sequence 1, 3, 9, 27, the ratio is 3, which makes it a geometric sequence.
- 😀 Example 2: In the sequence 120, -60, 30, 15, the ratio is 1/2, which makes it a geometric sequence as well.
- 😀 The formula for the nth term (Un) of a geometric sequence is Un = a * r^(n-1), where 'a' is the first term and 'r' is the common ratio.
- 😀 To find the 10th term of a geometric sequence, simply apply the formula for Un with appropriate values for 'a', 'r', and 'n'.
- 😀 Example: For the sequence 1, 3, 9, 27, the 10th term (U10) is 19683, calculated using the formula with 'a' = 1 and 'r' = 3.
- 😀 A geometric series (or sum) is the sum of terms from a geometric sequence, and it can be calculated using a specific formula depending on the ratio.
- 😀 If the ratio is greater than 1, use the formula SN = a * (r^n - 1) / (r - 1) for the sum of the first n terms. If the ratio is less than 1, use SN = a * (1 - r^n) / (1 - r).
Q & A
What is a geometric sequence?
-A geometric sequence is a series of numbers where each term after the first is found by multiplying the previous term by a fixed, non-zero number called the ratio.
How do you determine if a sequence is a geometric sequence?
-To determine if a sequence is a geometric sequence, divide each term by its preceding term. If the ratio remains constant for all consecutive terms, then it is a geometric sequence.
What is the ratio in a geometric sequence?
-The ratio in a geometric sequence is the constant number that each term is multiplied by to get the next term. It is denoted by 'r'.
Can you give an example of a geometric sequence?
-Sure! An example of a geometric sequence is 1, 3, 9, 27, ..., where each term is multiplied by 3 to get the next term.
What is the formula to find the nth term of a geometric sequence?
-The formula to find the nth term (Un) of a geometric sequence is: Un = a * r^(n-1), where 'a' is the first term, 'r' is the common ratio, and 'n' is the position of the term.
How do you calculate the 10th term of the sequence 1, 3, 9, 27, ...?
-To calculate the 10th term, use the formula Un = a * r^(n-1). Here, a = 1, r = 3, and n = 10. So, U10 = 1 * 3^(10-1) = 3^9 = 19683.
What is a geometric series?
-A geometric series is the sum of the terms of a geometric sequence. It is denoted as S_n, the sum of the first n terms.
How do you find the sum of the first 9 terms of the geometric sequence 1, 3, 9, 27, ...?
-The sum of the first 9 terms can be found using the formula for the sum of a geometric series: S_n = a * (r^n - 1) / (r - 1). For the sequence 1, 3, 9, 27, ..., we get S9 = 1 * (3^9 - 1) / (3 - 1) = 9841.
What happens if the ratio 'r' is less than 1 in a geometric series?
-If the ratio 'r' is less than 1 but greater than 0, the terms of the geometric series decrease and approach zero. The sum of such a series can be calculated using the formula: S_n = a * (1 - r^n) / (1 - r).
How do you find the sum of the first 6 terms of the sequence 120, -60, 30, 15, ...?
-To find the sum of the first 6 terms, we use the formula for the sum of a geometric series: S_n = a * (1 - r^n) / (1 - r). Here, a = 120, r = -1/2, and n = 6. So, S6 = 120 * (1 - (-1/2)^6) / (1 - (-1/2)) = 236.25.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Pola Bilangan [Part 1] - Mengenal Pola Bilangan
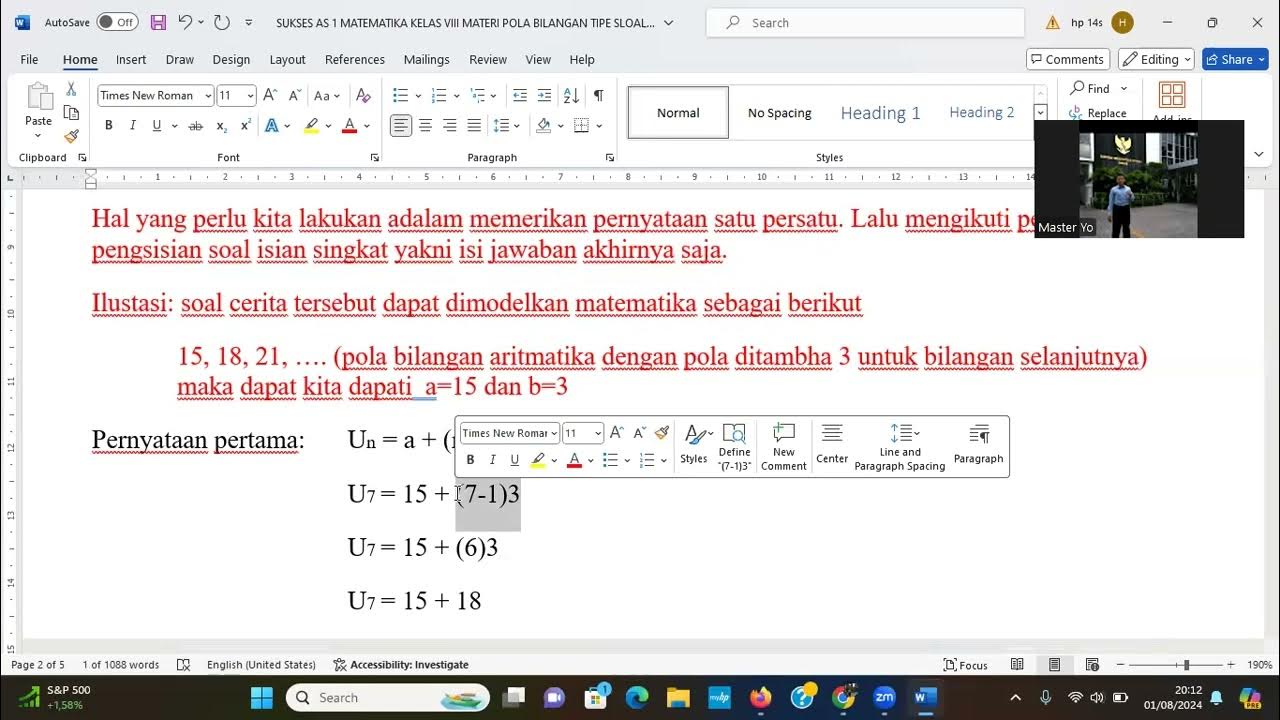
Latihan Soal Pola Bilangan

Baris dan Deret Geometri | Matematika Kelas X Fase E Kurikulum Merdeka

Pembahasan BARISAN DAN DERET (Aritmetika & Geometri) KELAS 11 | #MatematikAsik

Prediksi Soal Asesmen Sumatif Akhir Tahun Matematika Kelas 8 Tahun 2025 (Part 1)

pola bilangan kelas 8 part 1 (mudah)
5.0 / 5 (0 votes)
