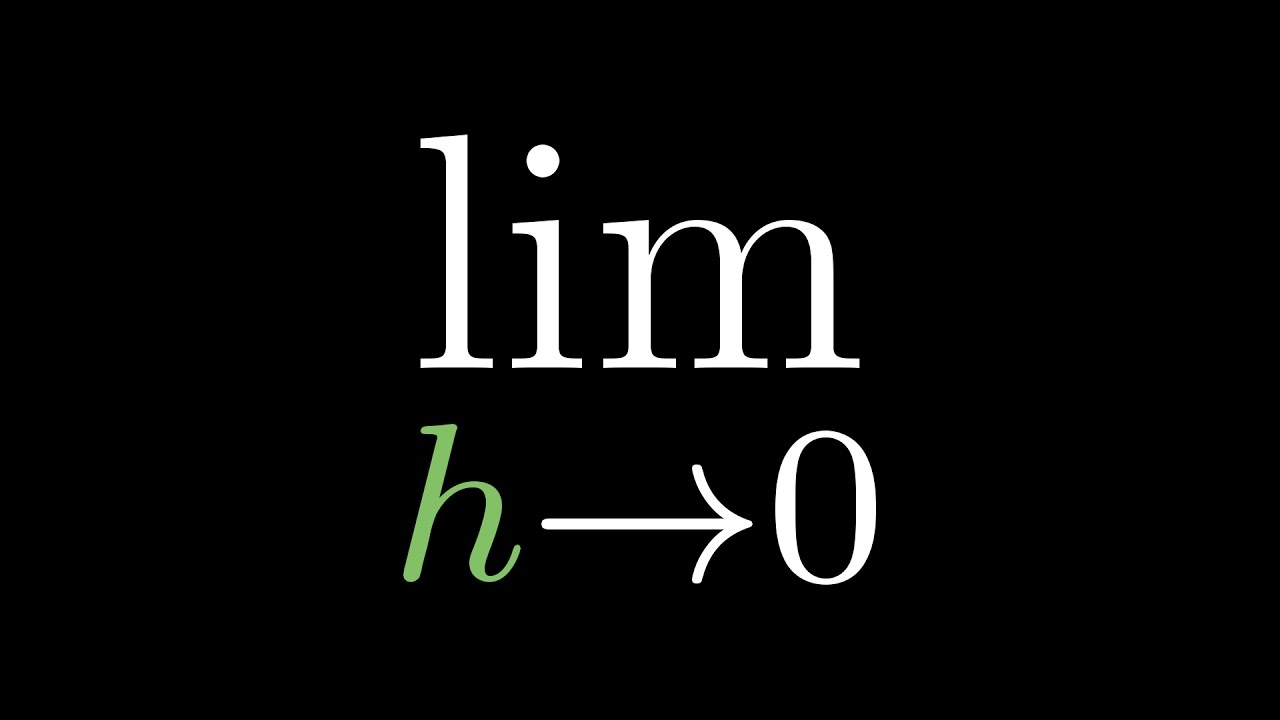Diferensiasi Numerik

Summary

In this lecture on numerical differentiation, the professor introduces the concept of derivatives in calculus, explaining how they are defined as limits. The lecture then explores three methods for numerical differentiation: forward, backward, and central difference. Using Taylor's series, the professor demonstrates how each method is derived and explains the formulas for first and second derivatives. The session concludes with tasks for students to prove the derived formulas and solve example problems related to the methods discussed. The lecture emphasizes understanding the mathematical foundations and their applications in computing derivatives.

Takeaways

• 😀 Introduction to numerical differentiation, focusing on derivative concepts.
• 😀 Derivative (or differential) is defined using limits in calculus: dY/dX = lim(ΔX -> 0).
• 😀 The derivative represents the slope of a function at a specific point, graphically visualized.
• 😀 The concept of numerical differentiation will involve using Taylor series expansions.
• 😀 Three primary numerical differentiation methods are introduced: Forward Difference, Backward Difference, and Central Difference.
• 😀 Forward Difference is derived from the Taylor series expansion and involves approximating the derivative using the value of the function at x+ΔX and x.
• 😀 Backward Difference is similar but uses the function values at x and x-ΔX for approximation.
• 😀 The second derivative can be approximated using forward differences, involving higher order terms from the Taylor expansion.
• 😀 The forward difference formula for the first derivative is derived and presented as a specific equation.
• 😀 Example problems are provided to apply the discussed methods and test understanding.
• 😀 The class concludes with encouragement to continue learning, with the next session promising more examples and discussions.

Q & A

What is the main topic of the lecture?

The main topic of the lecture is numerical differentiation, which is a method used to approximate derivatives of functions.

What is the definition of a derivative as described in the script?

The derivative is defined as the limit of the difference quotient as Delta X approaches zero. In mathematical terms, it's the limit of (f(x + Delta X) - f(x)) / Delta X as Delta X approaches zero.

How is the derivative visually represented on a graph?

On a graph, the derivative is represented as the slope of the tangent line to the curve at a given point. As Delta X approaches zero, the slope of the line becomes the derivative of the function.

What are the three formulas for numerical differentiation mentioned in the lecture?

The three formulas for numerical differentiation discussed are: 1) Forward difference, 2) Backward difference, and 3) Central difference.

How is the forward difference formula derived?

The forward difference formula is derived using the Taylor series expansion, where the derivative of a function at point x is approximated by (f(x + Delta X) - f(x)) / Delta X, with an error term included.

What is the backward difference formula?

The backward difference formula is another method for approximating derivatives, defined as (f(x) - f(x - Delta X)) / Delta X, with a corresponding error term.

How is the central difference formula different from the forward and backward formulas?

The central difference formula approximates the derivative using the average of the forward and backward differences, which provides a more accurate result than using either forward or backward difference alone.

How does the error in the numerical differentiation formulas behave?

The error in these formulas depends on Delta X. For the forward and backward differences, the error is proportional to Delta X. In the central difference formula, the error is proportional to the square of Delta X, making it more accurate for small values of Delta X.

What is the significance of the Taylor series in numerical differentiation?

The Taylor series is used to derive the formulas for numerical differentiation by expanding the function around a point, allowing us to approximate the derivative using the values of the function at nearby points.

What are the key takeaways from this lecture on numerical differentiation?

The key takeaways include understanding the definitions and formulas for numerical differentiation, the importance of the Taylor series in deriving these formulas, and the differences between the forward, backward, and central difference methods for approximating derivatives.