📌Cómo calcular el tamaño de la muestra. Población infinita o desconocida. Ejercicio Práctico
Summary
TLDREste video enseña cómo calcular el tamaño de una muestra para estimar la media de una población desconocida o infinita. Se destaca la importancia de una muestra adecuada y se presenta una fórmula que considera el nivel de confianza, el desvío estándar y el error máximo admitido. Se ofrece un ejemplo práctico para estimar los gastos semanales de gaseosa de un grupo familiar, utilizando el nivel de confianza del 95% y un rango de 100 a 700. El video también recomienda recursos para profundizar en estadística y proporciona un enlace para descargar la plantilla y bibliografía.
Takeaways
- 📚 El objetivo de una investigación es conocer una población, pero a menudo es imposible observar o encuestar a todas las unidades por cuestiones de tiempo y dinero.
- 🔍 Se debe tomar una muestra representativa de la población para realizar inferencias sobre ella, y esta muestra debe ser tomada al azar y tener un tamaño adecuado.
- 📉 La fórmula para calcular el tamaño de la muestra depende de tres factores: nivel de confianza (zeta), desvío estándar (s) y error muestral máximo admitido (E).
- 🔢 El desvío estándar (s) puede ser obtenido de estudios previos, a través de un estudio piloto o utilizando la regla del pulgar, que asume que el desvío es la sexta parte del rango de la variable.
- 📉 El nivel de confianza (zeta) se determina por el investigador y afecta el valor de Z, que para un 95% de confianza es aproximadamente 1.96.
- 📊 El error muestral máximo admitido (E) es elegido por el investigador y depende del tipo de investigación y los riesgos de la decisión que se tome.
- 📝 En el ejemplo práctico, se muestra cómo calcular el tamaño de la muestra para estimar los gastos semanales de gaseosa de un grupo familiar, utilizando un nivel de confianza del 95% y un rango de 100 a 700.
- 🧮 Se usa una fórmula específica para calcular el tamaño de la muestra, que es n = (Z * s) / E^2, donde Z es el valor de zeta, s es el desvío estándar y E es el error máximo admitido.
- 📚 Se recomienda el libro 'Investigación de mercados' de Zygmunt para profundizar en los conceptos de estadística y tamaño de muestra.
- 🔗 Se ofrece un enlace para descargar la plantilla y la información bibliográfica para aquellos interesados en ampliar su conocimiento sobre el tema.
Q & A
¿Cuál es el objetivo principal de tomar una muestra en una investigación estadística?
-El objetivo principal de tomar una muestra es conocer una población o un universo en estudio, lo cual a menudo es imposible debido al tamaño de la población, por lo que se utiliza una muestra para representar a toda la población.
¿Por qué es importante que la muestra sea tomada al azar?
-Es importante que la muestra sea tomada al azar para garantizar que sea una muestra probabilística, lo que permite una representación fidedigna de la población y permite la inferencia de los valores muestrales a la población.
¿Cuáles son los tres factores que se deben considerar para calcular el tamaño de la muestra?
-Los tres factores son el nivel de confianza dado por la zeta (z), el desvío estándar (s) y el error muestral máximo admitido elevado al cuadrado.
¿Cómo se puede determinar el desvío estándar (s) si no hay estudios previos?
-Si no hay estudios previos, se puede realizar un pequeño estudio piloto con una muestra más pequeña o usar la regla del pulgar, que asume que el desvío será la sexta parte del rango de la variable.
¿Qué nivel de confianza se utiliza en el ejemplo práctico del script?
-En el ejemplo práctico, se utiliza un nivel de confianza del 95%.
¿Cómo se calcula el valor de z para un nivel de confianza del 95%?
-Para un nivel de confianza del 95%, se calcula z como fz = 1 - alfa sobre 2, donde alfa es 0.05, y fz es 0.975, obteniendo z = 1.96.
¿Cuál es el error muestral máximo admitido en el ejemplo práctico del script?
-En el ejemplo práctico, el error muestral máximo admitido es de 20 pesos.
¿Cómo se utiliza la fórmula para calcular el tamaño de la muestra en el ejemplo práctico?
-Se utiliza la fórmula n = (z * s) / (error muestral máximo admitido)^2, donde z es 1.96, s es 100 y el error muestral es 20, resultando en un tamaño de muestra de 97.
¿Qué libro se recomienda para profundizar en el estudio de la investigación de mercados?
-Se recomienda el libro 'Investigación de Mercados' de Zygmunt, novena edición, específicamente en el capítulo 17.
¿Dónde se puede descargar la plantilla y la información bibliográfica mencionada en el script?
-Se puede descargar la plantilla y la información bibliográfica visitando el sitio web aprendizajeactivo.com o haciendo clic en la tarjeta proporcionada en el video.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Tamaño de Muestra para Variables Cuantitativas con Población Indefinida

Como Calcular el tamaño de la Muestra.wmv

Tamaño de Muestra para Variables Cuantitativas con Población Finita

Calculo del Tamaño de la Muestra para Poblaciones finitas e Infinitas
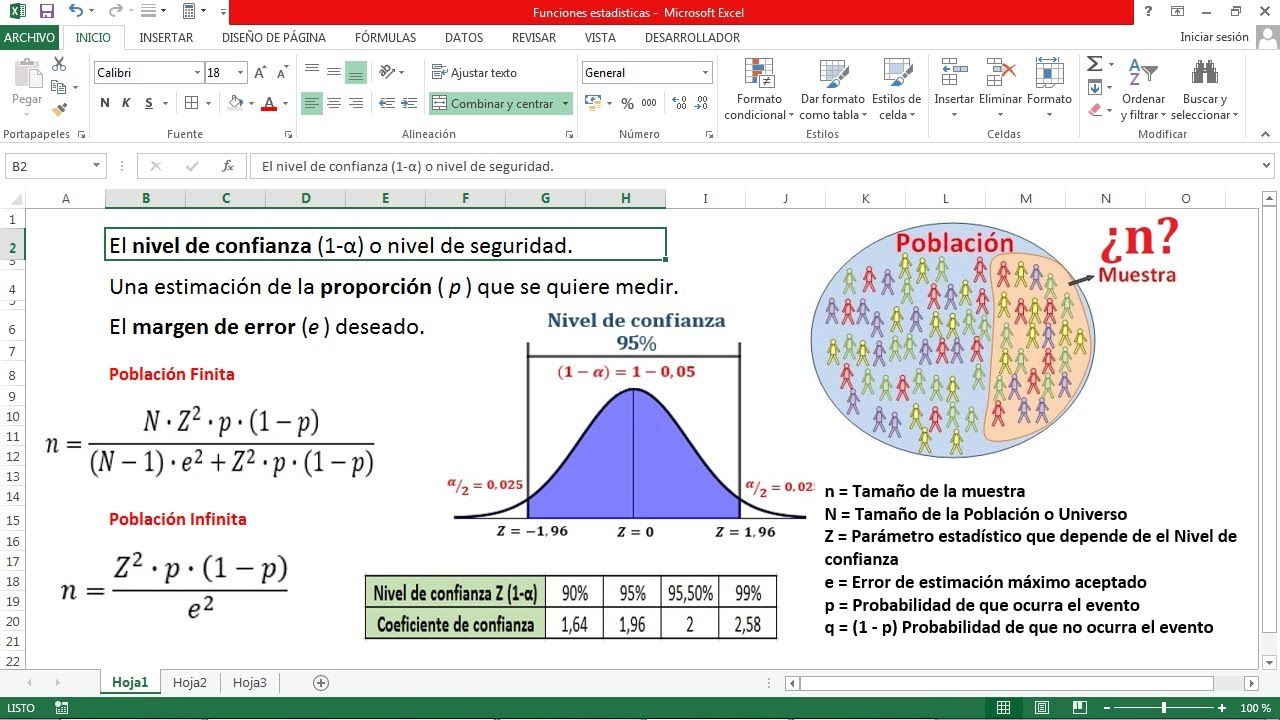
Cómo Calcular el Tamaño de la Muestra para Población Finita y Población Infinita con Excel.

How to determine the Sample Size?
5.0 / 5 (0 votes)