Properties of Functions
Summary
TLDRThis video introduces the properties of functions, focusing on key concepts like domain, range, maximum and minimum values, initial value, and zeros. It explains the notation of f(x), illustrating that it's just another way to represent y. The video also covers how to identify positive and negative intervals, as well as increasing, decreasing, and constant portions of a function. Special attention is given to the proper use of interval notation, open and closed circles, and how they affect the domain and range. Overall, it provides a foundational understanding of functions and their graphical representations.
Takeaways
- 😀 A function represents a relationship between two variables, where the output (Y) depends on the input (X).
- 😀 Linear functions, like y = ax + b, represent straight lines where the rate of change between X and Y is constant.
- 😀 'f(x)' is a notation used for a function of X, which is equivalent to writing Y, indicating Y depends on X.
- 😀 The domain of a function refers to the possible X values, and the range refers to the possible Y values that the function can take.
- 😀 The domain is written in interval notation, where square brackets mean inclusion and parentheses mean exclusion of values.
- 😀 The range is the set of all possible Y values, and it can extend to infinity (e.g., if the function continues upwards without bound).
- 😀 Extrema of a function are the maximum and minimum Y values, which represent the highest and lowest points on the graph.
- 😀 The initial value of a function is the point where it crosses the Y-axis, also known as the Y-intercept.
- 😀 Zeros of a function are the X values where the function crosses the X-axis, also called X-intercepts, and can occur multiple times.
- 😀 Positive values of a function are those above the X-axis, while negative values are those below the X-axis. These are expressed in intervals.
- 😀 A function can have increasing, decreasing, or constant intervals, which describe where the function rises, falls, or remains flat.
Q & A
What does the term 'function' refer to in mathematics?
-In mathematics, a function represents the relationship between two variables, where the value of one variable (Y) depends on the value of the other (X).
What is a linear function and how is it represented?
-A linear function is a type of function where the relationship between X and Y is represented by a straight line, typically in the form Y = ax + b, where 'a' is the slope and 'b' is the y-intercept.
What is the difference between a dependent and an independent variable in a function?
-In a function, the independent variable is typically X, which can be freely chosen, while the dependent variable is Y, whose value depends on the value of X.
What does the notation 'f(x)' mean in a function?
-The notation 'f(x)' is read as 'f of X' and it simply represents the value of the function for a specific X. It is another way of writing Y, indicating that Y depends on the value of X.
What are the main properties of functions discussed in this video?
-The main properties of functions discussed include domain, range, maximum and minimum values (extrema), initial value, zeros, positive and negative values, and intervals where the function is increasing, decreasing, or constant.
How do we determine the domain of a function?
-The domain of a function consists of all the possible X values that the function can take. In interval notation, we use brackets to include or exclude specific values based on the graph (full circle means inclusion, open circle means exclusion).
How is the range of a function different from the domain?
-The range of a function refers to all the possible Y values that the function can produce, while the domain refers to all the possible X values. The range is determined based on the function's graph and its vertical span.
What are extrema in the context of a function?
-Extrema are the maximum and minimum values of a function. The minimum value represents the lowest Y value the function reaches, while the maximum value represents the highest Y value it reaches.
What is the initial value of a function and where can it be found?
-The initial value of a function is the value of Y when X is equal to 0. This point is called the y-intercept and can be found by identifying where the function crosses the Y-axis.
What are zeros of a function, and how are they represented?
-Zeros of a function are the points where the function crosses the X-axis, meaning the Y value at these points is zero. These are also referred to as the x-intercepts of the function.
How do we identify the positive and negative values of a function?
-Positive values of a function are the sections where the function is above the X-axis, while negative values are the sections where the function is below the X-axis. These are expressed in intervals using proper interval notation.
What does it mean for a function to be increasing, decreasing, or constant?
-A function is increasing when its slope is positive, meaning the Y values go up as X increases. It is decreasing when the slope is negative, meaning Y decreases as X increases. A constant function has a slope of zero, and its Y value does not change as X changes.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

2.21 The Extreme Value Theorem

رياضيات 3 - ثالث ثانوي - درس : تحليل التمثيلات البيانية للدوال والعلاقات

Functions and Graphs | Precalculus

Lec - 25 B - Examples of Quadratic Functions
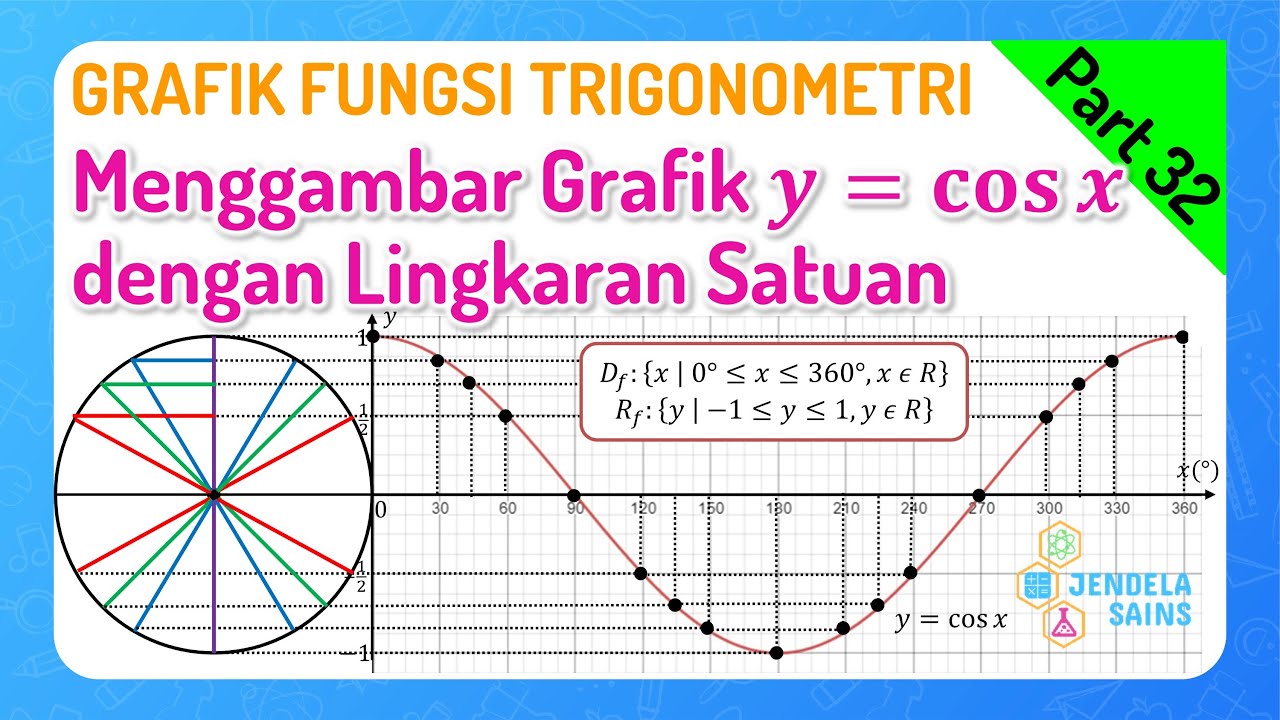
Trigonometri Matematika Kelas 10 • Part 32: Menggambar Grafik Fungsi y=cos x dengan Lingkaran Satuan

AP Precalculus – 1.1 Change in Tandem
5.0 / 5 (0 votes)
