Net Torque on a Door Problem
Summary
TLDRIn this educational video, the hosts discuss calculating the net torque on a door when three people push on it from different positions. They explore the torque formula and apply it to the forces exerted by Kate, Geneve, and Ryan. After calculating individual torques, the importance of the right-hand rule is emphasized to determine the direction of the net torque. The final result shows that the net torque is 40 newton meters, causing the door to rotate counterclockwise. The hosts encourage viewers to consider both the magnitude and direction of torque in physics problems.
Takeaways
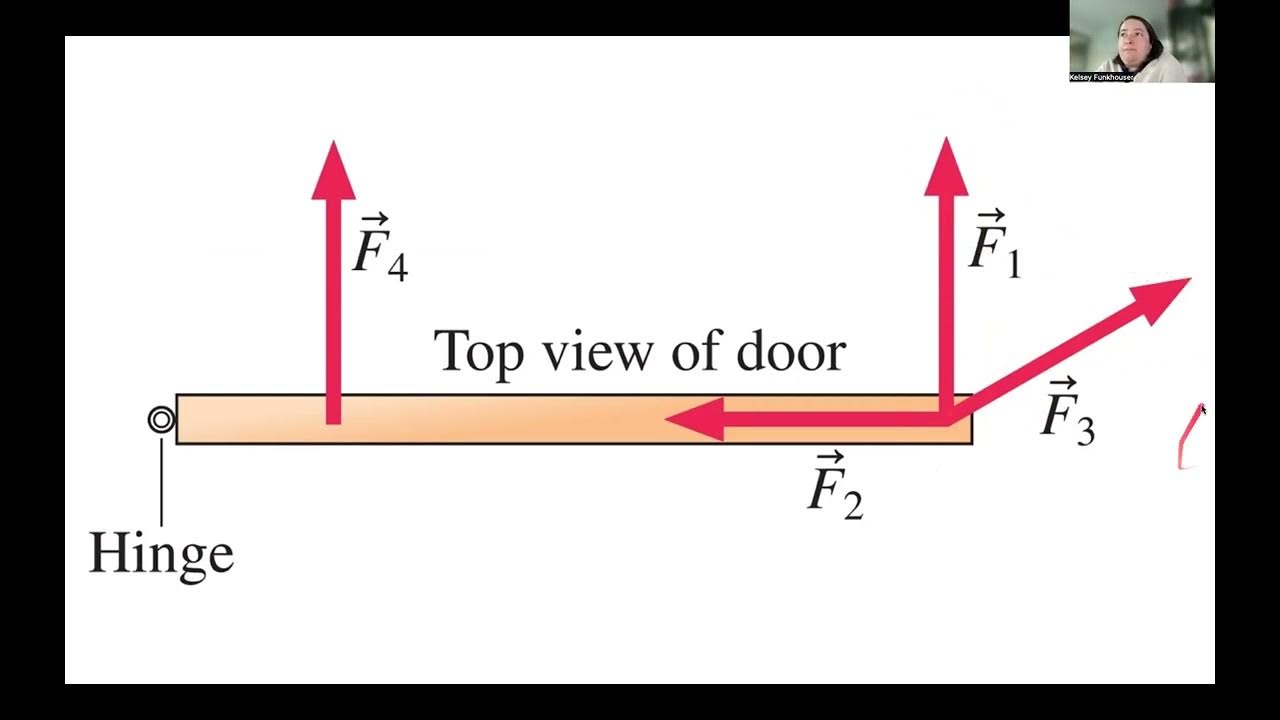
- 😀 The problem involves determining the net torque on a door pushed by three people (Kate, Geneve, and Ryan).
- 😀 Torque is calculated using the formula: Torque = r * F * sin(θ), where 'r' is the distance from the axis of rotation, 'F' is the force applied, and 'θ' is the angle between the force vector and the r vector.
- 😀 Kate's torque is zero because her point of application is at the hinge, meaning her distance from the axis of rotation is zero.
- 😀 Ryan's torque is calculated using a force of 160 N, a distance of 0.74 meters, and an angle of 55 degrees, resulting in 96.99 N·m.
- 😀 Geneve's torque uses a force of 170 N, a distance of 0.37 meters, and an angle of 115 degrees, resulting in 57.01 N·m.
- 😀 Kate’s torque doesn't contribute to the net torque due to the zero value of 'r' at her point of application.
- 😀 The total net torque is the sum of Ryan’s and Geneve’s torques, calculated as 153.99 N·m (rounded to 150 N·m for significant figures).
- 😀 The right-hand rule is essential for determining the direction of torque (clockwise or counterclockwise).
- 😀 Ryan’s torque is positive because it causes a counterclockwise rotation, as determined by the right-hand rule.
- 😀 Geneve’s torque is negative because it causes a clockwise rotation from the observer's perspective, based on the right-hand rule.
- 😀 The correct net torque, accounting for direction, is 40 N·m (positive), indicating a counterclockwise rotation of the door.
Q & A
What is the key concept of the problem in the transcript?
-The key concept revolves around calculating the net torque caused by three forces applied to a door. Torque is calculated using the equation: torque = r × F × sin(θ), where r is the distance from the axis of rotation, F is the force applied, and θ is the angle between the r vector and the force vector.
What does torque depend on in this scenario?
-Torque depends on three factors: the distance from the axis of rotation (r), the magnitude of the applied force (F), and the angle (θ) between the force and the direction of the r vector.
What is the value of torque for Kate, and why?
-Kate’s torque is zero because her distance (r) from the axis of rotation is zero, making the product of r and the force (F) also zero, regardless of the force applied.
How are the angles for the different forces determined?
-The angle (θ) for each force is determined based on the direction of the force relative to the axis of rotation. For Ryan, the angle is 55 degrees, for Geneve, it is 115 degrees, and for Kate, the angle is undefined since her distance from the axis is zero.
What is the significance of the right-hand rule in this problem?
-The right-hand rule is used to determine the direction of the torque. By curling the fingers of the right hand in the direction of the force, the thumb indicates whether the torque is positive (counterclockwise) or negative (clockwise).
What did the group initially forget to apply in solving the problem?
-The group initially forgot to apply the right-hand rule, which is essential for determining the direction of the torques and calculating the net torque correctly.
What does a positive net torque indicate in this scenario?
-A positive net torque indicates that the door will angularly accelerate in a counterclockwise direction from the observer’s viewpoint.
How are the magnitudes of the torques calculated for Ryan and Geneve?
-Ryan's torque is calculated as 0.74 meters × 160 newtons × sin(55 degrees), resulting in 96.99 newton meters. Geneve's torque is calculated as 0.37 meters × 170 newtons × sin(115 degrees), resulting in 57.01 newton meters.
What does the final net torque calculation result in?
-The final net torque calculation results in 39.98 newton meters, or approximately 40 newton meters with two significant figures, indicating a counterclockwise angular acceleration of the door.
What would have been the net torque if Kate's force had been applied from a different distance?
-If Kate's force had been applied from a non-zero distance, it would have contributed a non-zero torque, depending on the force applied and the angle of the force. The net torque would then be a sum of all three forces, factoring in the direction of each torque.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Dinamika rotasi momen gaya (Fisika SMA/MA Sagufindo kls XI smt 1)
Drehmoment berechnen + Erklärung des Hebelgesetz - einfach erklärt mit Beispielen

Rotational Form of Newton's Second Law - Introduction

FISIKA KELAS XI || Momen Gaya dan Momen Inersia || DINAMIKA ROTASI DAN KESETIMBANGAN BENDA TEGAR
PHYS 121 - Week 6 Lecture 3 - Torque

Dot vs. cross product | Physics | Khan Academy
5.0 / 5 (0 votes)
