Grade 11 Sc | Ch 7: Kinematics | 7.3. Position Vector (1)
Summary
TLDRThis video explains the concept of position vectors in two-dimensional space, emphasizing how to determine the position of an object based on its x and y components. It discusses the calculation of position vectors, including the use of unit vectors and the Pythagorean theorem to find the magnitude of a vector. Through examples, it illustrates how to express the position of points, compute the magnitude, and understand the movement along the x and y axes. The video offers a detailed explanation of vector components and provides practical guidance for calculating distances in two-dimensional motion.
Takeaways
- 😀 A position vector defines the location of an article on a path, either in the 'x' or 'y' direction, with small letters like 'r' used to denote it.
- 😀 The 'r' vector is expressed in meters (SI units), and the displacement is calculated based on the movement along the axis.
- 😀 The position vector in the x-direction is calculated as the product of the distance 'x' and the unit vector 'i'. Positive values indicate movement to the right, and negative values indicate movement to the left.
- 😀 Similarly, in the y-direction, the position vector is calculated as the product of the distance 'y' and the unit vector 'j', with positive values for upward movement and negative for downward movement.
- 😀 In two-dimensional space, the position vector is a combination of both the x and y components, expressed as: r = x * i + y * j.
- 😀 To calculate the magnitude of the vector, the expression involves the Pythagorean theorem: magnitude = √(x² + y²).
- 😀 In previous years, the magnitude of vectors was calculated using only the x or y components individually, but now it includes both components together.
- 😀 The script uses an example of a moving football to illustrate how position vectors can be written for different points like A, B, C, and D along its path.
- 😀 For example, the position vector of point A is expressed as -1i + 0j, as it lies on the x-axis with no movement along the y-axis.
- 😀 The magnitude of the vector can be found by applying the formula √(x² + y²), and similar steps are used for other points like B, C, and D to compute the distance from the origin.
- 😀 The concepts discussed are reinforced through practical examples and visual aids, allowing for a clearer understanding of how position vectors work in two dimensions.
Q & A
What is a position vector as mentioned in the script?
-A position vector determines the location of an object along a path. It is defined by coordinates on the x and y axes and is used to represent the location of an article moving along a trajectory.
What does the letter 'r' signify in the context of position vectors?
-The letter 'r' represents the position vector in this context, which is the vector indicating the position of an object at a particular time.
How is the position vector represented on the x-axis?
-On the x-axis, the position vector 'r' is represented as 'r = x * i', where 'x' is the distance from the origin and 'i' is the unit vector. The sign of 'x' indicates direction: positive for movement to the right and negative for movement to the left.
How is the position vector represented on the y-axis?
-On the y-axis, the position vector 'r' is expressed as 'r = y * j', where 'y' is the distance from the origin and 'j' is the unit vector. The sign of 'y' indicates direction: positive for upward movement and negative for downward movement.
What is the expression for the position vector in two dimensions?
-In two dimensions, the position vector is expressed as 'r = x * i + y * j', where 'x' and 'y' are the distances on the x and y axes, and 'i' and 'j' are the unit vectors along those axes.
What is the formula to calculate the magnitude of the position vector?
-The magnitude of the position vector is calculated using the Pythagorean theorem: 'magnitude = √(x² + y²)', where 'x' and 'y' are the components of the position vector along the x and y axes.
What does the term 'magnitude' refer to in this context?
-The term 'magnitude' refers to the length of the position vector, which represents the distance from the origin to the object’s location.
How is the magnitude of the position vector for point D calculated?
-For point D, the magnitude is calculated as 'magnitude = √(5² + 3²) = √34', which gives the distance between the origin and point D.
What is the difference between the position vector and the unit vector?
-The position vector defines the location of an object, while the unit vector is a direction vector with a magnitude of 1. The position vector is scaled by the magnitude of the distance to the object, and the unit vector represents the direction of movement.
Can you explain how to write the position vector for points A, B, C, and D?
-To write the position vectors for points A, B, C, and D, we first determine the x and y components for each point. For example, for point A, the position vector is '-1 * i + 0 * j', for point B it is '0 * i + 1 * j', and for point C, it is '2.5 * i + 3 * j'. The position vectors are then written based on these components.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Gerak Dua Dimensi "Fisika Dasar"

Vektor Matematika Kelas 10 • Part 4: Vektor di Bidang Koordinat & Vektor Posisi
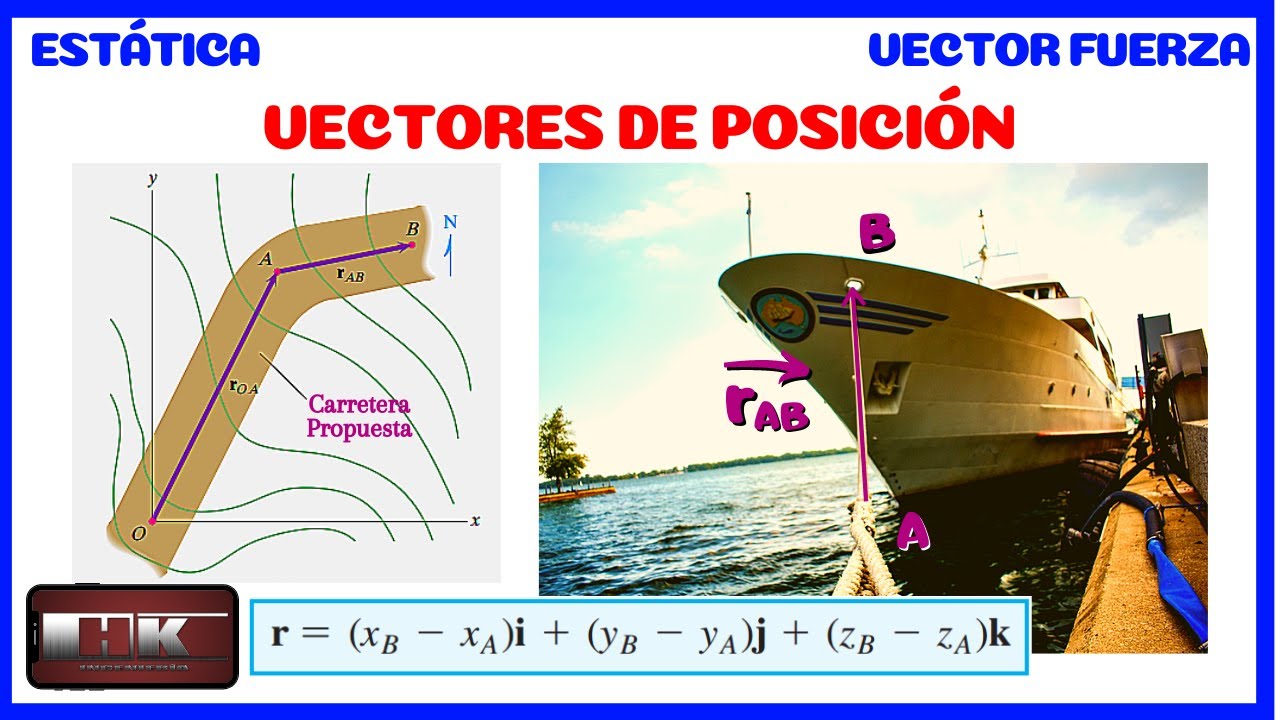
VECTORES DE POSICION. TEORÍA Y CONCEPTOS DE ESTÁTICA 👨🏫
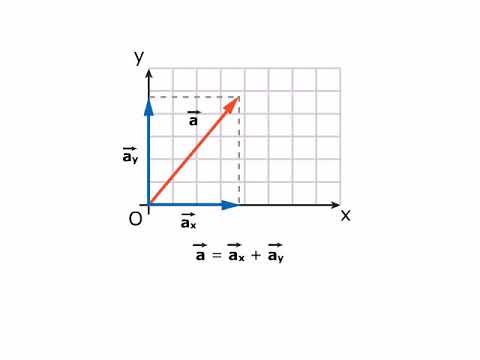
TEORIA Versori e componenti cartesiane di un vettore AMALDI ZANICHELLI

kompleks 02 bagian real dan imajiner

Statika Partikel 3D (1/5): Komponen Gaya dalam Tiga Dimensi
5.0 / 5 (0 votes)
