Asal Usul Akar 3 (√3) Pada Tegangan 3 Phasa
Summary
TLDRThis video explores the concept of the square root of 3 (√3) in the context of three-phase voltage systems. It delves into the origins of this mathematical factor and how it plays a critical role in the calculation of voltages, currents, and power distribution in three-phase electrical systems. Understanding √3 is essential for engineers and electricians working with three-phase power, as it influences the design and analysis of electrical circuits and systems.
Takeaways
- 😀 The concept of three-phase voltage is fundamental in electrical engineering, especially for power transmission.
- 😀 √3 (the square root of three) plays a key role in calculating the relationship between line voltage and phase voltage in three-phase systems.
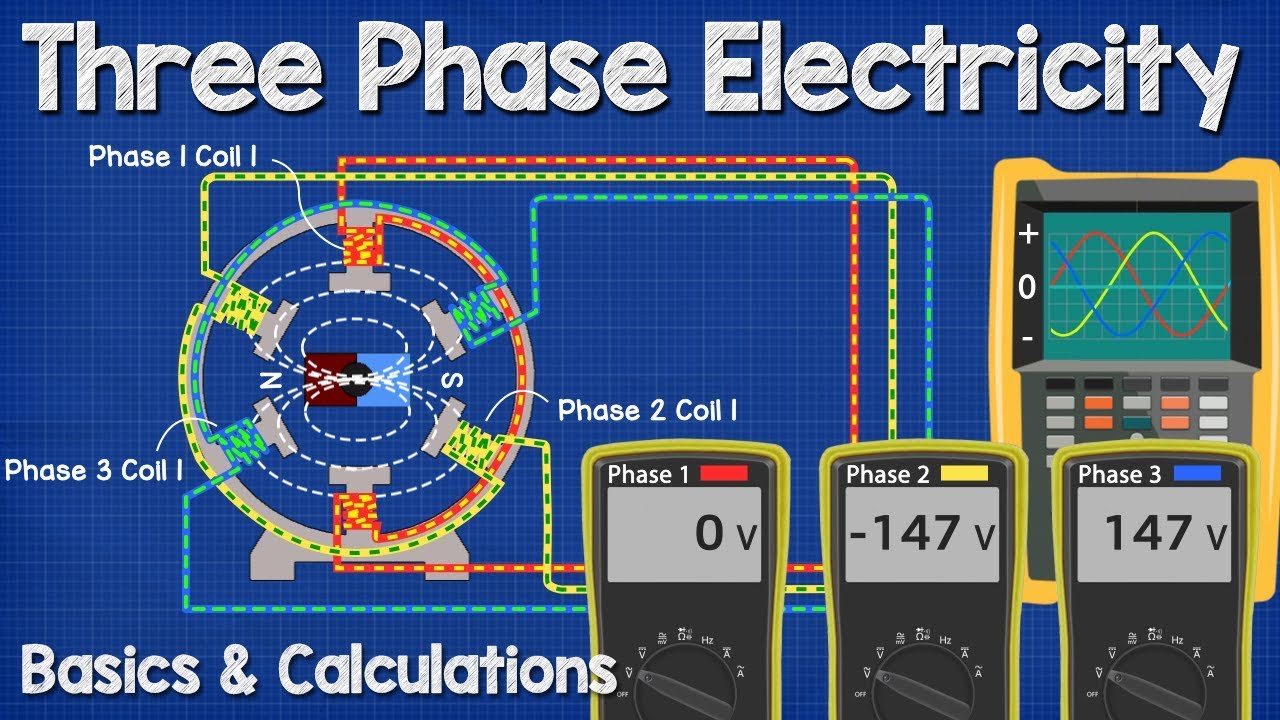
- 😀 The formula V_line = √3 * V_phase is essential to understanding how line-to-line and line-to-neutral voltages relate in a three-phase system.
- 😀 The √3 factor emerges due to the geometry of the three-phase system, specifically from the 120-degree phase difference between the phases.
- 😀 The use of √3 helps ensure the power delivery remains balanced across the system, optimizing efficiency in electrical networks.
- 😀 In practical applications, √3 is used to calculate current and power in both balanced and unbalanced three-phase systems.
- 😀 The derivation of √3 from trigonometric principles and the geometry of rotating vectors is a key aspect in electrical engineering.
- 😀 Understanding √3 is crucial for designing and maintaining three-phase electrical systems, including motors, generators, and transformers.
- 😀 The origin of √3 highlights the importance of phase relationships in multi-phase systems, influencing voltage drop and power distribution.
- 😀 Electrical engineers use the √3 factor to optimize electrical installations and reduce losses in three-phase power systems.
Q & A
What is the significance of √3 in a three-phase voltage system?
-In a three-phase voltage system, √3 is important because it represents the relationship between the line voltage (the voltage measured between two phases) and the phase voltage (the voltage measured from any one phase to neutral). This factor helps in converting phase voltage to line voltage and vice versa.
Why is √3 specifically used in three-phase power calculations?
-√3 (approximately 1.732) is used because of the geometry of the three-phase system. The voltage between phases forms a 120-degree separation, which leads to the √3 factor when calculating the relationship between line and phase voltages.
How is the line voltage in a three-phase system calculated from the phase voltage?
-To calculate the line voltage (V_line) from the phase voltage (V_phase), the formula is V_line = V_phase × √3. This is based on the vector relationships between the phase voltages.
What is the relationship between phase current and line current in a three-phase system?
-In a balanced three-phase system, the phase current (I_phase) is equal to the line current (I_line), meaning I_line = I_phase. However, the voltage relationship between phase and line voltage is where the √3 factor comes into play.
Can the origin of √3 be understood from a geometrical perspective?
-Yes, the origin of √3 can be traced back to the geometry of the three-phase system. The 120-degree phase difference between each of the three voltages forms an equilateral triangle when represented as phasors, and √3 emerges as a result of this geometric configuration.
What happens if the phase voltages in a three-phase system are not balanced?
-If the phase voltages are unbalanced, it can cause irregularities in power delivery, leading to inefficiencies, overheating of equipment, and potential damage. The relationship involving √3 assumes balanced conditions, so unbalanced voltages will disrupt the expected calculations.
In which situations is it necessary to apply the √3 factor in electrical systems?
-The √3 factor is essential when calculating the total power, line-to-line voltage, or any voltage-related measurements in three-phase electrical systems. It is especially relevant in industrial and large-scale electrical installations that use three-phase power.
How do you convert line-to-line voltage to phase voltage in a three-phase system?
-To convert line-to-line voltage to phase voltage, divide the line voltage by √3. The formula is V_phase = V_line / √3.
What is the role of the √3 factor in power factor correction?
-The √3 factor is not directly related to power factor correction, but it plays a role in calculating the total power in a three-phase system, which is necessary for determining how much correction is required. Power factor correction aims to improve efficiency by reducing reactive power.
Why is three-phase power more efficient than single-phase power?
-Three-phase power is more efficient than single-phase power because it provides a continuous power flow. In a three-phase system, the power is delivered in a more stable manner with less fluctuation, reducing the need for larger and more expensive wiring and equipment compared to single-phase systems.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahora5.0 / 5 (0 votes)