TIRO VERTICAL hacia arriba 🚀 (MRUV/MRUA) Cómo calcular la Altura y el Tiempo
Summary
TLDREste video explica cómo resolver problemas de movimiento vertical utilizando las ecuaciones del tiro vertical, enfocándose en dos casos específicos. En el primero, se calcula la altura alcanzada por una piedra cuando su velocidad se reduce a la mitad, usando la ecuación adecuada para el movimiento uniformemente acelerado. En el segundo, se aborda un problema con un balón lanzado, determinando el tiempo que tarda en alcanzar la altura máxima y la altura alcanzada. A lo largo del video, se detallan los pasos y las fórmulas utilizadas, ofreciendo un enfoque claro y detallado para entender cómo resolver estos ejercicios de física.
Please replace the link and try again.
Q & A
¿Cuál es la velocidad inicial de la piedra lanzada en el primer ejercicio?
-La velocidad inicial de la piedra es de 16 metros por segundo.
¿Qué se pide calcular en el primer ejercicio?
-Se pide calcular la altura máxima que alcanza la piedra cuando su velocidad se reduce a la mitad, es decir, a 8 metros por segundo.
¿Qué valor se toma para la aceleración debida a la gravedad en el primer ejercicio?
-La aceleración debida a la gravedad se toma como 9.8 metros por segundo al cuadrado y es negativa debido a que la gravedad actúa como desaceleración en un movimiento vertical hacia arriba.
¿Qué fórmula se usa para calcular la altura máxima de la piedra?
-La fórmula utilizada para calcular la altura es: h = (v_f^2 - v_i^2) / (2 * g), donde v_f es la velocidad final, v_i es la velocidad inicial y g es la aceleración debida a la gravedad.
¿Cuál es la altura máxima que alcanza la piedra en el primer ejercicio?
-La altura máxima que alcanza la piedra es aproximadamente 9.8 metros.
¿Qué se pide calcular en el segundo ejercicio con el balón?
-En el segundo ejercicio, se pide calcular el tiempo que tarda el balón en alcanzar la altura máxima y la altura máxima que alcanza el balón.
¿Qué valor se toma para la aceleración debida a la gravedad en el segundo ejercicio?
-En el segundo ejercicio, la aceleración debida a la gravedad se toma como -9.8 metros por segundo al cuadrado, siendo negativa porque la gravedad actúa en dirección opuesta al movimiento del balón.
¿Cómo se calcula el tiempo que tarda el balón en alcanzar la altura máxima?
-El tiempo se calcula utilizando la fórmula: t = (v_f - v_i) / g, donde v_f es la velocidad final (0 m/s en la altura máxima), v_i es la velocidad inicial y g es la gravedad. En este caso, el tiempo es aproximadamente 1.0 segundo.
¿Cuál es la altura máxima que alcanza el balón en el segundo ejercicio?
-La altura máxima que alcanza el balón es aproximadamente 5.1 metros.
¿Por qué se utiliza el valor 1.0 en lugar de solo 1 al escribir el tiempo?
-El valor 1.0 se utiliza para indicar que se ha hecho una aproximación a un decimal, mostrando que el tiempo se ha redondeado a 1.0 segundos, aunque numéricamente también puede expresarse como 1.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Caída libre #2. MRUA MRUV. Lanzamiento vertical. Todosobresaliente.com

Tiro Parabólico Horizontal | Explicación completa | cómo deducir las fórmulas

Cómo analizar cualquier ejercicio de Tiro parabólico de forma fácil y rápida.

Física Grado Noveno Semana 18 y 19: Movimiento Parabólico
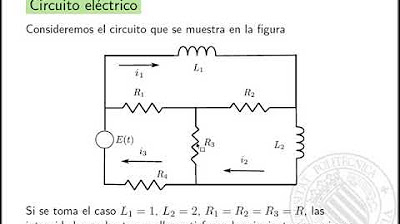
Ecuaciones diferenciales con Mathematica: Apliaciones de los sistemas de ecuaciones diferen | | UPV

MRU Problema de ENCUENTRO 🚌➡⬅🚙
5.0 / 5 (0 votes)