Mengenal Bangun Ruang Kerucut
Summary
TLDRIn this educational video, viewers are introduced to the geometry of a cone, a 3D shape with a circular base and a slanted surface. The script explains the key elements of a cone, including its parts like the radius, height, diameter, slant height, and surface area. Real-life examples such as traffic cones, ice cream cones, and birthday hats are used to make the topic relatable. The video also discusses mathematical relationships, such as the Pythagorean theorem, applied to cones. Overall, the video provides a comprehensive yet accessible guide to understanding the geometry of cones.
Takeaways
- 😀 Cones are 3D shapes that are defined by two main components: a circular base and a slanted side, known as the 'selimut' (slant height).
- 😀 Real-life examples of cones include ice cream cones, traffic cones, 'nasi tumpeng' (traditional rice cone dish), birthday hats, and farmer's cap.
- 😀 A cone consists of two surfaces: the flat circular base and the curved surface (slant height), which is often referred to as the 'selimut'.
- 😀 The radius of a cone refers to the distance from the center of the base to its edge, commonly denoted as 'r'.
- 😀 The diameter of a cone is the full width of the base, calculated as twice the radius (denoted as 'D').
- 😀 The height of a cone is the vertical distance from the apex (top point) to the center of the base, denoted as 't'.
- 😀 The slant height of the cone is the distance from the apex to any point on the edge of the base, represented as 's'.
- 😀 The relationship between the radius, height, and slant height of a cone follows the Pythagorean theorem: s² = t² + r².
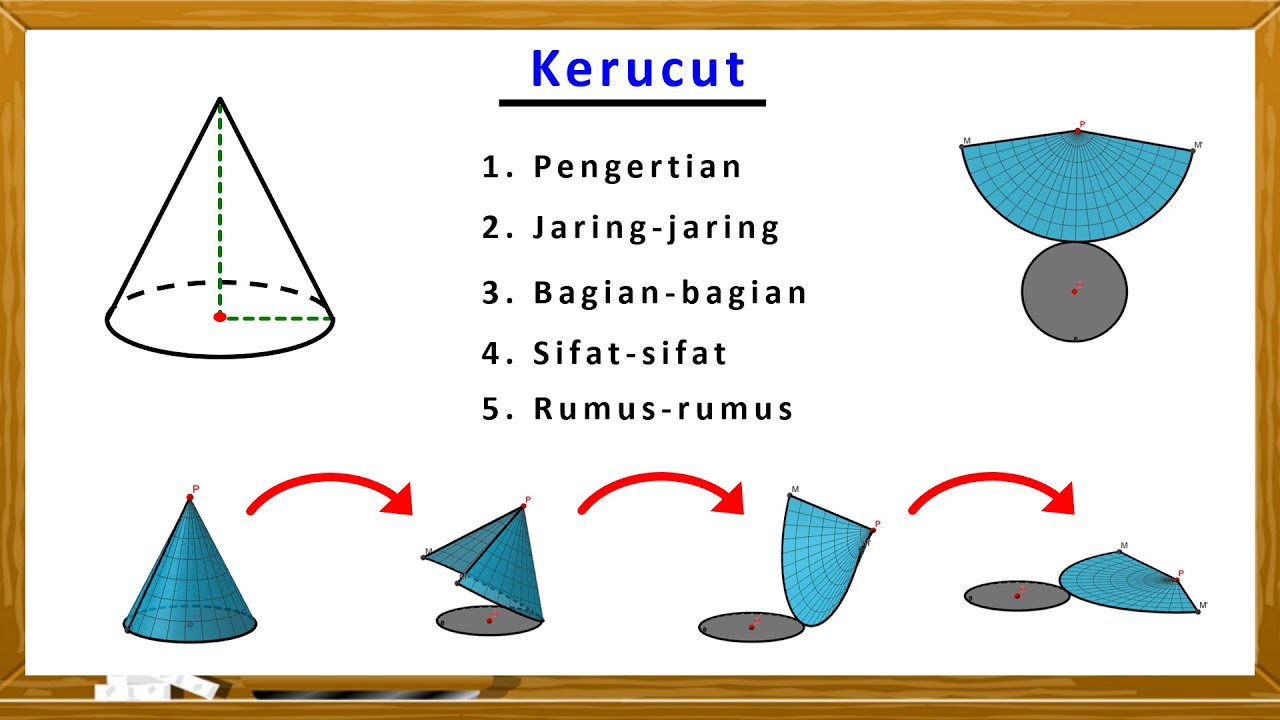
- 😀 A cone's net consists of two parts: the circular base and a sector (a portion of a circle) that forms the slanted side.
- 😀 The lesson encourages viewers to engage with the content by liking, commenting, subscribing, and sharing the video to spread knowledge.
Q & A
What is a cone in geometry?
-A cone is a three-dimensional geometric shape that has a circular base and a curved surface that meets at a single point called the apex. It is also referred to as a 'bangun ruang kerucut' in Indonesian.
Can you give examples of cones in everyday life?
-Yes, common examples of cones include ice cream cones, traffic cones, the traditional cone-shaped rice dish known as 'nasi tumpeng,' birthday hats, and a farmer's cap (caping).
What are the two main sides of a cone?
-The two main sides of a cone are the base, which is a circular flat surface, and the slant height or lateral surface, often referred to as the 'selimut' kerucut.
What is the radius of a cone?
-The radius of a cone refers to the distance from the center of the circular base to the edge. It is denoted as 'r' in the geometric representation.
What is the diameter of a cone?
-The diameter of a cone is the straight line that passes through the center of the base and touches both edges of the circle. It is twice the radius and is denoted by 'D'.
What is the height of a cone?
-The height of a cone is the vertical distance from the apex (the tip) of the cone to the center of the base. It is denoted as 't'. The height is perpendicular to the diameter of the base.
What is the slant height of a cone?
-The slant height of a cone, denoted by 's,' is the distance from the apex to any point on the circumference of the base. It is the slanted edge of the cone.
How is the relationship between the slant height, radius, and height of a cone represented mathematically?
-The relationship between the slant height (s), radius (r), and height (t) of a cone is described by the Pythagorean theorem: s² = t² + r².
What is the net of a cone?
-The net of a cone is a two-dimensional representation obtained by slicing the cone along its slant height and unrolling it. It consists of a circular base and a sector of a circle (the lateral surface) with a radius equal to the slant height.
What is the importance of understanding the elements of a cone?
-Understanding the elements of a cone, such as the base, radius, diameter, height, and slant height, is crucial for solving problems related to surface area, volume, and other geometric calculations. It helps visualize the cone's structure and its application in real-life scenarios.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Bangun Ruang Sisi Datar [Part 4] - Limas
KERUCUT. Pengertian, Jaring-jaring Kerucut, Bagian-bagian Kerucut, Sifat-sifat & Rumus-rumus Kerucut

3 LUAS PERMUKAAN KERUCUT - BANGUN RUANG SISI LENGKUNG - KELAS 9 SMP

COMO HACER UN CONO DE PAPEL FIGURA GEOMETRICA

Pembuktian Luas Permukaan dan Volume Bangun Ruang Sisi Lengkung

(Asal Usul) Pembuktian Rumus Luas Permukaan Kerucut - Bangun Ruang Sisi Lengkung - Matematika SMP
5.0 / 5 (0 votes)
