Varianza y Desviación Estándar - Ejercicio 2
Summary
TLDREn este video, Jorge explica cómo calcular la varianza y la desviación estándar para una muestra de datos. Usando un ejemplo de salarios por hora de trabajadores, muestra paso a paso cómo aplicar las fórmulas estadísticas para obtener la media muestral, luego calcular la varianza y finalmente derivar la desviación estándar. A lo largo de la explicación, Jorge destaca la importancia de la notación adecuada y la comprensión de las unidades en las fórmulas. El video es ideal para aquellos que buscan entender los conceptos fundamentales de la dispersión en estadísticas de manera clara y práctica.
Takeaways
- 😀 Se está resolviendo un problema de varianza y desviación estándar usando fórmulas para una muestra, no para una población.
- 😀 Los salarios por hora de una muestra de trabajadores son 12, 20, 16, 18 y 19 dólares, y se necesita calcular la varianza y la desviación estándar.
- 😀 Para la varianza muestral se usa la fórmula que involucra la resta de la media muestral de cada valor, al cuadrado, y luego se divide entre (n - 1).
- 😀 La media muestral se calcula sumando todos los valores y dividiendo entre el número de observaciones de la muestra (5 en este caso).
- 😀 El valor de la media muestral de este problema es 17 dólares.
- 😀 Para calcular la varianza muestral, se resta la media muestral de cada valor, se eleva al cuadrado y se suman los resultados. Luego, se divide entre (n - 1).
- 😀 La varianza muestral obtenida en este caso es 10 dólares cuadrados.
- 😀 La desviación estándar es la raíz cuadrada de la varianza. En este caso, es la raíz cuadrada de 10, lo que da aproximadamente 3.162 dólares.
- 😀 La desviación estándar tiene las mismas unidades que los datos originales (dólares), mientras que la varianza tiene unidades al cuadrado.
- 😀 Se incluye una tabla con símbolos para la media, varianza, desviación estándar y el número de elementos tanto para una población como para una muestra, destacando las diferencias entre estos conceptos.
- 😀 Es importante recordar la notación estándar usada en estadística, como sigma (σ) para la población y 's' para la muestra, ya que es común en libros de texto y exámenes.
Please replace the link and try again.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Rango, varianza, desviación estándar, coeficiente de variación, desviación media: datos no agrupados

Varianza y Desviación Estándar - Fórmulas Rápidas

Varianza y Desviación Estándar de Datos Agrupados de Variable Discreta
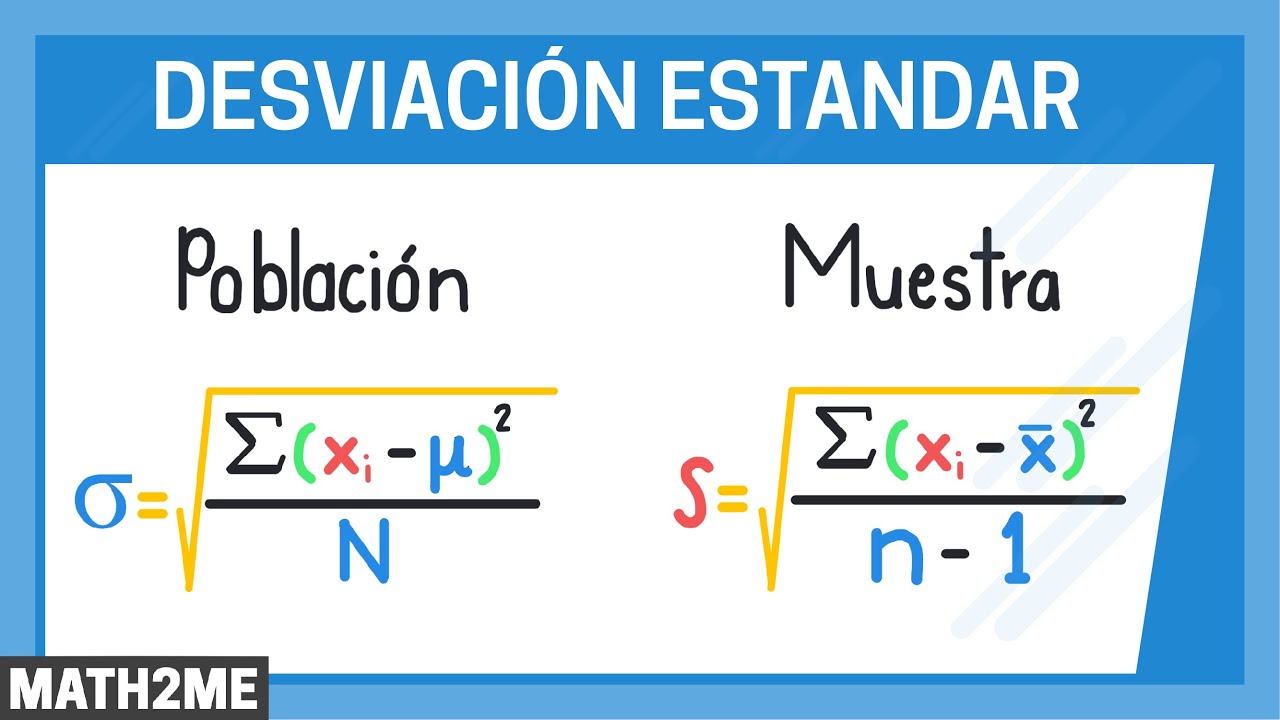
Desviación estándar en una población y muestra | Introdución | Fx-991EX

Varianza, Desviación Estandar y Coeficiente de Variación | Datos agrupados puntualmente

Media o valor esperado, varianza y desviación estándar de variable aleatoria discreta
5.0 / 5 (0 votes)