Integración numérica, Trapecio múltiple 02
Summary
TLDREn este video se explica cómo aplicar el método numérico de integración por el método trapezoidal, con ejemplos prácticos que varían el número de trapecios utilizados. Se analiza cómo ajustar la fórmula al aumentar la cantidad de trapecios (de 4 a 8, 10, etc.) y cómo se obtiene la suma para aproximar el área bajo una curva. Se introduce una relación entre el número de trapecios y la cantidad de evaluaciones de la función necesarias. Finalmente, se generaliza la fórmula para cualquier número de trapecios, permitiendo su uso con diferentes límites inferiores y superiores.
Takeaways
- 😀 El método trapezoidal es una técnica numérica utilizada para aproximar el área bajo una curva.
- 😀 En el ejemplo, se analizó cómo ajustar la fórmula para el caso de 4 trapecios, evaluando la función en puntos específicos.
- 😀 Se explicó cómo aumentar el número de trapecios (de 4 a 8) cambia la expresión de la aproximación del área.
- 😀 La fórmula se compone de la función evaluada en los límites inferior y superior, y en los puntos intermedios, donde la función se evalúa dos veces.
- 😀 La distancia entre los puntos de evaluación se calcula dividiendo la diferencia entre el límite superior y el límite inferior por el número de trapecios.
- 😀 A medida que el número de trapecios aumenta, el número de veces que la función se evalúa en los puntos intermedios también cambia.
- 😀 La relación entre el número de trapecios y las evaluaciones de la función muestra que si el número de trapecios es N, se evalúa la función en N-1 puntos intermedios.
- 😀 Un patrón en la fórmula es que la función se evalúa en los límites una vez, y en los puntos intermedios de forma múltiple (2 veces, 3 veces, etc.).
- 😀 Al generalizar la fórmula para cualquier número de trapecios, la suma de las evaluaciones de la función en los puntos intermedios se representa mediante una sumatoria.
- 😀 En la expresión final, se incluyen los límites de integración como variables, lo que permite adaptar la fórmula a cualquier intervalo de integración, no solo a [2, 10].
Please replace the link and try again.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Método del trapecio | Integración numérica |Métodos Numéricos | Parte 1 | ¡Muy básico!

Integración por partes ejemplo 2 | Cálculo integral - Vitual

MULTIPLICACIÓN CON DECIMALES POR LA UNIDAD SEGUIDA DE CEROS - por 10, 100 y 1000
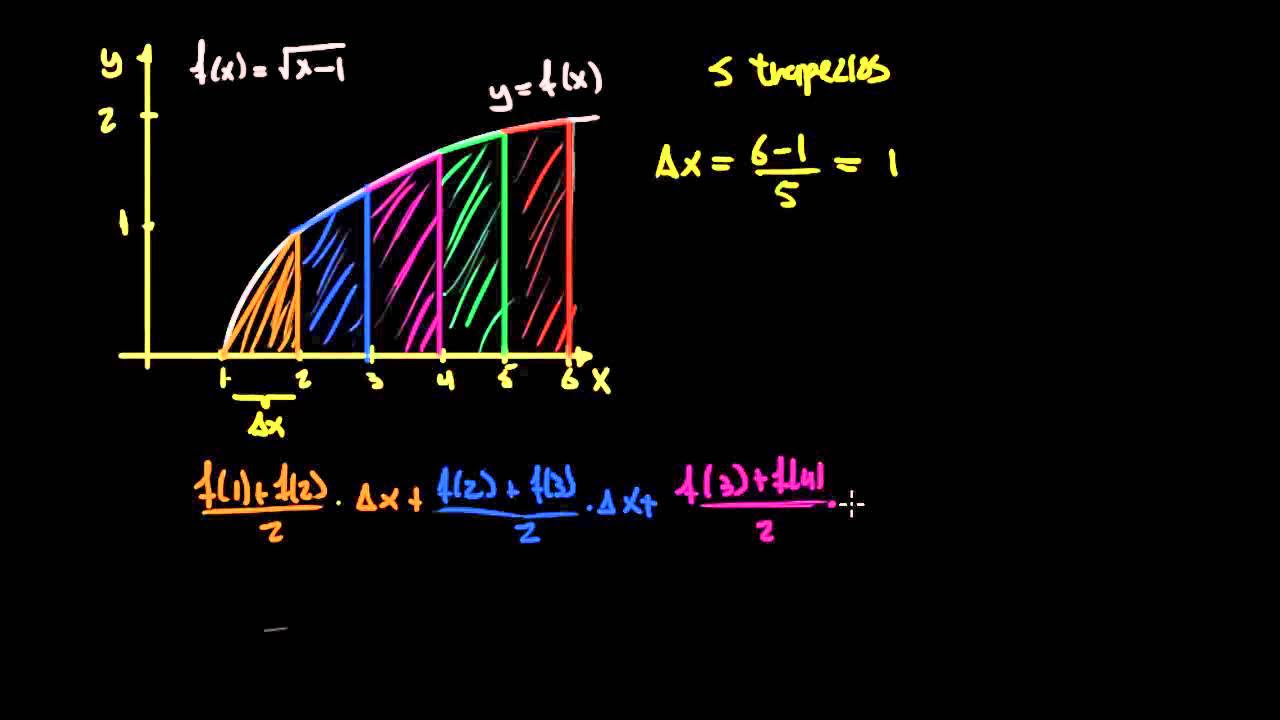
Aproximaciones trapzoidales del area bajo la curva

MÉTODO STAR: Destaca tus habilidades en tu próxima entrevista de trabajo

División de números decimales

¿Cómo hacer el PROBLEMA para tu Investigación de Éxito?🌟 |Dra.Rocio Lima 😇❤️🔥
5.0 / 5 (0 votes)