013 Correlación y Regresión Multiple Basico
Summary
TLDREn esta clase, se aborda la regresión múltiple, expandiendo el análisis de la relación entre una variable dependiente, la resistencia, y varias variables independientes: fuerza, potencia, temperatura y tiempo. Se discute la importancia del R cuadrado ajustado y se realizan pruebas de hipótesis para validar la relación entre las variables. Se concluye que solo la potencia y la temperatura son significativas para predecir la resistencia, y se elabora una ecuación de regresión que permite hacer pronósticos específicos, destacando la utilidad de la regresión múltiple en el análisis estadístico.
Takeaways
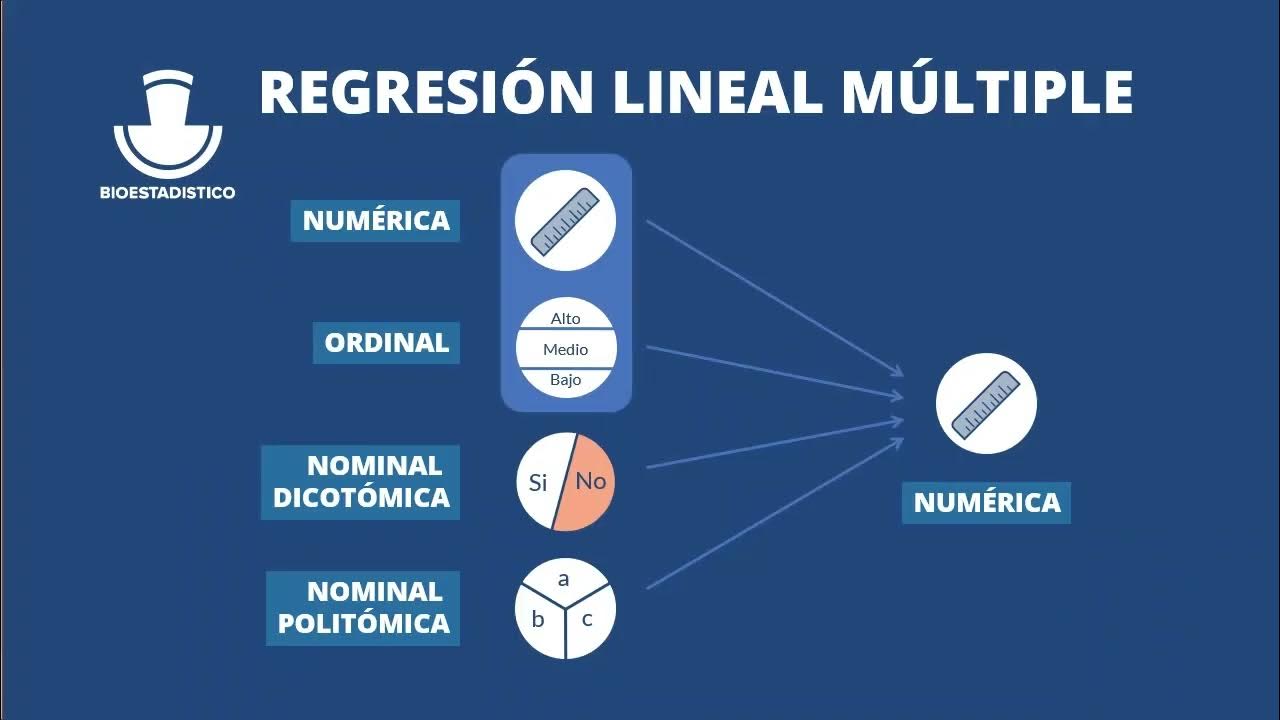
- 😀 La regresión múltiple permite analizar la relación entre una variable dependiente y múltiples variables independientes.
- 😀 La resistencia del pegamento es la variable dependiente, mientras que la fuerza, potencia, temperatura y tiempo son las variables independientes.
- 😀 El coeficiente de determinación ajustado (R² ajustado) indica que el modelo puede explicar el 66.8% de la variabilidad en la resistencia.
- 😀 Se realiza una prueba de hipótesis para evaluar la existencia de correlación múltiple entre la resistencia y las variables independientes.
- 😀 Un valor p muy bajo (0.0000) en la prueba ANOVA sugiere que hay una relación significativa entre las variables.
- 😀 Los coeficientes de regresión indican qué variables son relevantes para el modelo: solo potencia y temperatura resultan ser significativas.
- 😀 Beta 1 y Beta 4 se encuentran en cero, lo que significa que no contribuyen al modelo de regresión.
- 😀 La ecuación de regresión final se simplifica, considerando solo las variables de potencia (X2) y temperatura (X3).
- 😀 La ecuación de regresión se expresa como Y = -24.900 + 0.498X2 + 0.130X3 para predecir la resistencia.
- 😀 La identificación de variables relevantes es crucial en la regresión múltiple para construir modelos predictivos eficaces.
Q & A
¿Cuál es el objetivo principal de la clase sobre regresión múltiple?
-El objetivo principal es reconocer las características y cualidades de la regresión múltiple, validar modelos de relación múltiple e interpretar los resultados obtenidos.
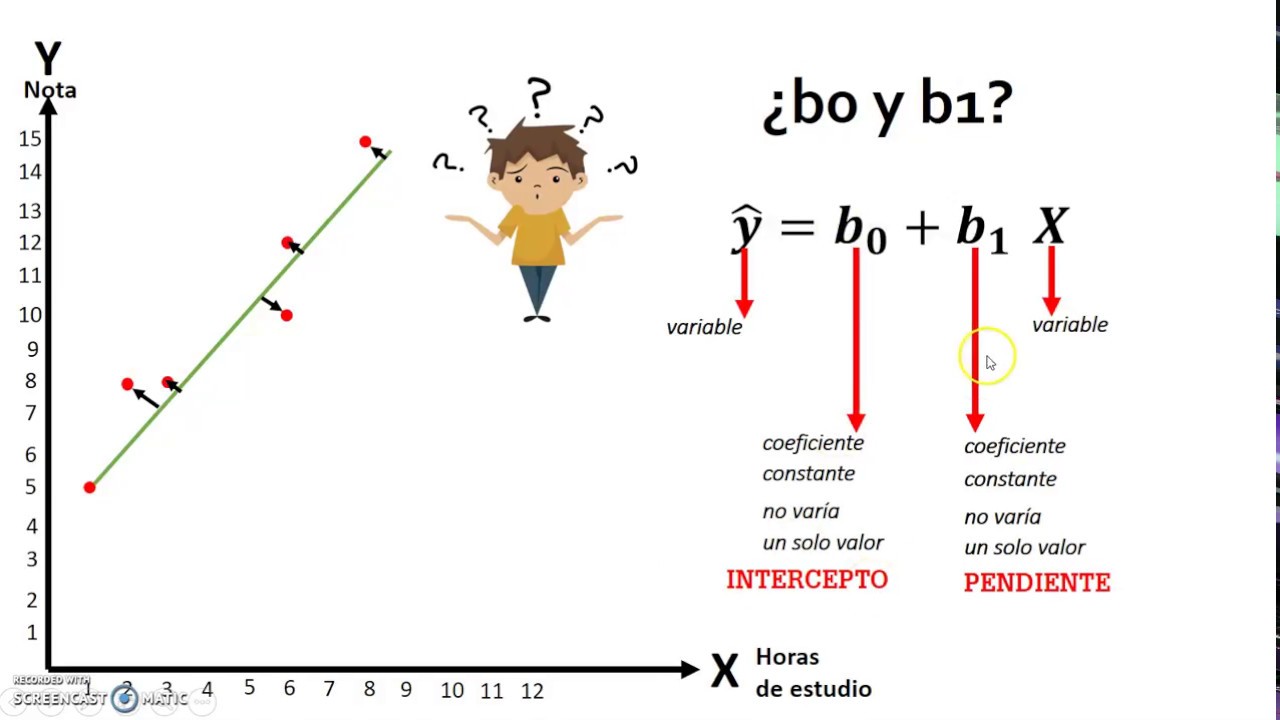
¿Qué diferencia a la regresión múltiple de la regresión simple?
-La regresión múltiple involucra una variable dependiente y múltiples variables independientes, mientras que la regresión simple se centra en la relación entre una sola variable dependiente y una única variable independiente.
¿Qué ejemplos se utilizaron para explicar la regresión múltiple en la clase?
-Se usó como ejemplo el rendimiento de un vehículo en función de su peso y la capacidad de los cilindros, y también se analizó la resistencia de un pegamento en relación con la fuerza, potencia, temperatura y tiempo.
¿Qué es el coeficiente de determinación R² ajustado y por qué es importante?
-El coeficiente de determinación R² ajustado mide la proporción de variabilidad en la variable dependiente que es explicada por las variables independientes. Es importante porque ajusta el R² para el número de variables en el modelo, evitando interpretaciones engañosas.
¿Qué implican los valores p en la prueba de hipótesis de regresión múltiple?
-Los valores p indican si los coeficientes de las variables independientes son significativamente diferentes de cero. Un valor p menor que un nivel alfa (0,05 en este caso) sugiere que la variable tiene un efecto significativo en la variable dependiente.
¿Cómo se determinó si se podía ajustar un modelo de regresión a los datos del pegamento?
-Se realizó una prueba de hipótesis donde la hipótesis nula afirmaba que no había correlación múltiple. Se encontró un valor p muy bajo, lo que llevó a rechazar la hipótesis nula y concluir que sí existe relación múltiple.
¿Qué variables independientes fueron significativas en el modelo de regresión final?
-Las variables significativas en el modelo final fueron la potencia y la temperatura, ya que sus coeficientes fueron diferentes de cero. La fuerza y el tiempo fueron descartados como no significativos.
¿Cuál es la ecuación de regresión final derivada del análisis?
-La ecuación de regresión final es Y = -24.900 + 0.498 * (potencia) + 0.130 * (temperatura), donde Y representa la resistencia del pegamento.
¿Qué resultados se obtuvieron al aplicar la ecuación de regresión con valores específicos?
-Al aplicar la ecuación con potencia igual a 100 y temperatura igual a 170, se obtuvo una resistencia de 46.998.
¿Qué papel juega el análisis de varianza (ANOVA) en la regresión múltiple?
-El análisis de varianza (ANOVA) se utiliza para determinar si al menos una de las variables independientes tiene un efecto significativo sobre la variable dependiente, ayudando a validar la regresión múltiple.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahora5.0 / 5 (0 votes)