Weibull Distribution and Moment generating function (mgf) of Weibull Distribution in statistics|
Summary
TLDRThis video delves into the Weibull distribution, a vital concept in probability theory. It introduces the characteristics of continuous random variables, focusing on the three parameters that define the Weibull distribution: alpha, beta, and mu. The probability density function is explained in detail, highlighting its significance in statistical analysis. Additionally, the moment-generating function is discussed, illustrating how it relates to expectations. The presentation aims to enhance understanding of continuous distributions, making complex statistical concepts accessible and engaging for viewers.
Takeaways
- 📈 The script discusses the concept of distributions in probability theory, focusing on continuous random variables.
- 🎯 It introduces the overall distribution characterized by three parameters: mean (mu), scale (beta), and shape (alpha).
- 🔍 The probability density function (PDF) for the given distribution is defined as f(x) = (x - mu) / (beta * alpha).
- 📊 The Evil distribution is mentioned, highlighting its importance in statistical modeling.
- 💡 The moment-generating function (MGF) of the distribution is given by M_X(t) = E[e^(tX)], linking moments to expectations.
- 📉 The expectations for the distribution are critical for understanding its properties and behavior.
- 🎶 The script includes various musical interludes, potentially signifying transitions between topics.
- 🔗 The discussion includes comparisons to other distributions, indicating the context of the overall distribution in statistical theory.
- ⚙️ The parameters alpha and beta are emphasized as essential for defining the characteristics of the distribution.
- 🔄 The importance of understanding continuous processes in probability is underscored, paving the way for deeper insights into statistical distributions.
Q & A
What is the Weibull distribution used for?
-The Weibull distribution is primarily used in reliability engineering and failure analysis to model the time until an event occurs, such as equipment failure.
What are the key parameters of the Weibull distribution?
-The Weibull distribution has two key parameters: alpha (α), the shape parameter, and beta (β), the scale parameter.
How does the shape parameter (alpha) affect the Weibull distribution?
-The shape parameter (α) influences the failure rate over time. If α < 1, the failure rate decreases; if α = 1, it corresponds to a constant failure rate; and if α > 1, the failure rate increases over time.
What is the probability density function (PDF) of the Weibull distribution?
-The PDF of the Weibull distribution is given by: f(x; α, β) = (α/β) * (x/β)^(α - 1) * e^(-(x/β)^(α)) for x ≥ 0, where α > 0 and β > 0.
What does the scale parameter (beta) represent in the Weibull distribution?
-The scale parameter (β) stretches or compresses the distribution along the x-axis, affecting the scale of the data being modeled.
What is the moment-generating function (MGF) for the Weibull distribution?
-The moment-generating function (MGF) is expressed as M_X(t) = E[e^(tX)], which helps to find the moments of the distribution, such as the mean and variance.
What happens to the Weibull distribution when alpha equals 1?
-When α equals 1, the Weibull distribution simplifies to the exponential distribution, which has a constant failure rate.
How can the expected value and variance of the Weibull distribution be computed?
-The expected value and variance of the Weibull distribution can be computed using formulas that incorporate the parameters α and β, although they are typically expressed in terms of these parameters.
Why is the Weibull distribution considered versatile?
-The Weibull distribution is considered versatile because it can model various types of failure data, adapting its shape to different scenarios based on the value of its parameters.
Can the Weibull distribution model both increasing and decreasing failure rates?
-Yes, depending on the value of the shape parameter α, the Weibull distribution can model both increasing (α > 1) and decreasing (α < 1) failure rates.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Distribusi Chi-square, Weibull, t dan F

Metode Statistika | Sebaran Peluang Kontinu | Mengenal Sebaran Normal

Distribusi Binomial • Part 6: Contoh Soal Distribusi Peluang Variabel Acak Diskrit (3)

Distribusi Binomial • Part 9: Distribusi Peluang Binomial

DOE Part 1
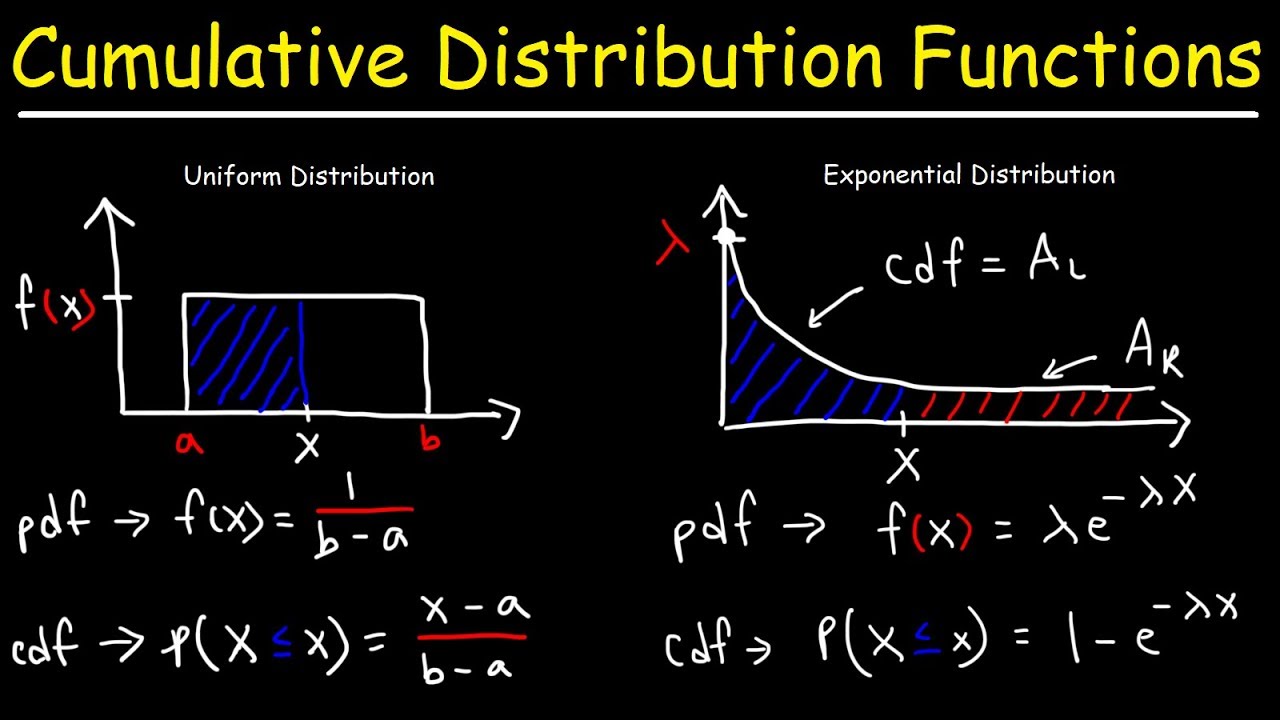
Cumulative Distribution Functions and Probability Density Functions
5.0 / 5 (0 votes)
