Discrete Fourier Transform - Simple Step by Step
Summary
TLDRThis video explains the Fourier series and Fourier transform, which are essential tools for analyzing signals in the time and frequency domains. It illustrates how a complex time-domain signal, such as white noise, can be decomposed into its frequency components using these mathematical concepts. By employing the discrete Fourier transform (DFT), the video simplifies the calculation of frequency coefficients, emphasizing the use of complex exponentials. An example with a 1 Hz sine wave showcases how to interpret frequency and phase information, highlighting the significance of sampling rates in accurate signal representation.
Takeaways
- 😀 The Fourier series decomposes periodic functions into a constant and a series of sine and cosine functions.
- 😀 A white noise signal in the time domain appears chaotic, but its frequency domain representation is a straight line due to equal representation of all frequencies.
- 😀 The Fourier transform allows us to calculate coefficients for each frequency, revealing how much of each sinusoid is present in a signal.
- 😀 Using complex exponentials in the Fourier transform simplifies calculations compared to using real sines and cosines.
- 😀 In practice, we often work with discrete data collected over a finite time, necessitating the use of the discrete Fourier transform (DFT).
- 😀 The DFT involves summing over a finite number of samples to determine frequency coefficients within defined frequency bins.
- 😀 Euler's formula helps expand complex exponentials into sine and cosine terms, aiding in signal analysis.
- 😀 The magnitude of a complex number represents the amplitude of the sinusoid at a given frequency, while the angle provides phase information.
- 😀 In an example of a 1 Hz sine wave, the Fourier transform confirms the expected amplitude and phase, demonstrating practical applications of theory.
- 😀 The Nyquist limit determines the maximum frequency that can be accurately represented, necessitating careful consideration of sampling rates.
Q & A
What is the Fourier series used for?
-The Fourier series is used to decompose any periodic function into a sum of a constant and a series of sines and cosines, allowing analysis of its frequency components.
How does white noise appear in the time domain?
-In the time domain, white noise appears as an erratic and unpredictable signal, which represents the amplitude fluctuations over time.
What does the frequency domain representation of white noise look like?
-In the frequency domain, white noise is represented as a straight line, indicating that each frequency from 20 Hertz to 20,000 Hertz is equally represented.
Why is real-world white noise not perfectly represented in the frequency domain?
-Real-world white noise is not perfectly represented due to the non-ideal characteristics of recording sensors, which are not equally sensitive to all frequencies.
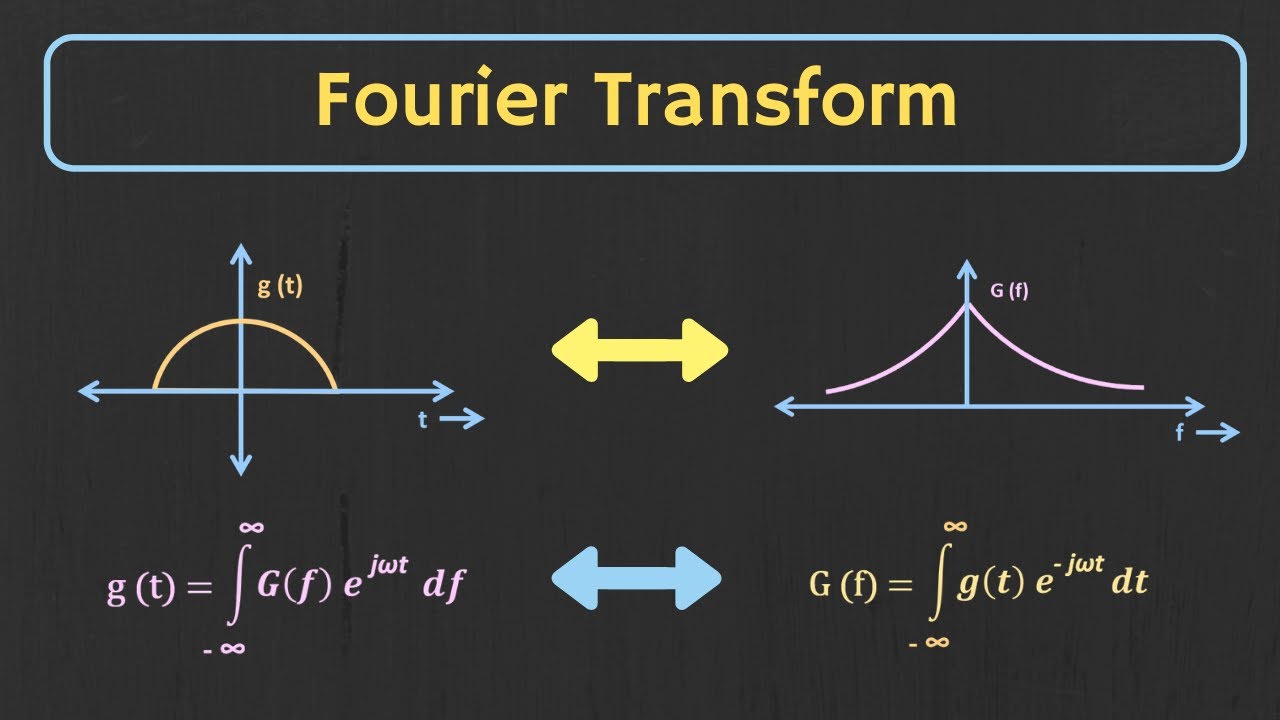
What is a Fourier transform and how is it related to calculating frequency coefficients?
-A Fourier transform is a mathematical operation that transforms a time-domain signal into its frequency components, allowing calculation of coefficients for each frequency.
What is the difference between a continuous Fourier transform and a discrete Fourier transform?
-A continuous Fourier transform analyzes signals over continuous time, while a discrete Fourier transform evaluates signals based on discrete sample points collected over a finite time frame.
What is Euler's formula and how is it applied in the context of Fourier transforms?
-Euler's formula states that e^(jx) = cos(x) + j sin(x), and it is used to convert complex exponentials in Fourier transforms into sums of sine and cosine functions.
What information can be derived from the complex number obtained from a Fourier transform?
-From the complex number, one can derive the magnitude, which corresponds to the amplitude of the sinusoid at that frequency, and the phase, which indicates the phase shift of the sinusoid.
What happens to the frequency coefficients calculated from a signal with an amplitude of 1 Hertz?
-When a 1 Hertz sine wave is analyzed, the Fourier transform should yield a coefficient indicating an amplitude value at the 1 Hertz frequency bin, while other bins should ideally be zero.
How do the Nyquist limit and frequency bins affect frequency resolution in a Fourier transform?
-The Nyquist limit, defined as half the sampling frequency, determines the maximum frequency that can be accurately measured. Frequency resolution is affected by the number of samples and the sampling frequency, defining how closely spaced the frequency bins are.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
Fourier Transform Explained

Pengolahan Sinyal Digital: 09 Transformasi Fourier, STFT & Wavelet Transform

What is Continuous Wavelet Transform (CWT)? | Wavelet Theory | Advanced Digital Signal Processing

Module 1: Time vs Frequency Domains

I Prodigi della TRASFORMATA di FOURIER

What is the Fourier Transform used for?
5.0 / 5 (0 votes)
