79. Funciones linealmente independientes ¿qué son? CON EJEMPLOS
Summary
TLDREn este video de Mate, fácil, se exploran las soluciones linealmente independientes de las ecuaciones diferenciales lineales de segundo orden. Se define la independencia lineal y se ejemplifica mediante diferentes funciones, mostrando cómo se pueden multiplicar por constantes sin que una funcione como múltiplo de la otra. Además, se discute el concepto de la solución general de estas ecuaciones, la cual se forma combinando dos soluciones linealmente independientes. El video concluye invitando a los espectadores a interactuar y a seguir aprendiendo sobre este tema fundamental en matemáticas.
Please replace the link and try again.
Please replace the link and try again.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
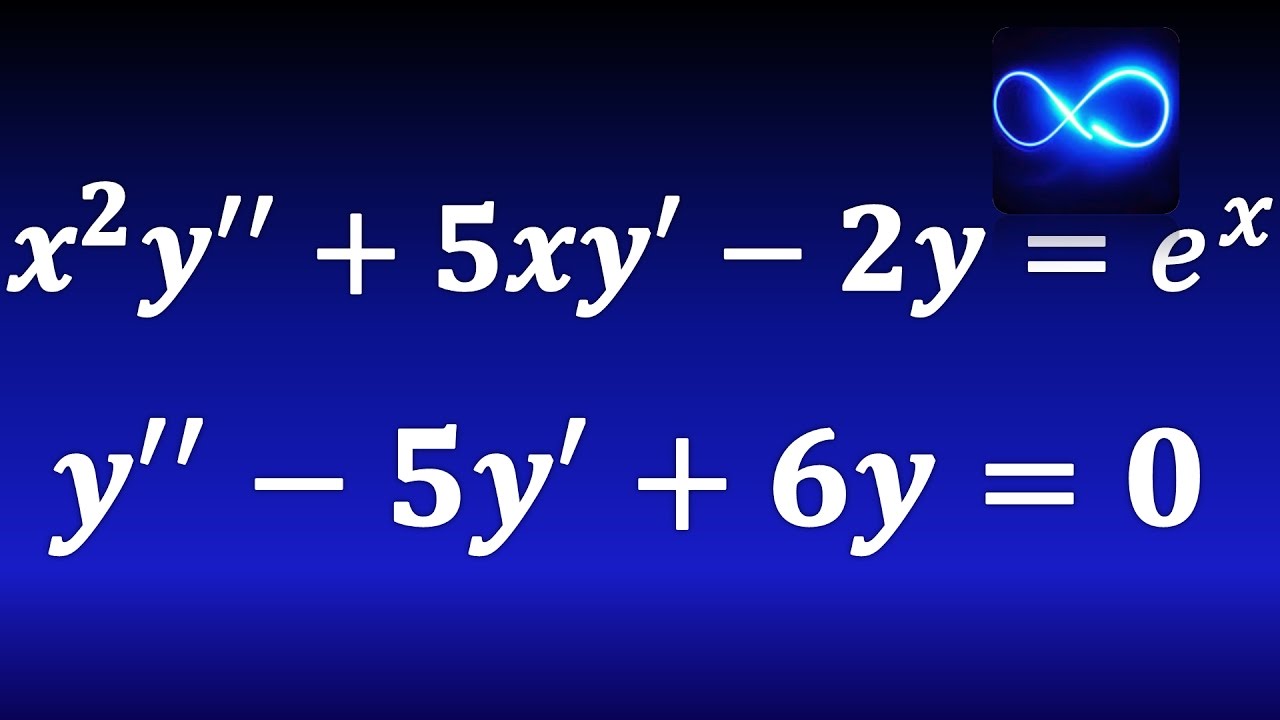
78. Qué son las ecuaciones de segundo orden, ecuaciones homogéneas y de coeficientes constantes
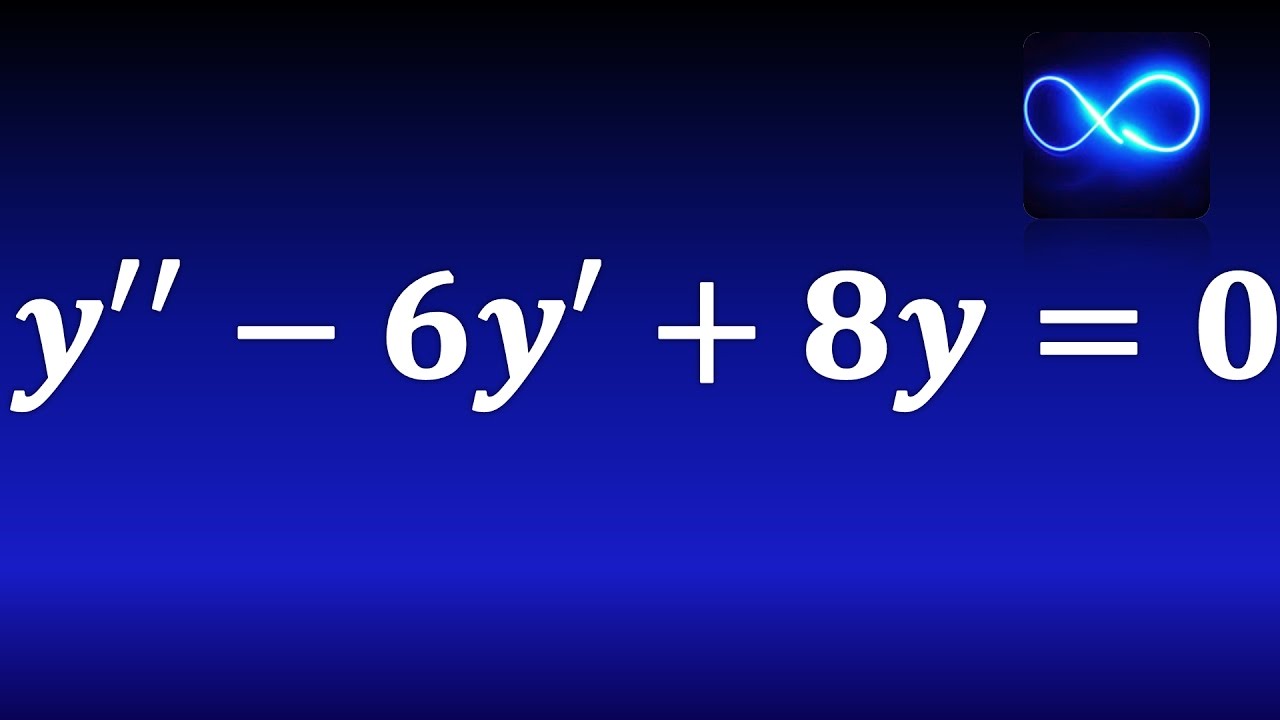
86. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO
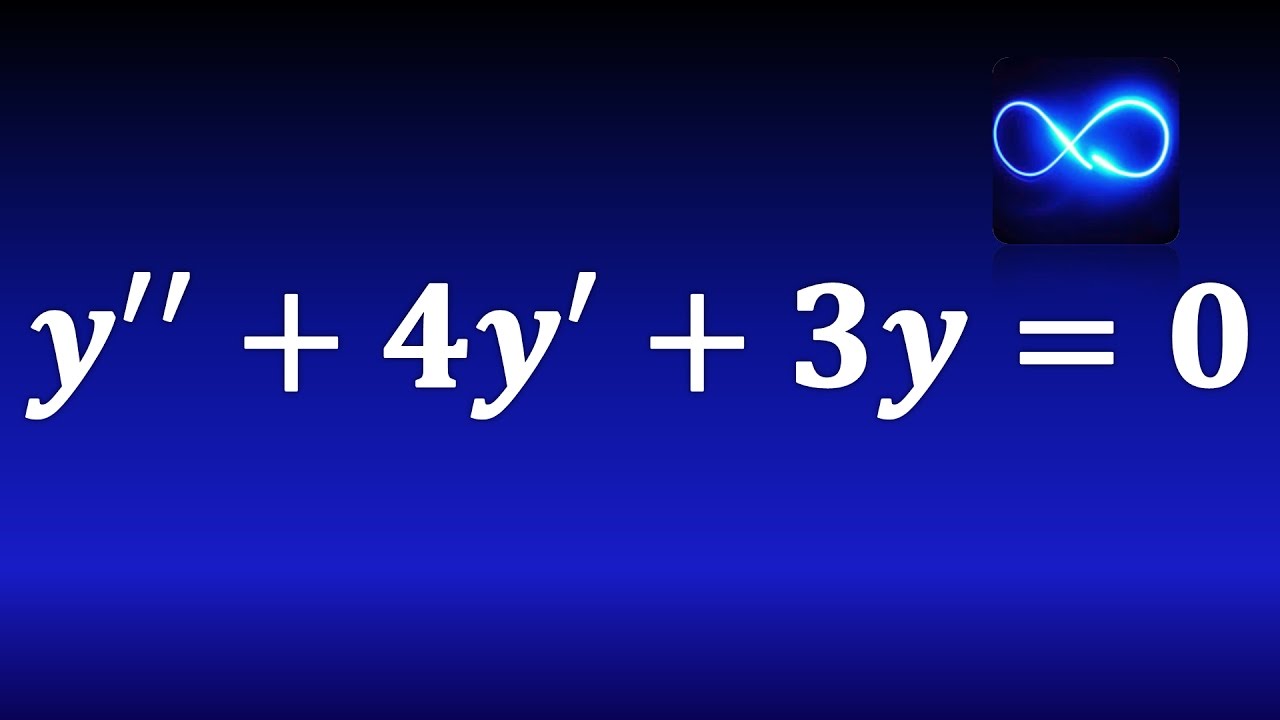
87. Ecuación diferencial de coeficientes constantes (segundo orden, homogénea) EJERCICIO RESUELTO

ECUACIONES DE SEGUNDO GRADO: completas e incompletas

Orden de una Ecuación Diferencial

Ecuaciones diferenciales | Introducción
5.0 / 5 (0 votes)