8. METODE LELARAN TITIK TETAP - FIX POINT ITERATION - METODE NUMERIK
Summary
TLDRIn this video, the presenter continues the discussion on solving non-linear equations using open methods, following a review of the bisection and false position methods. The focus is on fixed-point iteration, Newton-Raphson, and the secant method to determine the next values of x. Various functions are explored to approximate solutions for the equation x² - 2x - 3 = 0, with a tolerance of 0.000001. The presenter explains convergence criteria through derivatives, assessing which functions can be effectively utilized. The video aims to guide viewers through the iterative process of finding accurate solutions.
Takeaways
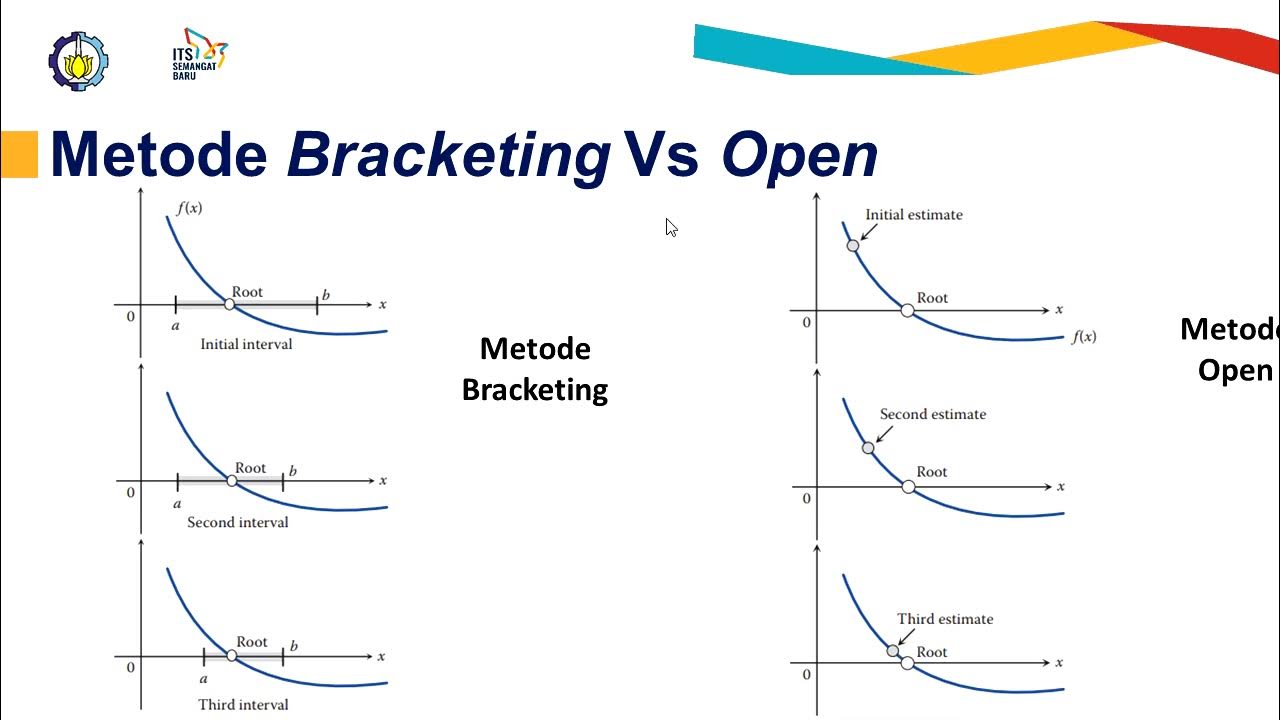
- 😀 The video continues the discussion on solutions to nonlinear equations using open methods, building on previous methods like bisection and false position.
- 😀 The open methods determine the next value of x by forming a function gx from the original equation.
- 😀 Initial guesses for x start from a specified value (e.g., 0, 1, 2, 3) and the process stops when the difference between the current and previous x values is less than a set tolerance.
- 😀 Three methods are discussed: Fixed Point Iteration, Newton-Raphson, and the Second Method.
- 😀 The example given involves solving the equation x² - 2x - 3 = 0 with a tolerance of 0.00000123 using Fixed Point Iteration.
- 😀 Multiple forms of the function gx are derived, including gx = sqrt(2x + 3), gx = 3/(x-2), and gx = (x² - 3)/2.
- 😀 To determine the convergence or divergence of the methods, derivatives of the functions are evaluated.
- 😀 A function is convergent if its derivative is between 0 and -1, convergent oscillating between -1 and 0, and divergent if it exceeds these ranges.
- 😀 For the first function, checking the derivative at specific values (x = 0 and x = 1) shows that it converges monotonically.
- 😀 The determination of x values will be further processed in Microsoft Excel to find the solution within the given tolerance.
Q & A
What is the main focus of the video?
-The video focuses on solutions for nonlinear equations using open methods, following a previous discussion on closed methods like the bisection method and the false position method.
What are the three open methods discussed in the video?
-The three open methods discussed are the fixed-point iteration method, the Newton-Raphson method, and a third unspecified method.
How is the initial guess for the value of x determined?
-The initial guess for x is determined freely, starting from values such as 0, 1, 2, 3, and so on.
What condition must be met for the iterative process to stop?
-The iterative process stops when the absolute difference between the current x value and the previous x value is less than the specified tolerance.
How is the function gx formed for the fixed-point iteration method?
-The function gx is formed by rearranging the original equation, such as isolating x on one side, to derive a new function that can be iteratively evaluated.
What is the tolerance level used in the example provided?
-The tolerance level used in the example is 0.00000123.
What determines whether a function's iteration is convergent or divergent?
-The convergence or divergence of a function's iteration is determined by the derivative of the function. If the derivative lies between 0 and 1, it converges monotonically; between -1 and 0 indicates oscillating convergence, while values outside these ranges indicate divergence.
What is the significance of the derivative in assessing the three derived functions?
-The significance of the derivative is to evaluate whether the iterations for each derived function will converge or diverge, thus determining their suitability for finding the root of the equation.
What is the example function used to illustrate the fixed-point iteration method?
-The example function used is x^2 - 2x - 3 = 0, which is transformed into different forms for iterative evaluation.
What is the final outcome discussed regarding the checks for the values of x?
-The final outcome discusses that the values of x will be verified in Microsoft Excel, and further steps will be outlined in the next video.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
Fisika Komputasi 1: Metode-metode Akar persamaan Secara Numerik

Finalizando a semana 3

Matrices (cayley Hamiton Theorem) IN HINDI Part No 04 As Per New Syllabus (N O C )

5 MTK EKO PENCARIAN AKAR AKAR PERS LINEAR

S. Y. B. SC. (Comp.Sci.) (Paper - II: Numerical Techniques) Ch1-Algebraic & Transcendental Eq.(Lec1)

SPtDV • Part 3: Cara Menentukan Pertidaksamaan Dua Variabel dari Grafik Daerah Penyelesaian
5.0 / 5 (0 votes)
