HALLAR LA EXCENTRICIDAD Y LA ECUACIÓN DE UNA ELIPSE
Summary
TLDREn este video, se aborda la resolución de un problema matemático relacionado con la excentricidad de una elipse centrada en el origen. Se detalla la ubicación de los vértices y la formulación de la ecuación canónica de la elipse. A través de cálculos y simplificaciones, se determina la relación entre los ejes y se encuentra el valor de 'b'. Finalmente, se calcula la excentricidad de la elipse, presentando un resultado aproximado. Este tutorial ofrece un enfoque paso a paso, ideal para estudiantes que buscan comprender conceptos de geometría de manera clara y efectiva.
Takeaways
- 😀 La elipse tiene su centro en el origen (0, 0) y uno de sus vértices en (0, -7).
- 😀 El eje mayor de la elipse es vertical, ya que uno de los vértices se encuentra en el eje y.
- 😀 La distancia desde el centro hasta un vértice (a) es igual a 7, lo que significa que la longitud total del eje mayor es 14.
- 😀 La ecuación canónica de la elipse es de la forma x²/b² + y²/a² = 1.
- 😀 Dado que el valor de a es 7, se establece que a² = 49 en la ecuación canónica.
- 😀 Para encontrar b, se sustituye un punto conocido (√5, 14/3) en la ecuación canónica.
- 😀 Se simplifica la ecuación resultante para despejar b², obteniendo b² = 9.
- 😀 Por lo tanto, b = 3, que representa la distancia desde el centro hasta un vértice del eje menor.
- 😀 La excentricidad (e) de la elipse se calcula usando la fórmula e = √(a² - b²)/a.
- 😀 La excentricidad resultante es aproximadamente 0.9, lo que indica la forma de la elipse.
Please replace the link and try again.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Geometría Analítica: Ecuación de la elipse dados foco y la excentricidad.

Resolución de un problema de suma llevada 1º de Primaria

Matemáticas 17 ICFES 2014
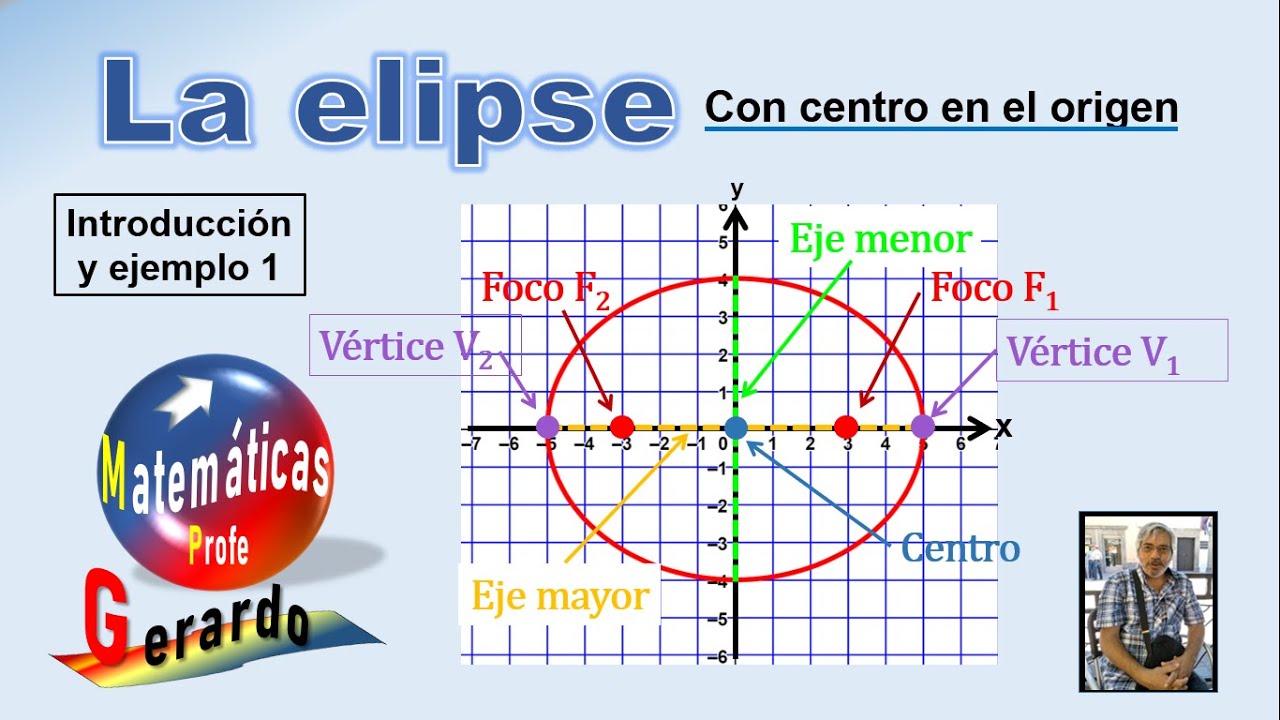
La elipse con centro en el origen. Introducción y ejemplo 1.

63. Encontrar a todos los elementos de una elipse cuando te dan su ecuación general.

Volumen con despeje ( Cilindro)
5.0 / 5 (0 votes)