Área entre dos funciones. Cálculo integral.
Summary
TLDREn este video, el profesor de matemáticas explica cómo calcular el área encerrada entre dos funciones utilizando cálculo integral. A través de gráficos, se ilustra el concepto de área entre las curvas, y se muestran los pasos para encontrar los puntos de intersección y establecer la integral definida. El profesor destaca la importancia de restar las funciones para obtener la función diferencia y explica cómo evaluar la integral para encontrar el área. Al final, se refuerza que el valor absoluto de la función diferencia se puede usar para asegurar resultados positivos en el cálculo del área, y se invita a los espectadores a explorar más recursos en su página web.
Takeaways
- 😀 Se enseña cómo calcular el área entre dos funciones utilizando cálculo integral.
- 📈 Es importante representar gráficamente las funciones para entender el área encerrada.
- 🟡 La función cuadrática y la función lineal se utilizan como ejemplos para el cálculo del área.
- ✏️ La integral definida se usa para calcular el área entre las curvas de las funciones.
- 🔢 Se necesita encontrar los puntos de intersección de las funciones para determinar los límites de la integral.
- 📐 La diferencia entre las funciones (f(x) - g(x)) se integra para encontrar el área.
- 🔍 Se utilizan ecuaciones de segundo grado para resolver los puntos de intersección.
- ⚙️ La evaluación de la integral se realiza en los límites encontrados para calcular el área.
- 📊 El resultado del área puede expresarse tanto en fracciones como en decimales.
- 💡 Es relevante entender que el valor absoluto de la función diferencia garantiza un área positiva, independientemente del orden de las funciones.
Q & A
¿Cuál es el objetivo principal de este video?
-El objetivo principal es aprender a calcular el área encerrada entre dos funciones.
¿Qué método se utiliza para calcular el área entre dos curvas?
-Se utiliza el cálculo integral, específicamente la integral definida de la diferencia entre las dos funciones.
¿Qué se representa gráficamente antes de realizar los cálculos?
-Se representan gráficamente las dos funciones para entender el área que se quiere calcular.
¿Cómo se determina la función que está arriba y la que está abajo?
-Se analiza el gráfico de las funciones y se identifica cuál está por encima del eje x y cuál está por debajo.
¿Cuál es la ecuación que se obtiene al restar las dos funciones?
-La ecuación obtenida es fx - gx, que en este caso se traduce en -x² - 2x + 3.
¿Cómo se encuentran los límites de integración?
-Los límites se encuentran resolviendo el sistema de ecuaciones donde las funciones se cortan.
¿Qué pasos se siguen para calcular la integral definida?
-Se evalúan las integrales de cada término en los límites determinados, restando el valor inferior del superior.
¿Qué sucede si se toma la función inferior primero en la resta?
-Si se toma la función inferior primero, el resultado será negativo, pero el valor absoluto se utiliza para que el área sea positiva.
¿Cuál es el resultado final del área calculada entre las dos funciones?
-El área encerrada entre las dos funciones es de 10.67 unidades cuadradas.
¿Qué recursos adicionales se ofrecen al final del video?
-Se menciona que se pueden encontrar más videos, ejercicios y material educativo en la página web todosobresaliente.com.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
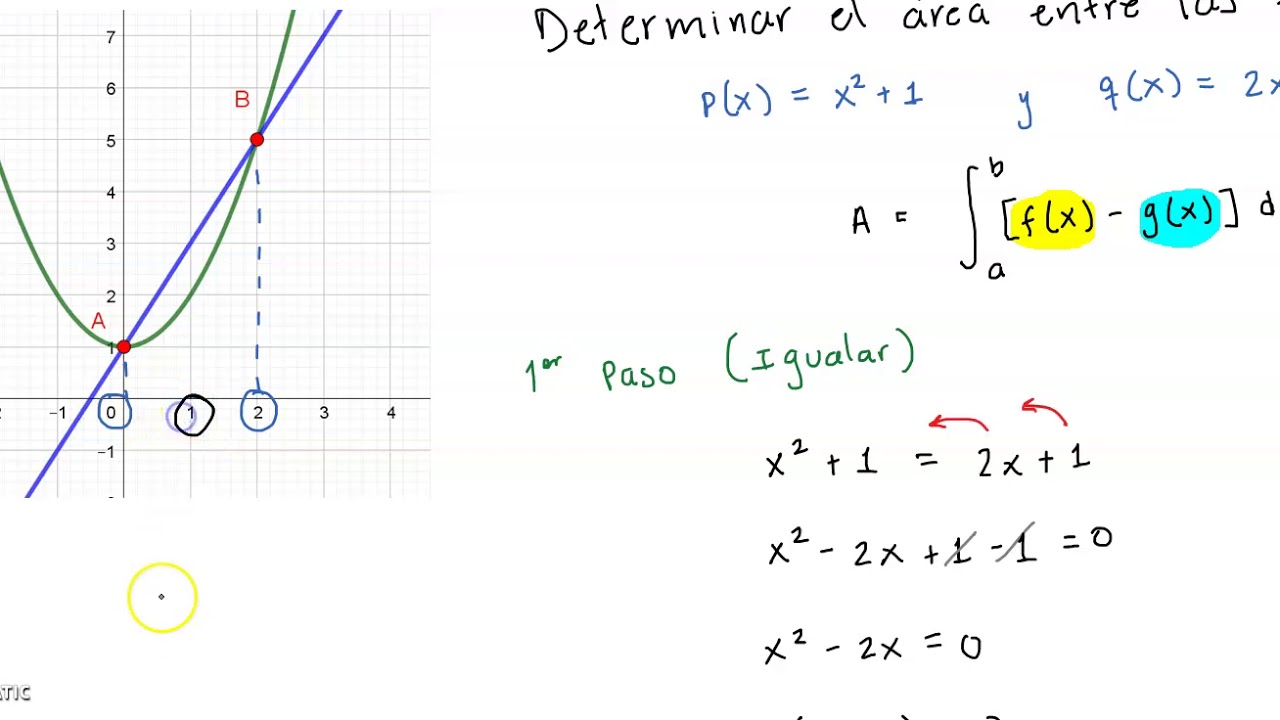
AREA ENTRE CURVAS EJEM1

AREA ENTRE CURVAS INTRO

INTEGRALI - introduzione al calcolo integrale _ NT03
Área de una región plana utilizando sumatorias

Introducción al cálculo integral | Khan Academy en Español

Cálculo Integral 01:Área bajo una curva. Area under a curve
Cálculo del Volumen de una Pirámide de Base Cuadrada
5.0 / 5 (0 votes)