Venn Diagram Word Problems With 3 Categories
Summary
TLDRThe video provides a detailed explanation of solving Venn diagram word problems involving three categories. The instructor walks through a class example where students study algebra, biology, and chemistry. By breaking down the problem into sections and using a Venn diagram, the speaker solves for how many students are studying specific combinations of subjects. Another example involves students owning cats, dogs, and parrots. The video emphasizes the step-by-step approach to calculating values for various intersections and totals in a clear and systematic way, making complex problems more approachable.
Takeaways
- 🧮 The problem involves a Venn diagram with three categories: algebra, biology, and chemistry, and breaks down the number of students studying each combination of subjects.
- 🔟 Ten students are studying all three subjects: algebra, biology, and chemistry.
- 🧑🏫 Part A: 7 students are studying both algebra and biology, but not chemistry.
- 👩🔬 Part B: 5 students are studying both biology and chemistry, but not algebra.
- 🧑🔬 Part C: 8 students are studying both algebra and chemistry, but not biology.
- 📘 Part D: 21 students are studying only algebra, excluding biology and chemistry.
- 📗 Part E: 17 students are studying only biology.
- 📙 Part F: 14 students are studying only chemistry.
- 📚 The total number of students surveyed is 100, including those who are not studying any of the three subjects.
- 📝 The solution involves systematic subtraction and addition of overlapping sections in the Venn diagram to find specific subsets of students.
Q & A
Question 1: How do you determine the number of students studying Algebra and Biology but not Chemistry?
-To find the number of students studying Algebra and Biology but not Chemistry, subtract the number of students studying all three subjects from those studying Algebra and Biology. In this case, it's 17 students studying Algebra and Biology, and 10 of them are also studying Chemistry. Therefore, 17 - 10 = 7 students are studying Algebra and Biology but not Chemistry.
Question 2: What is the method to calculate how many students are studying Biology and Chemistry but not Algebra?
-To calculate how many students are studying Biology and Chemistry but not Algebra, subtract the number of students studying all three subjects from those studying Biology and Chemistry. In this case, 15 students are studying Biology and Chemistry, and 10 of them are also studying Algebra. Therefore, 15 - 10 = 5 students are studying Biology and Chemistry but not Algebra.
Question 3: How do you find the number of students studying Algebra and Chemistry but not Biology?
-To find the number of students studying Algebra and Chemistry but not Biology, subtract the number of students studying all three subjects from those studying Algebra and Chemistry. Here, 18 students are studying Algebra and Chemistry, and 10 of them are also studying Biology. So, 18 - 10 = 8 students are studying Algebra and Chemistry but not Biology.
Question 4: How is the number of students studying only Algebra calculated?
-The number of students studying only Algebra is found by subtracting the number of students studying Algebra alongside other subjects from the total number of Algebra students. Here, the total number is 46, and we subtract those studying Algebra and Biology (7), Algebra and Chemistry (8), and all three subjects (10). So, 46 - 7 - 8 - 10 = 21 students are studying only Algebra.
Question 5: How do you calculate the number of students studying only Biology?
-To calculate the number of students studying only Biology, subtract the students studying Biology alongside other subjects from the total number of Biology students. The total number is 39, and we subtract those studying Algebra and Biology (7), Biology and Chemistry (5), and all three subjects (10). So, 39 - 7 - 10 - 5 = 17 students are studying only Biology.
Question 6: What is the method for finding how many students are studying only Chemistry?
-The number of students studying only Chemistry is found by subtracting the number of students studying Chemistry alongside other subjects from the total number of Chemistry students. The total number is 37, and we subtract those studying Algebra and Chemistry (8), Biology and Chemistry (5), and all three subjects (10). So, 37 - 8 - 5 - 10 = 14 students are studying only Chemistry.
Question 7: How many students in total were surveyed in this class of sophomores?
-To find the total number of students surveyed, add all the students studying different combinations of subjects along with those who study none. Adding the numbers (21 + 7 + 8 + 10 + 5 + 17 + 14) gives 82 students studying at least one subject, plus 18 students studying none, resulting in a total of 100 students surveyed.
Question 8: How do you determine the number of students studying Algebra or Biology?
-To determine how many students are studying Algebra or Biology, add all the students studying any combination of Algebra or Biology. This includes those studying only Algebra (21), only Biology (17), both Algebra and Biology but not Chemistry (7), both Algebra and Chemistry but not Biology (8), both Biology and Chemistry but not Algebra (5), and those studying all three subjects (10). The total is 21 + 7 + 8 + 10 + 5 + 17 = 68 students studying Algebra or Biology.
Question 9: How is the number of students studying Biology or Chemistry calculated?
-To calculate how many students are studying Biology or Chemistry, add all the students studying any combination of Biology or Chemistry. This includes those studying only Biology (17), only Chemistry (14), both Biology and Chemistry but not Algebra (5), both Biology and Algebra but not Chemistry (7), both Algebra and Chemistry but not Biology (8), and those studying all three subjects (10). The total is 17 + 7 + 8 + 10 + 5 + 14 = 61 students studying Biology or Chemistry.
Question 10: What is the significance of using a Venn diagram in solving these word problems?
-A Venn diagram helps visualize the overlap between different categories, making it easier to identify how many students fall into specific combinations of groups, such as those studying multiple subjects. It breaks down complex relationships into manageable parts, allowing for systematic calculations based on the given data.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Venn Diagrams with 3 Circles
Economic, environmental and social sustainability: Sustainable Development - Jon Erik Dahlin

Pengertian Sistem Persamaan Linear Tiga Variabel

KALKULUS | Sistem Bilangan Real - Part 4 | Pertidaksamaan

Statika Partikel 3D (5/5): Kesetimbangan Partikel dalam Tiga Dimensi
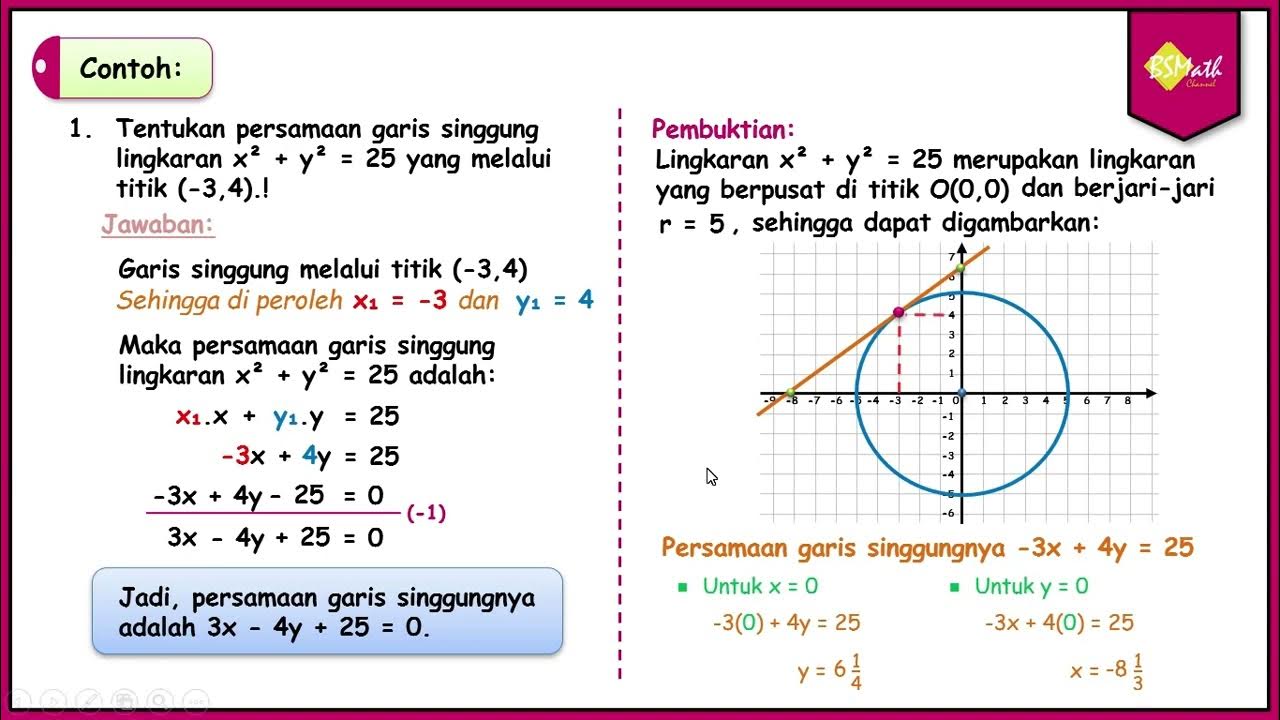
Persamaan Garis Singgung Lingkaran di Suatu Titik Pada Lingkaran - SMA Kelas XI Kurikulum Merdeka
5.0 / 5 (0 votes)
