1's and 2's Complement

Summary

This lecture covers key concepts of one's and two's complement in number systems. The instructor explains how to calculate one's complement by subtracting a binary number from all ones, then demonstrates this process with examples, including how NOT gates work in generating the complement. The two's complement is introduced by first calculating one's complement and then adding one to it. The lecture ends with two homework problems: finding one's complement of a given number and calculating two's complement for another. A shortcut method for finding two's complement is promised for the next session.

Takeaways

• 📘 One's complement can be obtained by subtracting a binary number from a sequence of all ones.
• 📊 The expression for one's complement is R^n - 1 - N, where R is the radix and N is the given number.
• 🔢 For a base 10 system, the result of the one's complement formula gives a number with all digits as 9.
• 🔢 For a base 8 system, the result gives a number with all digits as 7, and for base 16, it results in F's.
• 🔢 For a binary system, the result of one's complement expression is all 1's.
• 🔄 To calculate one's complement for a binary number, subtract the given number from the result of all 1's (same number of bits).
• 📐 The example given finds the one's complement of 1010, which results in 0101.
• 🚪 NOT gates can be used to find the one's complement of a binary number by flipping each bit.
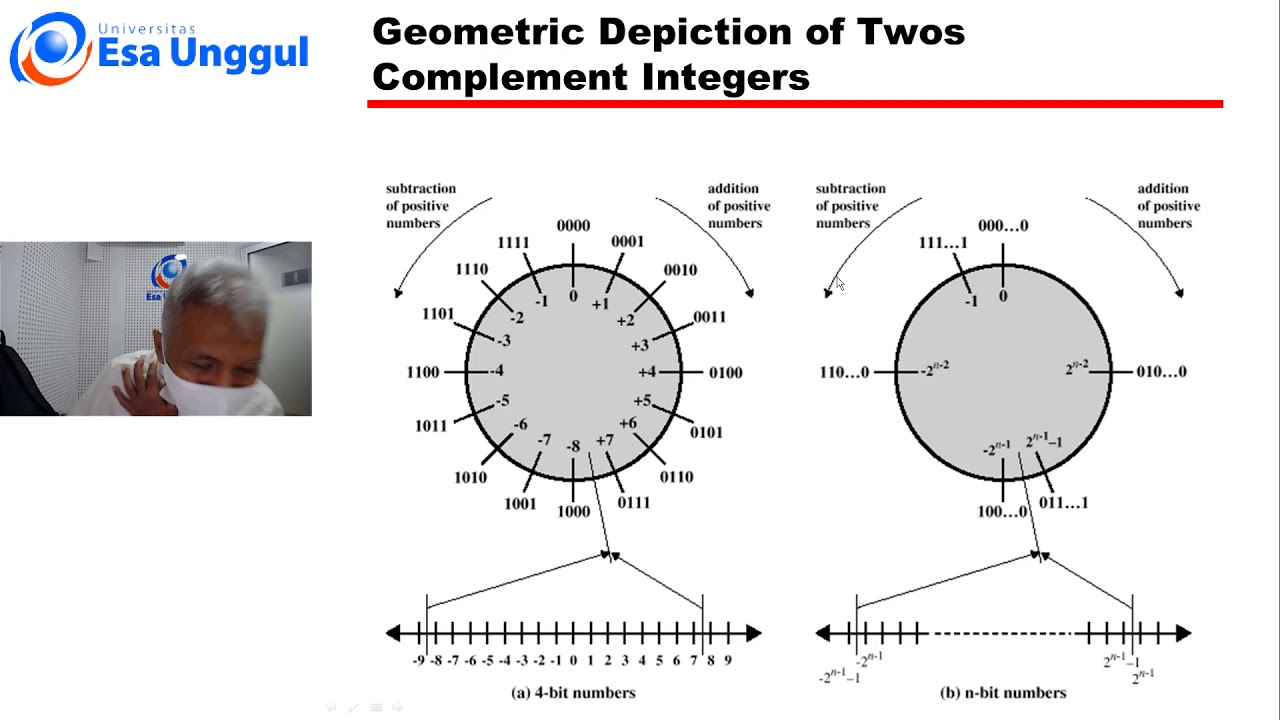
• ➕ To obtain the two's complement, first find the one's complement, then add 1 to it.
• 🏠 Homework problems involve finding the one's complement of 100111 and the two's complement of 1100111.

Q & A

What is the formula used to obtain the one's complement of a binary number?

The one's complement of a binary number is obtained by subtracting the binary number from a series of 1's, which depends on the number of bits (n). The formula is R^n - 1 - N, where R is the base, n is the number of digits, and N is the given number.

What happens when the base (radix) is equal to 2 in the one's complement process?

When the base (radix) is equal to 2, which corresponds to the binary number system, the part of the expression R^n - 1 - N results in a series of 1's equal to the number of digits. For example, for a 4-bit number, the expression will result in 1111.

How is the one's complement of a binary number 1010 calculated in the example?

To calculate the one's complement of 1010, we subtract it from 1111 (a series of four 1's). The subtraction yields 0101 as the one's complement.

What is the function of NOT gates in the context of one's complement calculation?

NOT gates are used to invert the bits of a binary number. For example, in the given example, the input of the NOT gate for 1010 results in the output 0101, which is the one's complement of the given number.

What is the process for calculating the two's complement of a binary number?

To calculate the two's complement, first, find the one's complement of the number, then add 1 to the one's complement. For example, the two's complement of 1011010 is obtained by first calculating the one's complement (0100101) and then adding 1, resulting in 0100110.

What is the two's complement of the binary number 1011010 as calculated in the example?

The two's complement of the binary number 1011010 is 0100110. This is obtained by first calculating the one's complement (0100101) and then adding 1.

What are the homework problems given at the end of the presentation?

The homework problems are: 1) Find the one's complement of 100111, and 2) Find the two's complement of 1100111.

Why is it unnecessary to solve the first part of the expression in one's complement calculation?

It is unnecessary to solve the first part of the expression (R^n - 1) because it always results in a series of identical digits (like 1111 for binary or FFFF for hexadecimal) based on the base or radix, making the actual calculation straightforward.

How is the carry handled in the two's complement calculation?

In two's complement calculations, if 1 + 1 occurs during addition, the result is 0 with a carry of 1, which is then added to the next higher bit.

What will be covered in the next presentation as per the script?

In the next presentation, a shortcut method for calculating the two's complement will be introduced.