Punto Medio de un Segmento. FÁCIL. 2 ejemplos
Summary
TLDREn este video, Giovanna enseña cómo encontrar el punto medio de un segmento utilizando la fórmula correspondiente. A través de ejemplos prácticos, muestra cómo identificar y graficar el punto medio de segmentos formados por dos puntos con coordenadas dadas. Explica detalladamente cómo operar con números positivos y negativos, la importancia de verificar resultados visualmente, y las reglas de los signos en las operaciones. Además, ofrece ejercicios adicionales para practicar y refuerza la importancia de tener un buen entendimiento visual de los resultados.
Takeaways
- 📏 El tema principal es el cálculo del punto medio de un segmento.
- 📝 Se utilizan las coordenadas de dos puntos para formar el segmento: A(-5,7) y B(3,9).
- 📊 Es importante visualizar aproximadamente la ubicación del punto medio antes de calcularlo.
- 🧮 La fórmula para calcular el punto medio es: ((x1 + x2)/2, (y1 + y2)/2).
- ➕ Al sumar un número positivo y un negativo, se resta el valor absoluto más pequeño del más grande, conservando el signo del mayor.
- 🔢 Para el primer ejemplo, las coordenadas del punto medio son (-1, 8).
- 🖍️ Se grafica el punto medio para confirmar que cae en el segmento, verificando visualmente que está en la mitad.
- 📐 Se muestra otro ejemplo con las coordenadas A(-8,3) y B(9,-2).
- ✏️ En el segundo ejemplo, las coordenadas del punto medio son (0.5, -2.5).
- 📚 Se recomienda practicar con otros ejercicios y verificar las respuestas en los comentarios.
Q & A
¿Cuál es el objetivo principal del video?
-El objetivo principal del video es enseñar cómo encontrar el punto medio de un segmento en un plano utilizando las coordenadas de dos puntos.
¿Qué fórmula se utiliza para encontrar el punto medio de un segmento?
-La fórmula utilizada es: ((x1 + x2)/2, (y1 + y2)/2), donde (x1, y1) son las coordenadas del punto A y (x2, y2) las del punto B.
¿Por qué es importante visualizar el punto medio antes de calcularlo?
-Es importante visualizar el punto medio para tener una idea aproximada de su ubicación. Esto ayuda a verificar si el resultado final tiene sentido y si coincide con lo esperado visualmente.
¿Qué error común se debe evitar al sumar coordenadas de signos diferentes?
-Cuando se suman coordenadas de signos diferentes, se debe restar en lugar de sumar y se coloca el signo del número mayor.
¿Qué sucede si el resultado de las coordenadas no cae sobre el segmento visualmente?
-Si el resultado no cae sobre el segmento visualmente, es una señal de que puede haber un error en los cálculos, posiblemente en la manipulación de los signos.
¿Qué ocurre cuando ambas coordenadas son negativas en el cálculo?
-Cuando ambas coordenadas son negativas, se suman y el resultado conserva el signo negativo.
¿Cómo se maneja el signo cuando se dividen números en la fórmula del punto medio?
-Al dividir los números en la fórmula, se aplica la ley de signos: un número negativo dividido por uno positivo da un resultado negativo.
¿Cómo se grafican las coordenadas resultantes del punto medio?
-Se grafica el punto medio colocando la coordenada x en el eje X y la coordenada y en el eje Y. El punto debe estar exactamente en la mitad del segmento que une los puntos A y B.
¿Qué significa 'a ojo de buen cubero' en el contexto del video?
-La expresión 'a ojo de buen cubero' se refiere a hacer una estimación aproximada visual del punto medio antes de realizar los cálculos exactos.
¿Qué recomendación final da la instructora para practicar el cálculo del punto medio?
-La instructora recomienda practicar con ejercicios adicionales y verificar las respuestas, que estarán disponibles en los comentarios del video.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
Coordenadas de un punto que divide a un segmento en una razón dada ejemplo 1 | Geometría - Vitual

37. What is the equation of the line? FULL EXPLANATION

Ecuación de la recta conociendo dos puntos | Ejemplo 1

Rectas paralelas y perpendiculares | Ecuación de la recta | La Prof Lina M3
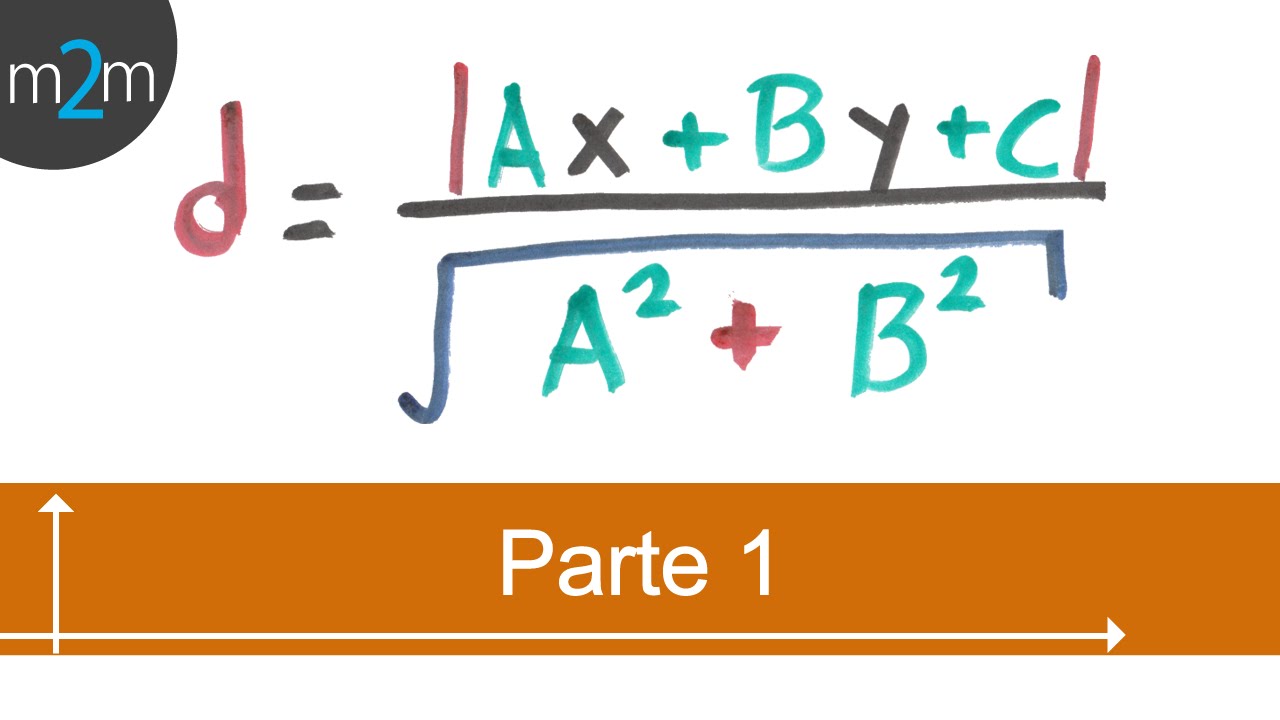
* Distancia entre un punto y una recta (PARTE 1)

DIVISION DE UN SEGMENTO EN UN PUNTO DADO USANDO DECIMAL
5.0 / 5 (0 votes)