Reescribir una integral definida como el límite de una suma de Riemann | Khan Academy en Español
Summary
TLDREn este video se muestra cómo reescribir una integral definida como el límite de una suma de Riemann. El ejemplo utilizado es la integral del coseno entre pi y 2pi, destacando que partes de la integral se cancelan mutuamente. Se explica cómo descomponer el área bajo la curva en rectángulos, calcular su base y altura, y establecer una suma de Riemann por la derecha. El propósito es mostrar cómo aproximar el área bajo una curva mediante rectángulos, mientras el número de divisiones tiende a infinito, logrando una mejor estimación.
Takeaways
- 🧮 Se practica la reescritura de integrales definidas como el límite de una suma de Riemann.
- 📉 El ejemplo utiliza la integral definida de coseno de x, de pi a 2 pi.
- 🎨 Se menciona cómo luce la gráfica del coseno en ese intervalo, con valores específicos en pi y 2 pi.
- ➗ Se descompone el intervalo en n rectángulos para crear la suma de Riemann.
- 📏 La base de cada rectángulo es la diferencia entre los límites de integración, pi y 2 pi, dividida entre n.
- 📐 La altura de los rectángulos se define usando el valor de la función en el extremo derecho de cada subintervalo.
- 🔁 Se utiliza una suma de Riemann por la derecha, calculando alturas en función del valor de la función coseno.
- 📊 La integral definida representa el área entre la curva y el eje x en ese intervalo.
- ⚖️ Se menciona que partes de la integral son negativas y otras positivas, lo que lleva a la cancelación y un valor final de 0.
- 📝 El propósito es expresar la integral como una suma de Riemann tomando el límite cuando n tiende a infinito.
Q & A
¿Qué es una suma de Riemann?
-Una suma de Riemann es un método para aproximar el área bajo una curva al dividir el intervalo de la integral en subintervalos pequeños y sumar las áreas de los rectángulos formados.
¿Cómo se relaciona una suma de Riemann con una integral definida?
-Una integral definida se puede expresar como el límite de una suma de Riemann cuando el número de subintervalos tiende a infinito, lo que hace que la aproximación del área bajo la curva sea más precisa.
¿Qué representa la gráfica del coseno entre π y 2π?
-La gráfica del coseno entre π y 2π va desde -1 en π hasta 1 en 2π, lo que forma una curva que pasa por valores negativos y positivos.
¿Por qué la integral definida entre π y 2π del coseno de x es igual a 0?
-La integral definida es igual a 0 porque las áreas bajo la curva entre π y 2π se cancelan mutuamente: la parte negativa compensa la parte positiva.
¿Cómo se calcula la base de los rectángulos en una suma de Riemann?
-La base de cada rectángulo se calcula tomando la diferencia entre los límites de integración (2π - π) y dividiendo esa diferencia por n, es decir, π/n.
¿Cómo se determina la altura de los rectángulos en una suma de Riemann por la derecha?
-La altura de cada rectángulo se determina evaluando la función en el extremo derecho de cada subintervalo. Por ejemplo, la altura en el primer subintervalo es f(π + π/n).
¿Cuál es la forma general para la altura de los rectángulos en una suma de Riemann por la derecha?
-La forma general de la altura de los rectángulos es f(π + k(π/n)), donde k es el número del subintervalo, y n es el número total de intervalos.
¿Qué sucede con el área de los rectángulos cuando n tiende a infinito?
-Cuando n tiende a infinito, el área de los rectángulos se aproxima cada vez más al área exacta bajo la curva, y la suma de Riemann converge a la integral definida.
¿Cómo se expresa una integral como el límite de una suma de Riemann?
-Una integral se expresa como el límite de una suma de Riemann tomando la suma de las áreas de los rectángulos y haciendo que el número de rectángulos, n, tiende a infinito.
¿Qué importancia tiene el concepto de la suma de Riemann en el cálculo?
-La suma de Riemann es fundamental en el cálculo porque ofrece una manera intuitiva de entender las integrales definidas como el área bajo una curva, aproximándolas a través de sumas de áreas de rectángulos.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
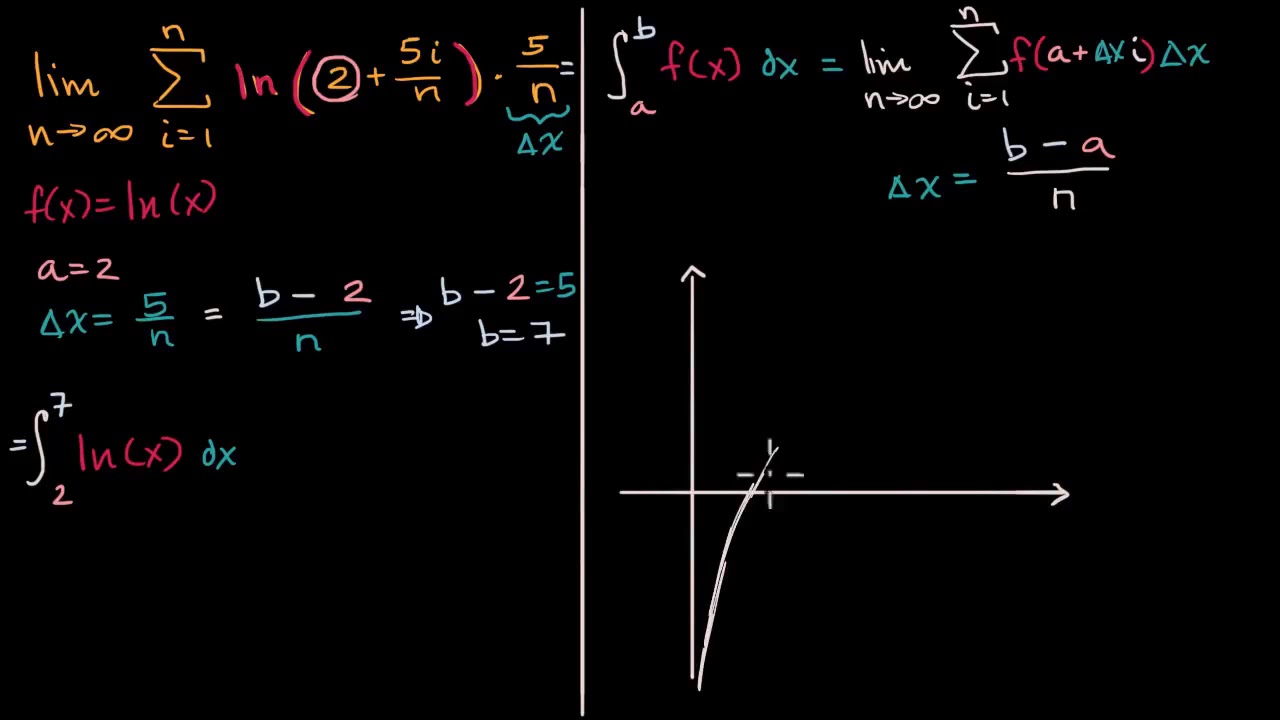
Escribir el límite de una suma de Riemann como una integral definida | Khan Academy en Español

Sumas de Riemann - Ej.1 (Paso a paso | Cuadrática)

Suma de Riemann, paso a paso, MUY FÁCIL

Resolver una Suma de Riemann paso a paso. #MateYisus
Calculo Integral 04: La integral definida. The definite integral.

Introducción al cálculo integral | Khan Academy en Español
5.0 / 5 (0 votes)