Adição e subtração de vetores - Como calcular o vetor resultante
Summary
TLDRThis lesson covers the concepts of vector addition and subtraction, using both the polygon and parallelogram rules. The instructor demonstrates how to calculate vector sums and differences through graphical representations, starting with simple vertical and horizontal vectors, and then more complex angled vectors. The lesson also introduces the Pythagorean theorem for right-angle triangles and a formula for calculating vector sums and differences when vectors form an arbitrary angle. Practical examples involving forces and real-world applications are provided, ensuring that learners can grasp the methodology effectively.
Takeaways
- 📐 The lesson covers the addition and subtraction of vector quantities, focusing on rules like the polygon and parallelogram methods.
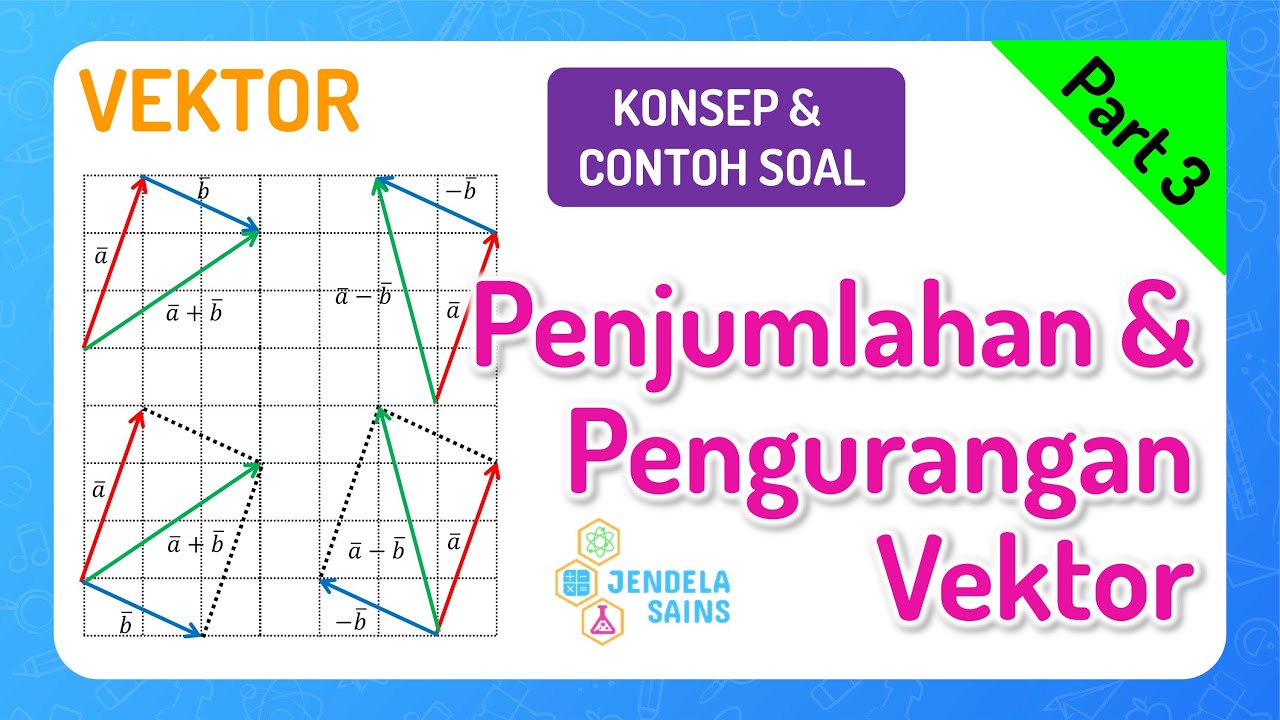
- 📊 To calculate the sum of vectors, the 'polygon rule' is applied by drawing the vectors consecutively and connecting the origin to the endpoint.
- ➡️ Vector addition example: Three vectors A, B, and C are drawn, and the resulting vector S is the sum of A + B + C.
- 📏 Vector subtraction is achieved by reversing the direction of one vector and then applying the same rules as addition.
- 📉 Each small square in the diagrams represents a distance of 1 meter, making it possible to calculate both the direction and magnitude of vectors.
- 📐 Using the Pythagorean theorem is crucial when working with right-angled triangles formed by vectors to calculate the magnitude of the resultant vector.
- ✖️ For subtraction, the procedure is similar to addition but with the second vector reversed in direction.
- 📏 In cases where vectors form an angle (not a right triangle), the general vector formula involves cosine of the angle between them.
- 🔄 The 'parallelogram rule' allows calculating the resultant vector by constructing parallel lines and drawing the diagonal as the result.
- 🔢 Example of vector force calculation: When forces are represented as vectors, the formula involving cosine is used to compute the magnitude of the resultant force.
Q & A
What is the primary topic of the lesson?
-The lesson focuses on vectors, specifically the addition and subtraction of vector quantities using methods like the polygon rule and the parallelogram rule.
What is the first step in performing vector addition using the polygon rule?
-The first step is to draw the first vector (A) and, once that is completed, to draw the second vector (B) starting from the endpoint of the first vector.
How is the resultant vector defined in vector addition?
-The resultant vector (S) in vector addition is the vector that starts from the origin of the first vector and ends at the endpoint of the last vector in the sequence.
How is the magnitude of the resultant vector calculated when adding vectors?
-The magnitude of the resultant vector can be calculated by summing the magnitudes of the individual vectors, assuming they are in the same direction. In other cases, methods like the Pythagorean theorem or vector addition formulas may be used.
What happens to the direction of a vector when subtracting one vector from another?
-When subtracting a vector, the direction of the subtracted vector is reversed. This means it has the same magnitude as the original vector but points in the opposite direction.
How do you calculate the magnitude of the difference between two vectors?
-To calculate the magnitude of the difference between two vectors, you subtract the magnitude of one vector from the other if they are aligned. If they form an angle, you may need to apply the Pythagorean theorem or vector subtraction formulas.
In the lesson, what mathematical rule is applied when vectors form a right triangle?
-The Pythagorean theorem is applied when vectors form a right triangle to calculate the magnitude of the resultant vector (hypotenuse).
What is the parallelogram rule for vector addition?
-In the parallelogram rule, two vectors are drawn from the same origin. Then, parallel lines are drawn from the endpoints of each vector to form a parallelogram. The resultant vector is the diagonal of the parallelogram starting from the common origin.
How do you calculate the magnitude of the resultant vector when the vectors form an angle?
-When vectors form an angle, the magnitude of the resultant vector can be calculated using the formula: R² = A² + B² + 2AB * cos(θ), where θ is the angle between the vectors.
What formula is used when subtracting vectors that form an angle?
-When subtracting vectors that form an angle, the formula used is: R² = A² + B² - 2AB * cos(θ), where θ is the angle between the vectors.
In the example given, how is the resultant force calculated when two forces of 7 N and 8 N form an angle of 60°?
-The resultant force is calculated using the formula R² = A² + B² + 2AB * cos(θ). For forces of 7 N and 8 N with a 60° angle, the formula becomes: R² = 7² + 8² + 2(7)(8) * cos(60°), leading to a resultant force of 13 N.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Operasi Vektor Secara Analitik dan Geometri (Vektor Bagian 3) Matematika Peminatan Kelas 10
Vektor Matematika Kelas 10 • Part 3: Penjumlahan & Pengurangan Vektor

Konsep Vektor Fisika [LENGKAP] - Part 1 : Vektor Fisika Kelas 10

Vektor 1

Vektor (part 5) - Penjumlahan Vektor Metode Jajargenjang

Grandezas vetoriais x escalares - VETORES - Aula 1 - Prof. Marcelo Boaro
5.0 / 5 (0 votes)
