03. Cómo describir una variable numérica | Curso de SPSS
Summary
TLDRThis script discusses key statistical measures for summarizing numerical data. It covers measures of central tendency (mean, median, mode), dispersion (standard deviation, variance, and standard error), position (percentiles, quartiles, deciles), and shape (skewness, kurtosis). The script uses examples like age, weight, and height to explain these concepts, highlighting how they help understand data distribution and variability.
Takeaways
- 📊 Describing a numerical variable involves summarizing it through various measures: central tendency, dispersion, position, and shape.
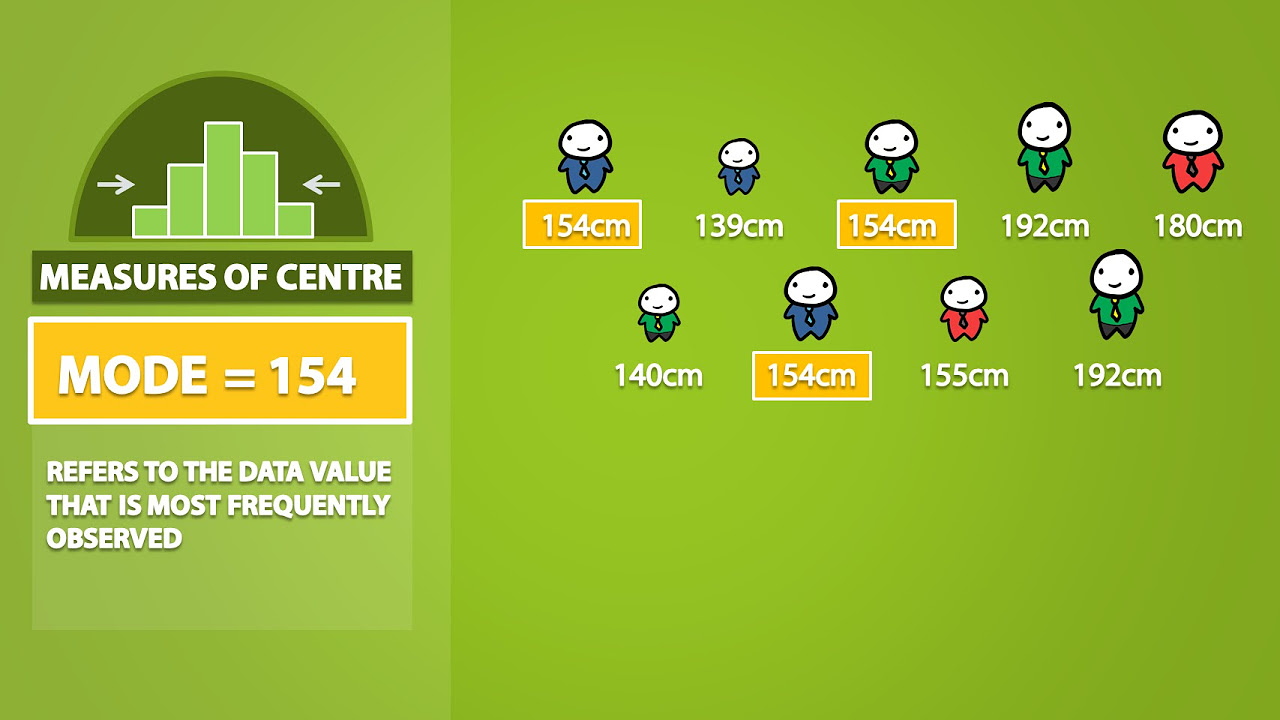
- 🔢 Central tendency measures include the mean (average), median (middle value), and mode (most frequent value). A normal distribution has the same mean, median, and mode.
- 🧮 Mean is calculated by summing all data points and dividing by their count. Median is the middle value when data is ordered. Mode is the most repeated value.
- 📉 Dispersion measures like standard deviation, variance, and standard error indicate how spread out the data is relative to the mean.
- 📏 Standard deviation shows data spread relative to the mean, variance is the square of standard deviation, and standard error is the standard deviation of the mean.
- 📋 Position measures such as percentiles, quartiles, and deciles divide data into 100, 4, and 10 equal parts, respectively, to understand data distribution.
- 📊 Quartiles (Q1, Q2, Q3) and percentiles (e.g., P23) are specific types of position measures that provide insights into data distribution.
- 📈 Shape measures like skewness and kurtosis are quantified by the skewness coefficient and kurtosis coefficient, indicating the symmetry and peakedness of the data distribution.
- 🔄 Positive skewness indicates a right tail, negative skewness indicates a left tail, and zero skewness suggests a symmetrical distribution.
- 📊 Kurtosis measures the 'tailedness' of the distribution; positive kurtosis indicates a leptokurtic distribution, negative indicates a platykurtic distribution, and zero suggests a mesokurtic distribution.
Q & A
What are the main types of measures used to summarize numerical variables?
-The main types of measures used to summarize numerical variables are measures of central tendency, measures of dispersion, measures of position, and measures of shape.
What are the three most common measures of central tendency?
-The three most common measures of central tendency are the mean (average), median, and mode.
How is the mean calculated and what is an example from the script?
-The mean is calculated by summing all the data points and dividing by the number of data points. An example from the script is the mean age of a group of people, which is 31 years.
What is the median and how does it relate to the data set's order?
-The median is the value that lies in the middle of a data set when it is ordered from least to greatest. In the script, the median age is 29 years.
What is the mode and what does it indicate about the data?
-The mode is the value that appears most frequently in a data set. It indicates the most common value among the data points. In the script, the mode of age is 27 years.
If the mean, median, and mode of a distribution are the same, what does this suggest about the distribution?
-If the mean, median, and mode are the same, it suggests that the distribution is normal.
What are the primary measures of dispersion and how do they differ?
-The primary measures of dispersion are the standard deviation, variance, and the standard error. The standard deviation measures how spread out the data is from the mean. Variance is the square of the standard deviation and is used in most statistical procedures. The standard error is a measure of how spread out the sample means are from the population mean.
What is the standard error of the mean and why is it important?
-The standard error of the mean is a measure of how much variability or 'spread' exists in the sample means over all possible samples. It is important because it provides an estimate of how close the sample mean is likely to be to the true population mean.
What are measures of position and how are they calculated?
-Measures of position include percentiles, quartiles, and deciles. They are calculated by dividing the data set into 100, 4, and 10 equal parts respectively, and identifying the values that correspond to these divisions.
What is the significance of the 23rd percentile mentioned in the script?
-The 23rd percentile mentioned in the script is an example of a measure of position that divides the data set into 100 parts and identifies the value that corresponds to the 23rd part.
What are measures of shape and how are they used to describe a distribution?
-Measures of shape include skewness and kurtosis. They are used to describe the shape of a distribution's tails. Skewness measures the asymmetry of the distribution, while kurtosis measures whether the distribution is peaked or flat relative to a normal distribution.
What does a positive skewness coefficient indicate about a distribution?
-A positive skewness coefficient indicates that the distribution has a longer tail on the right side, meaning there are more values on the higher end of the distribution.
What does a positive kurtosis value suggest about the distribution?
-A positive kurtosis value suggests that the distribution is leptokurtic, meaning it is more concentrated around the mean and has heavier tails compared to a normal distribution.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Statistics For Data Science | Data Science Tutorial | Simplilearn

Mathematics in the Modern World - Data Management (Part 1)

Statistika Deskriptif Ukuran Pemusatan dan Penyebaran Data | Zulfanita Dien Rizqiana, S.Stat., M.Si.
Mode, Median, Mean, Range, and Standard Deviation (1.3)
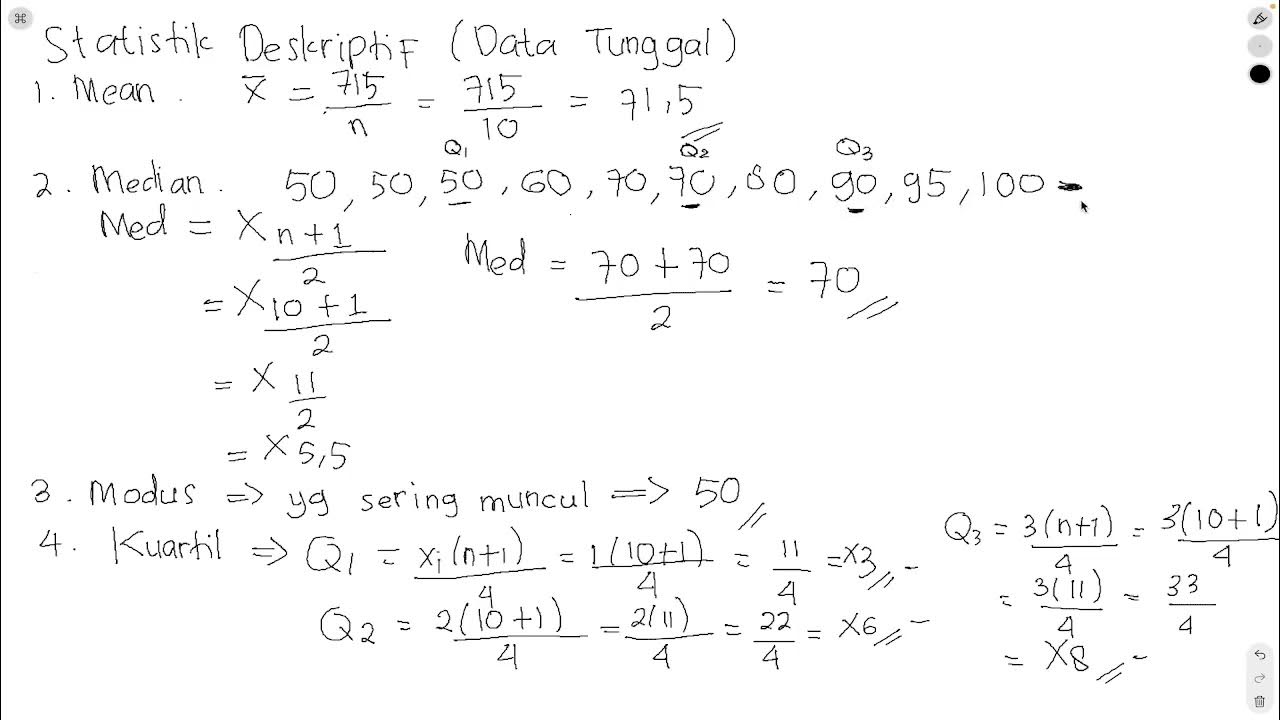
STATISTIK DESKRIPTIF (MEAN, MEDIAN, MODE, KUARTIL, VARIAN, STANDAR DEVIASI) UNTUK DATA TUNGGAL

Descriptive Statistics vs Inferential Statistics
5.0 / 5 (0 votes)
