Markov Chains and Text Generation

Summary

This video delves into Markov chains, illustrating their concept through a car's functional and broken states. It explains how to model states and transition probabilities, representing them as a table or matrix. The video progresses to demonstrate generating text using Markov chains, showing how to create states for each word and calculate transition probabilities. It uses 'the quick brown fox jumps over the lazy dog' as a simple example and then scales up with a chain trained on 5,000 Wikipedia articles. The video also touches on advanced text generation using n-grams and concludes with a unique application of Markov chains in generating novel, human-like pen strokes.

Takeaways

• 🔄 Markov chains are used to model transitions between states, with each state representing a condition or an event.
• 🚗 The script uses the example of a car's condition (working or broken) to explain how Markov chains can model real-life situations.
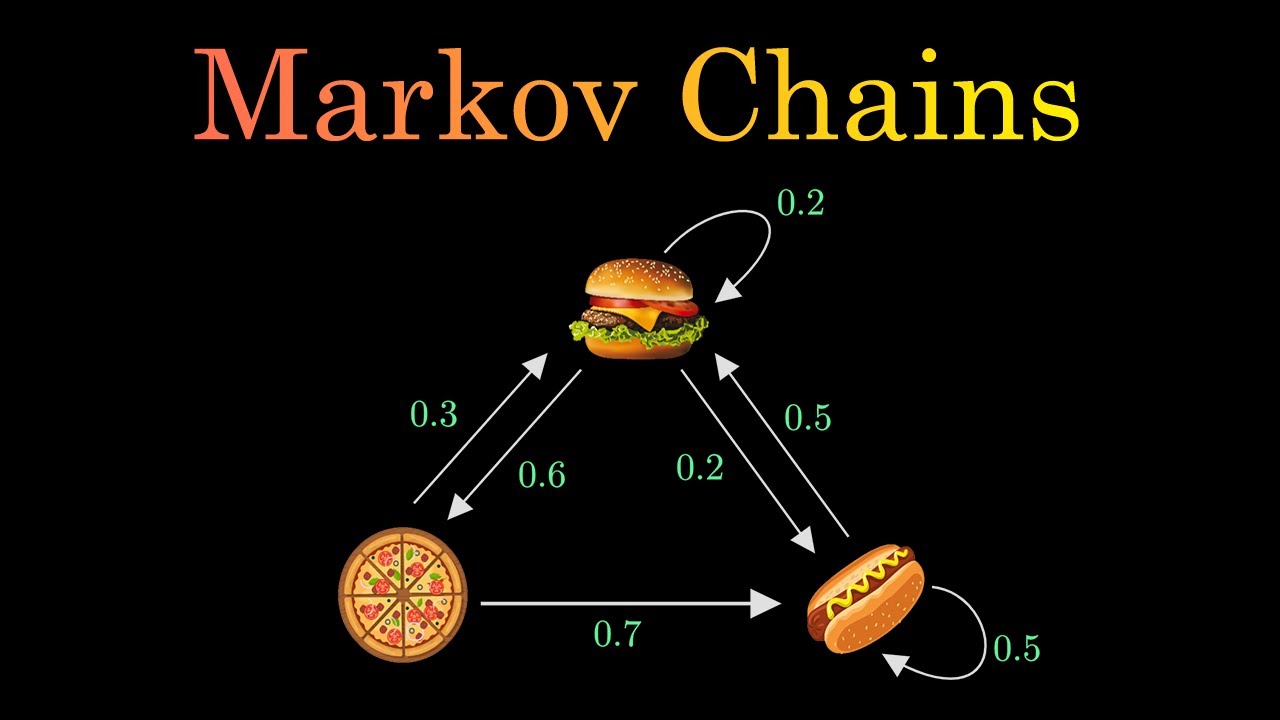
• 📊 Transition probabilities in a Markov chain can be represented as a table or matrix, showing the likelihood of moving from one state to another.
• 📈 Data collection and analysis are crucial for determining the probabilities within a Markov chain, such as observing the frequency of car breakdowns over time.
• 📝 Markov chains can be applied to text generation by treating each word as a state and modeling the likelihood of subsequent words.
• 📖 The script demonstrates how to create a Markov chain from a simple sentence, showing the transition probabilities between words.
• 🌐 Training a Markov chain on a large dataset, like Wikipedia articles, can generate more complex and realistic text predictions.
• 🔡 Text generation using Markov chains involves selecting the next word based on the current word's state, using probabilities to bias the choice.
• 🔗 Markov chains can be extended to consider n-grams (multiple words) instead of single words, improving the coherence of generated text.
• 🎨 Beyond text, Markov chains can model and generate other types of sequences, such as drawing strokes, creating unique and human-like patterns.

Q & A

What is a Markov chain?

A Markov chain is a mathematical system that models a sequence of possible events where the probability of each event depends only on the state attained in the previous event.

How are states and transitions represented in a Markov chain?

In a Markov chain, states are represented by nodes or circles, and transitions between states are represented by arrows pointing from one state to another, indicating the likelihood of moving from one state to the next.

What is the significance of the car example used in the script?

The car example illustrates a simple Markov chain with two states: the car working or the car broken. It demonstrates how probabilities are used to model the likelihood of transitioning between these states.

How can the data from a Markov chain be represented?

Data from a Markov chain can be represented as a table or a matrix, where rows represent the current state and columns represent the next state, with the values indicating the probability of transitioning from one state to another.

What is the process for converting raw data into probabilities in a Markov chain?

To convert raw data into probabilities, the total occurrences for each state are calculated and then each occurrence count is divided by the total for that state, resulting in a probability for each transition.

How does the Markov chain model handle text generation?

In text generation, each word is treated as a state, and the transitions are the probabilities of one word following another. This is used to predict and generate the next word in a sequence based on the previous word or words.

What is the significance of the 'the' word in the Markov chain text generation example?

The word 'the' is significant because it appears multiple times in the example sentence, allowing for different transition probabilities to be observed and modeled, unlike other words that appear only once.

How can the randomness in text generated by a Markov chain be controlled?

The randomness in text generated by a Markov chain is controlled by biasing the selection of the next word based on the probabilities defined by the chain, ensuring that some words are more likely to follow others.

What is the limitation of a Markov chain when generating text based on single-word states?

The limitation of a Markov chain when generating text based on single-word states is that the generated text can diverge in meaning very quickly, as each word only depends on the immediately preceding word.

How can the coherence of generated text be improved in a Markov chain model?

The coherence of generated text can be improved by making each word depend on the last two or three words instead of just the last word, creating a more complex state that considers word pairs or triplets.

What other applications of Markov chains are mentioned in the script?

Apart from text generation, the script mentions using Markov chains to model and generate pen strokes for drawing, which can emulate human-like scribbles and create new, never-before-seen images.

Outlines

00:00

🚗 Introduction to Markov Chains

The paragraph introduces the concept of Markov chains using a car's functional state as an example. It explains how Markov chains can model the probability of transitioning between different states, such as a car being either functional or broken. The speaker outlines the probabilities of moving from one state to another, like the car remaining functional or breaking down, and the likelihood of fixing a broken car. The concept is visualized through a simple diagram and a transition probability table, which is essentially a matrix representing the probabilities of state transitions. The paragraph also touches on how to gather data to create such a table and how to convert raw data counts into probabilities by dividing the number of occurrences by the total number of observations for each starting state.

05:00

📝 Markov Chains in Text Generation

This paragraph delves into applying Markov chains to text generation. It uses the sentence 'The quick brown fox jumps over the lazy dog' to illustrate how each word can be considered a state with transitions to subsequent words based on their appearance in the sentence. The speaker discusses creating a Markov chain model by determining the probabilities of moving from one word state to another, such as the word 'the' leading to 'quick' or 'lazy' with a 50% chance each. The concept is expanded by training a Markov chain on a larger dataset of 5,000 Wikipedia articles to better understand the probabilities of word sequences in English. The paragraph concludes with an explanation of how to generate random text using a Markov chain by selecting the next word based on the current word's state, using probabilities to bias the selection.

10:01

🎨 Advanced Text Generation and Creative Applications

The final paragraph discusses advanced techniques for text generation using Markov chains, such as considering the last two or three words to generate the next word, which helps maintain context and coherence in the generated text. The speaker also shares a creative application of Markov chains in generating artwork based on recorded pen strokes. By training a Markov chain on segments of mouse movement data, the program can generate new drawings that resemble human scribbles. This demonstrates the versatility of Markov chains beyond text generation, showcasing their potential in mimicking complex patterns and behaviors.

Keywords

💡Markov Chain

A Markov Chain is a stochastic model that describes a sequence of possible events where the probability of each event depends only on the state attained in the previous event. In the video, the concept is introduced through the analogy of a car's functional state, illustrating how it can transition from working to broken and vice versa based on certain probabilities. The video also demonstrates how Markov Chains can be used to generate text, with each word's state influencing the next word in a sequence.

💡State

In the context of the video, 'state' refers to a condition or status within the Markov Chain model, such as the car being in a 'working' or 'broken' state. Each state represents a point in the sequence where a transition to another state can occur. The video uses the car example to explain states and further applies this concept to text generation, where each word represents a state.

💡Transition

A 'transition' in a Markov Chain is the movement from one state to another. The video script describes how transitions are quantified by probabilities, such as the likelihood of a car breaking down or being fixed. This concept is central to understanding how Markov Chains model sequences, as each transition is governed by a set probability.

💡Probability

Probability, as discussed in the video, is a measure of the likelihood that a particular event will occur. It is a fundamental aspect of Markov Chains, where the probability of transitioning from one state to another is crucial. The video provides examples such as the 1% chance of a car breaking down or the 90% chance of fixing a broken car, emphasizing how probabilities dictate the behavior of a Markov Chain.

💡Text Generation

Text generation is a practical application of Markov Chains demonstrated in the video. It involves creating a sequence of words (states) where each word is chosen based on the probability of it following the previous word. The video script uses the sentence 'the quick brown fox jumps over the lazy dog' to illustrate how a Markov Chain can be constructed from text, with each word leading to the next with certain probabilities.

💡Matrix Representation

The video mentions representing a Markov Chain as a table or matrix, where rows and columns represent states and transitions between states, respectively. This method provides a structured way to visualize and calculate probabilities within the model. The matrix is a practical tool for encoding the behavior of the Markov Chain.

💡Data Gathering

Data gathering is referenced in the video as a method to determine the probabilities within a Markov Chain. The speaker describes a hypothetical scenario of recording car states over a period to populate a table with raw counts, which are then converted into probabilities. This process is essential for training a Markov Chain model with real-world data.

💡Training

Training, in the context of the video, refers to the process of developing a Markov Chain model using a dataset. The video describes how one might train a Markov Chain on a set of Wikipedia articles to understand the likelihood of word sequences in the English language. This training process allows the model to generate new text that resembles natural language.

💡Random Block of Text

A 'random block of text' is a sequence of words generated by a Markov Chain, as discussed in the video. The generation process involves selecting each subsequent word based on the current state (word) and the associated probabilities. The video explains how this process can be biased towards certain words to create a coherent, albeit random, block of text.

💡Biased Randomness

Biased randomness is a concept introduced in the video to describe the generation of text by a Markov Chain. It refers to the method of selecting the next word in a sequence not by pure chance but according to the probabilities defined by the model. This ensures that the generated text follows natural language patterns, even though it is random.

💡Pen Strokes

Pen strokes are used in the video to demonstrate a non-text application of Markov Chains. The speaker trained a Markov Chain on recorded pen movements to generate new drawings that emulate human scribbles. This example shows how Markov Chains can model sequences in various forms, not just text.

Highlights

Introduction to Markov chains and their applications in text generation.

Explanation of a Markov chain using a simple car maintenance example.

Visual representation of a Markov chain with states and transitions.

Conversion of a Markov chain diagram into a table format for easier understanding.

Gathering data to determine transition probabilities in a Markov chain.

Calculating probabilities from raw data counts to understand state transitions.

Application of Markov chains to text generation using a simple sentence.

Creating states for each word in a sentence to model text with a Markov chain.

Defining transition probabilities between words in a Markov chain model.

Building a larger Markov chain using 5,000 Wikipedia articles for text generation.

Demonstration of predicting the next word in text using a Markov chain.

Explaining the process of generating random text using a Markov chain.

Advantage of using Markov chains for predicting user input in mobile keyboards.

Technique for generating text where each word depends on the last two or three words for better context.

Generating random blocks of text with a Markov chain by picking words in a biased random manner.

Using Markov chains to generate pen strokes that emulate human-like drawings.

Conclusion and summary of the video's exploration of Markov chains.

Transcripts

pictures can also refer to translation

to machine code for correctly rounded

when converted to Islam in material okay

so that probably didn't make a whole lot

of sense but that's because a human

didn't write that sentence a machine did

using something called a Markoff chain

today I'm going to be talking about

markof chains and some of their

applications including things like text

generation like you just saw so I want

to start off by talking about a really

simple example in real life where a

Markoff chain might arise imagine the

only thing I care about is whether or

not my car works so there's just two

states the world can be in either my car

is functional you know I can use it to

drive to work whatever or my car is

broken you know it's useless sitting in

my driveway or whatever and I just

cannot cannot get anywhere with my car

so now I want to start thinking about

the probability you know the likelihood

that I will go between these two

situations so let's say most of the time

if I wake up and my car works in the

morning it's probably going to be

working at night still when I go to bed

you know there's a small chance I'll

have a breakdown in the middle of the

day let's call that let's say a 1%

chance so there's a 1% chance I'll go

from the car Works state to the car

broken State now let's suppose that once

my car is broken I really want it fixed

so if I wake up on a given day and my

car is broken in the morning there's a

90% chance I'll have it fixed by the end

of the day so we can represent that this

way and now there's a final piece of

this picture which I don't already have

drawn here which is you know 99% of the

time my car works it will stay working

and 10% of the time my car is broken

it'll stay broken so I can represent

these just with arrows pointing into the

the same state that they come out of so

this is just an example of a Markov

chain basically what we have is we have

a bunch of States you know in this case

just two different states either my car

is functional or it's broken and we have

transitions between those States you

know the likelihood that you'll go from

one state to another given State and

finally one last thing we can do is we

can represent this Markoff chain instead

of by using like these arrows and these

circles we can also represent it as a

table and in this case I've chosen to

make the the rows the state you're

coming from and the columns the state

you're going to so if uh currently my

car is broken and I want to know the

odds that uh it will stay broken I would

look at the bottom right uh corner of

this table in this case so this is just

another way I can write down a Markoff

chain I can just write it down as a

table or as a matrix so you might be

wondering how could I actually gather

this data you know how would I find out

that 99% of the time my car Works it'll

keep working and 90% of the time my car

is broken I'll get it fixed you know how

do I figure out these probabilities you

know in a real life situation and one

way to do that is to just gather a lot

of data so suppose I spent you know a

little over 2 years just every day I

just in the morning note whether my car

works and at night I note whether my car

works and so I could fill in this table

and so the idea is let's say I started

the day and my car was broken I ended

the day and my car was working I would

just add one to that cell in the table

um and I might get something that looks

a little bit like this so this this is

just the kind of thing I would get if I

just gathered a bunch of data so now

we're left with the task of turning this

table of data into a table of

probabilities you know before we had a

table with you know 90% 99% 1% and now

we just have a table with a bunch of

numbers so how do we get from this to

that so really let's think about what a

probability actually is if I start the

day with a working car and I want to

know the probability that at the end of

the day my car will be broken I want to

know you know maybe nine times out of 10

it'll be broken or you know 50 times out

of 100 it'll be broken or you know

whatever whatever the measure I'm doing

it out of something so if my car is

broken 8 times uh when it was working in

the morning you know eight times out of

what is basically what I'm wondering you

know if I took if I took 800 samples

where I started the day with my car

working and there were only eight where

I was broken at the end of the day it

there's an eight out of 800 chance that

my car will break down on a given day so

to turn this into an actual formal

procedure I'm just going to add another

column to this table which is the total

number uh the total sum of that entire

row so for the first row uh days

starting with my car working you can see

that there's a total of 800 days where I

started my day and my car was working

and there were a total of 10 days when I

started my day and my car wasn't working

and what this allows me to do is in the

first row I can just divide all those

things by 800 and in the second row I

can divide those things by 10 and so now

in the first row I can see that if I

wake up with my car working 792 out of

800 times I will go to bed with my car

working as well so really this just

turns uh turns our you know our raw

counts our raw you know number of days

this happened it turns them into

probabilities and if we express them as

percentages uh we get something like

this which is actually what we had

before um if you remember what did you

know the original example I presented

you before so how do we apply this idea

of states and transition probabilities

to something like the example I showed

at the beginning of the video where I

used a Markov chain to generate a bunch

of text what we're really looking for is

a way to represent a piece of text as a

bunch of states and transitions between

states and so I'm going to show how to

do this and I'm just going to use a toy

sentence the quick brown fox jumps over

the lazy dog because it's pretty simple

to work with this you know this small

amount of text the first thing I'm going

to do is create a state for each word

that appears in this sentence so I have

a state for quick a state for brown a

state forthe and the way I'm going to

Define a state is as you read the

sentence whatever word you're currently

reading is the state that you're in so

if I go through and read this I start

out in theth state I go to quick I go to

Brown I go to Fox I go to jumps I go to

over back to the th State then finally I

go to lazy and then dog the next step to

building this Markov chain is thinking

about the probabilities of going between

each state so let's start with theth

state becausethe is the only word that

appears in this sentence twice the first

time we saw the' we went to quick and

the second time we saw the we went to

Lazy right afterwards so there's

actually a 50% probability in the state

' that we go to Quick next and a 50%

probability that we go from the state

the to the state lazy next now if we

look at any other word let's say we do

fox fox only appears one time in the

sentence and jumps happens right after

it so there's a 100% probability that

the next thing after the fox state will

be the jump State there's just nothing

else that we can go to from the fox

State and this is true for every word

except for the wordthe becausethe is the

only word that even happens multiple

times in this sentence so if we wanted

to turn this into a Markov chain we

would get something like this where the

wordthe branches off into quick and lazy

with a 50% chance in each Direction and

every other word just goes into the next

word with 100% probability because

there's nothing else that ever comes

after that word so the point of this

example is to just show you how we could

build the markof chain using text you

know we represent each word as a a state

we represent the transitions as you know

the likelihood that a given word will

come after the word before it and this

sentence you know because it's just you

know a few words doesn't give us that

good an idea of how the Eng how the

English language is structured you know

it doesn't tell us much about which

words come after other words although it

does show us that the word the is pretty

common um so what I've done to get a

better example of a bigger Markoff chain

is I've taken about 5,000 Wikipedia

articles and I've trained a markof chain

on that you generated a big markof chain

for all the words that appear in there

you know hundreds of thousands of words

and I'm just going to show you the state

for the word the' so here we have uh you

know I've simplified it I have this

thing other stuff in the corner

basically for things I didn't want to

fit in so this is just the most common

transitions out of the wordthe we see

first is the most likely word to come

after the wordthe right after it is

United probably from the United States

then same most Etc and what this shows

is you know if I if I'm just reading

text and all I know all I'm told is the

last word I saw was the word the' I can

predict you know first same most City

are all pretty likely words to happen

and you know I know what's likely to

come next so the Markov chain is a model

basically of the probabilities of you

know certain words following other words

when we use it in terms of text so we've

already done a great deal and this is

actually already a pretty useful model

to have say if you're making a keyboard

for iOS or another mobile operating

system and you want it to be able to

predict what the next word the user is

going to type is uh this is actually a

Fairly reliable system to do that now

it's not necessarily the best system

because it just depends on the last word

that they typed but it does take some

context into account and it could

actually do a pretty decent job uh of

suggesting which word to type so now I

still have to explain how we can use

this to actually generate a random block

of text and basically uh I'm just going

to explain how we generate the next word

in a block of text because if you can

generate the next word then you can keep

generating words and you get a large

string of text in the end so let's say

we've just generated the word the in our

random block of text well we're going to

pick the next word we generate randomly

because it's random but we're going to

do it in a biased way and you know we're

going to bias the next word in a way

where first is more likely than end and

you know United is more likely than

other and actually we're going to bias

it exactly so even if we're picking the

next word randomly we're going to be

picking it randomly in such a way that

first has a 1.33% chance of happening

same has a 0 90% chance of happening

Etc so we're picking randomly but we're

doing it in a biased fashion and we're

biasing it the same way our Markov chain

says we should bias it you know if it

says first happens more than city after

the wordthe then we're going to pick

randomly in that biased way we're going

to do it the way the markof chain says

to do it uh you can think of maybe uh

this is kind of like flipping a biased

coin where instead of being 50% heads

50% taals it's 75% heads 25% taals it's

still random what happens but one CH one

thing is still more likely than the

other thing this is kind of like that

one last thing I'll mention is that this

technique of generating random blocks of

text uh the way it works is each word

only depends on the word that comes

before it and so the thing diverges in

meaning extremely fast you know a couple

words down the line there's just no

connection to what was said before and

one way to fix this problem is to make

each word you generate depend not on the

last word but on the last two words or

the last three words and you can

actually set that up in a way that's

similar to this but instead of you know

all the words coming off ofth you might

have all of the words that come after

the phrase like the the same or the most

you know something like that so you'd

have pairs of words in a state instead

of just a word in a state and that's

actually what I did to generate the

block of text you saw at the beginning

of the video but that's not really

essential to the idea of a Markov chain

uh it's just the same thing but with

more words in a given state so now I

want to conclude the video by just

showing one other cool thing you can do

with Markov chains that has nothing to

do with text generation I made a program

where I could draw tons of stuff and it

would record the pen Strokes that I made

so it would record how I uh move my

finger you know over a brief interval or

my mouse and uh you know the direction

in which I moved it basically and then I

trained a Markoff chain basically based

on uh these pen stroke so I trained to

markof chain on small segments of um of

of where I moved my mouse basically and

so each state is basically you know what

direction is the is the mouse you know

sliding at that time and how fast is it

sliding stuff like that and I used that

to generate new images that had never

been drawn before and what's remarkable

about these images is even though

they're not letters or numbers or

anything uh truly meaningful they

actually do look like something a human

could draw there's curls and squiggles

it's not just a purely random drawing it

actually emulates the pen Strokes that a

human might make while scribbling on uh

on their mouse or on a touch screen so I

thought that was pretty interesting and

just a cool little other uh thing you

could do with a Markoff chain that

doesn't really have to do with text

Generation Um so I hope you enjoyed this

video and I hope you learned something

from it thanks for watching and goodbye