MATERI KINEMATIK kelas 11 bag 8 GERAK MELINGKAR BERATURAN GMB K Merdeka
Summary
TLDRThis educational script covers the fundamental concepts of circular motion, specifically uniform circular motion (GMB). Key topics include period and frequency, linear and angular displacement, and the relationship between linear velocity (V) and angular velocity (Omega). The script explains how to convert angular velocity from rotations per minute (RPM) to radians per second, and it introduces the formula for centripetal acceleration (A_s = V²/r or A_s = Omega² * R). The lesson is designed to help students understand and apply these principles to solve problems related to circular motion.
Takeaways
- 🔄 Circular motion is a type of movement where the path is circular, such as in the case of a spinning wheel or a bicycle.
- ⏱️ The period (T) and frequency (f) are fundamental concepts in circular motion, where T represents the duration of one complete cycle and f is the number of cycles per second.
- 🔄 Linear and angular displacement are key in circular motion, with angular displacement being the change in angle as the object moves in a circle.
- 📏 The relationship between linear displacement (Δx) and angular displacement (Δθ) is given by the formula Δx = Δθ * r, where r is the radius of the circle.
- 🚀 The linear velocity (V) in circular motion is calculated by the formula V = ω * r, where ω is the angular velocity and r is the radius.
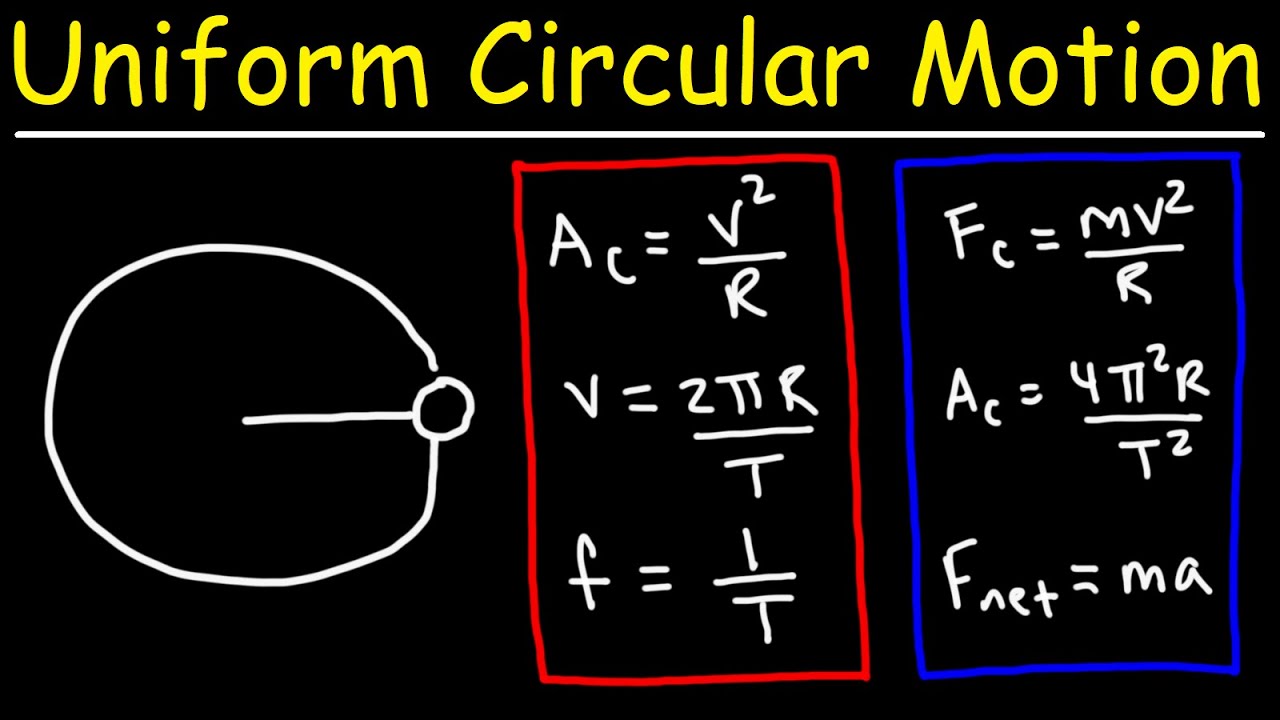
- 🌀 Centripetal acceleration (a) is always directed towards the center of the circle and is calculated by the formula a = v²/r or a = ω² * r.
- 🔄 Conversion between angular velocity (ω) and revolutions per minute (RPM) is essential, where ω = 2π * (RPM/60).
- 🔢 To convert degrees to radians for calculations in circular motion, use the conversion 180° = π radians.
- 📐 The circumference of a circle, which is relevant for linear displacement in circular motion, is given by the formula C = π * d, where d is the diameter.
- 🎯 Understanding and applying these principles of circular motion is crucial for solving related physics problems and understanding real-world applications like motion in engines and rotational mechanics.
Q & A
What is the definition of circular motion as described in the script?
-Circular motion is defined as a movement where the path of the object is in the shape of a circle.
What are the two types of circular motion mentioned in the script?
-The two types of circular motion mentioned are GMB (Uniform Circular Motion) and GMBB (Variable Circular Motion).
What does the acronym 'GMB' stand for in the context of the script?
-GMB stands for 'Gerak Melingkar Beraturan', which translates to 'Uniform Circular Motion'.
What are the two main quantities discussed in relation to circular motion in the script?
-The two main quantities discussed are 'period' and 'frequency', which are represented by the symbols 't' and 'f' respectively.
What is the formula for the period 't' in terms of 'n' as described in the script?
-The formula for the period 't' in terms of 'n' is given by 't = n/f', where 'n' is the number of rotations and 'f' is the frequency.
How is linear displacement related to angular displacement in circular motion according to the script?
-Linear displacement is related to angular displacement through the formula Δx = Δθ * r, where Δθ is the angular displacement, and 'r' is the radius of the circle.
What is the formula for converting angular velocity from revolutions per minute (RPM) to radians per second?
-To convert angular velocity from RPM to radians per second, the formula used is (RPM * 2π) / 60.
What is the relationship between linear velocity 'v' and angular velocity 'ω' as explained in the script?
-The relationship between linear velocity 'v' and angular velocity 'ω' is given by the formula v = ω * r, where 'r' is the radius of the circular path.
What is the formula for centripetal acceleration 'a' in terms of linear velocity 'v' and radius 'r'?
-The formula for centripetal acceleration 'a' in terms of linear velocity 'v' and radius 'r' is a = v² / r.
How is angular velocity 'ω' related to frequency 'f' in the context of circular motion?
-Angular velocity 'ω' is related to frequency 'f' through the formula ω = 2π * f.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Gerak Melingkar • Part 1: Sudut Radian & Gerak Melingkar Beraturan (GMB)

CBSE Class 9 || Physics || Motion || Animation || in English @digitalguruji3147

FISIKA Kelas 10 - Gerak Melingkar | GIA Academy
Uniform Circular Motion Formulas and Equations - College Physics

GERAK BENDA DALAM BIDANG DATAR DENGAN PERCEPATAN TETAP

Movimento Circular Uniforme
5.0 / 5 (0 votes)
