(LENGKAP) Sudut pusat dan sudut keliling
Summary
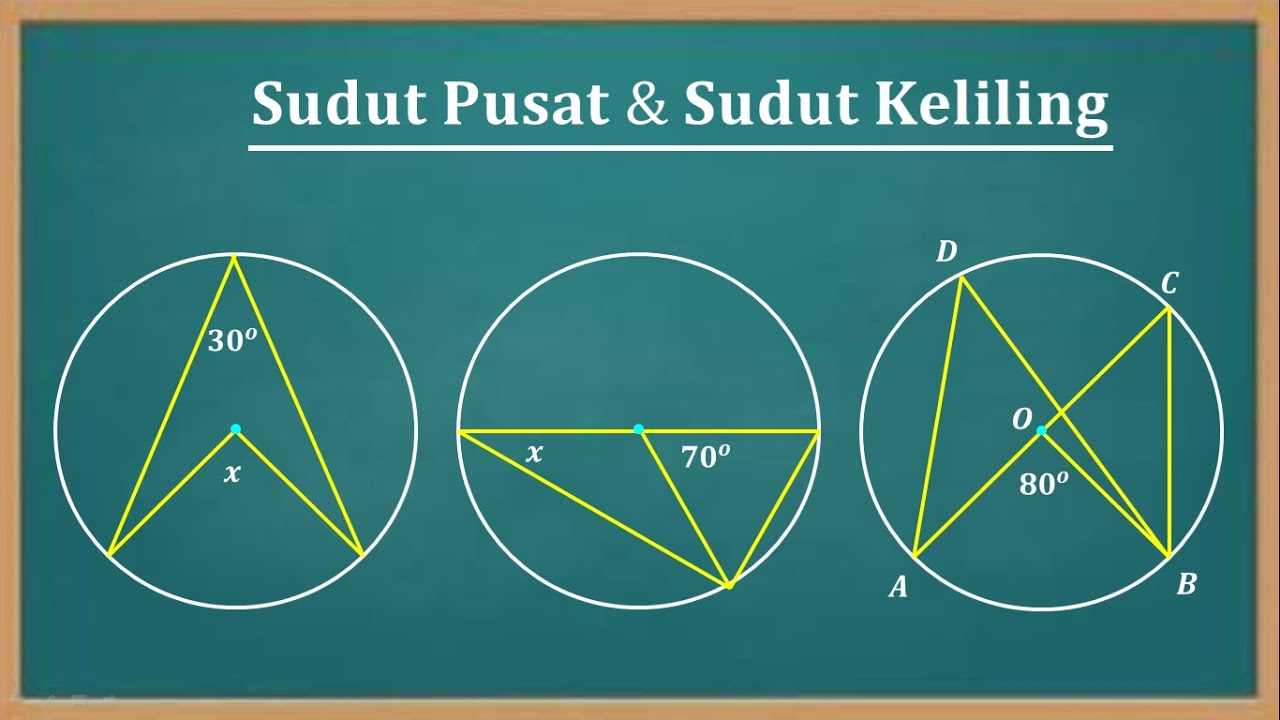
TLDRThis educational video script discusses the concepts of central and circumferential angles in relation to circles. It explains that the central angle is twice the measure of the circumferential angle, and all circumferential angles subtended by the same arc are equal. The script also covers the fact that a circumferential angle subtended by a diameter is always 90 degrees. Several examples are provided to illustrate how to calculate the measures of these angles, making the complex geometry topics accessible and engaging for viewers.
Takeaways
- 📚 The video discusses the concepts of central angles and peripheral angles in relation to circles.
- 🔢 The value of a central angle is equal to twice the value of the peripheral angle, which is a key relationship explained in the video.
- 📐 The video illustrates how to calculate the size of peripheral angles by using the central angle, emphasizing the mathematical relationship between them.
- 📈 It highlights that all peripheral angles that face the same arc have equal measures, which is a crucial property of circles.
- 📉 The video explains that a peripheral angle that faces a diameter is always 90 degrees, a fundamental theorem in circle geometry.
- 📝 The script provides a step-by-step approach to solving problems involving central and peripheral angles, using examples to clarify the concepts.
- 👨🏫 The tutorial includes a variety of examples and exercises to help viewers understand the application of these geometric principles.
- 📊 The video emphasizes the importance of understanding the relationship between the angles and the arcs they subtend in solving circle-related problems.
- ✅ The presenter encourages viewers to practice and apply the concepts learned to ensure a thorough understanding of the material.
- 🌐 The video concludes with a reminder of the significance of these geometric concepts and their applications in solving problems related to circles.
Q & A
What is the relationship between the central angle and the circumferential angle of a circle?
-The central angle is equal to twice the circumferential angle. For example, if the central angle (∠AOB) is 80 degrees, then the circumferential angle (∠ACB) is half of that, which is 40 degrees.
How can you determine the size of a circumferential angle that faces the same arc?
-All circumferential angles that face the same arc are equal in size. For instance, if ∠ABD and ∠ACD both face arc AD, then their sizes are the same.
What is the degree measure of a circumferential angle that faces a diameter?
-A circumferential angle that faces a diameter is always 90 degrees. This is because the diameter subtends a right angle to any point on the circumference of the circle.
How do you calculate the circumferential angle if you know the central angle and the relationship between them?
-If you know the central angle (∠AOD) and it is given that ∠AOD is 40 degrees, you can find the circumferential angle (∠ACD) by dividing the central angle by two, which would be 20 degrees in this case.
What is the significance of the sum of angles in a triangle within the context of this script?
-The sum of angles in a triangle is always 180 degrees. This property is used to find unknown angles when the other two angles are known.
How can you find the measure of an angle if you know the measure of another angle that is supplementary to it?
-If you know the measure of an angle and you need to find a supplementary angle (sums up to 180 degrees), you subtract the known angle from 180 degrees.
What is the relationship between the angles that are inscribed in a semicircle?
-Angles inscribed in a semicircle are right angles (90 degrees). This is a consequence of the Inscribed Angle Theorem.
If you know the measure of two angles that form a straight line with a third angle, how do you find the measure of the third angle?
-If two angles are known to form a straight line with a third angle, the measure of the third angle can be found by subtracting the sum of the known angles from 180 degrees.
How do you determine the measure of an angle that is part of a set of equal circumferential angles around a circle?
-If you have a set of equal circumferential angles around a circle and the sum is known, you divide the total sum by the number of angles to find the measure of each individual angle.
What is the measure of the central angle if three equal circumferential angles sum up to 96 degrees?
-If three equal circumferential angles sum up to 96 degrees, each angle would be one-third of that sum, which is 32 degrees. The central angle would then be twice the measure of one circumferential angle, resulting in 64 degrees.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Materi Lingkaran dan Busur Lingkaran Bab 2 Matematika Umum Kelas 11 SMA Kurikulum Merdeka

Sudut Pusat dan Sudut Keliling Lingkaran | Latihan 2.1 Halaman 57

Lingkaran [Part 2] - Sudut Pusat dan Sudut Keliling
Sudut pusat dan sudut keliling lingkaran

Lingkaran dan Busur Lingkaran | #PekanBuktiKarya

Lingkaran kelas 11 / Video Teorema Lingkaran
5.0 / 5 (0 votes)
