05. Posición y velocidad en 2 dimensiones

Summary

El guion explica cómo calcular la velocidad instantánea de un objeto conociendo su posición en función del tiempo. Se ilustra con ejemplos en dos dimensiones, derivando la función de posición para obtener la velocidad en un momento específico. Además, se destaca la diferencia entre velocidad (vector) y rapidez (magnitud del vector de velocidad), y se menciona la importancia de las unidades de medida en el cálculo final. El vídeo agradece el apoyo de suscriptores y patrocinadores.

Takeaways

• 📐 Para calcular la velocidad instantánea de un objeto, se necesita conocer su posición en función del tiempo.
• 🕒 La posición del objeto se puede representar como un vector en el plano cartesiano para cada instante del tiempo.
• 📉 La trayectoria del objeto se obtiene sustituyendo valores de tiempo en la función de posición.
• 🔍 La velocidad del objeto en un tiempo específico se calcula derivando la función de posición y sustituyendo ese valor de tiempo.
• 📌 La derivada de la función de posición da el vector de velocidad en un punto específico del tiempo.
• 📍 El vector de velocidad es tangente a la trayectoria del objeto en el punto considerado.
• 🔄 La rapidez instantánea es la magnitud del vector de velocidad, que se calcula como la raíz cuadrada de la suma de las componentes al cuadrado.
• 📏 La rapidez se mide en función de las unidades de la posición y el tiempo, como metros por segundo o pies por segundo.
• 🔢 La magnitud de un vector bidimensional se calcula usando el teorema de Pitágoras, y es aplicable para vectores tridimensionales también.
• 🙏 El script concluye agradeciendo a los miembros de YouTube y Patreon por su apoyo.

Q & A

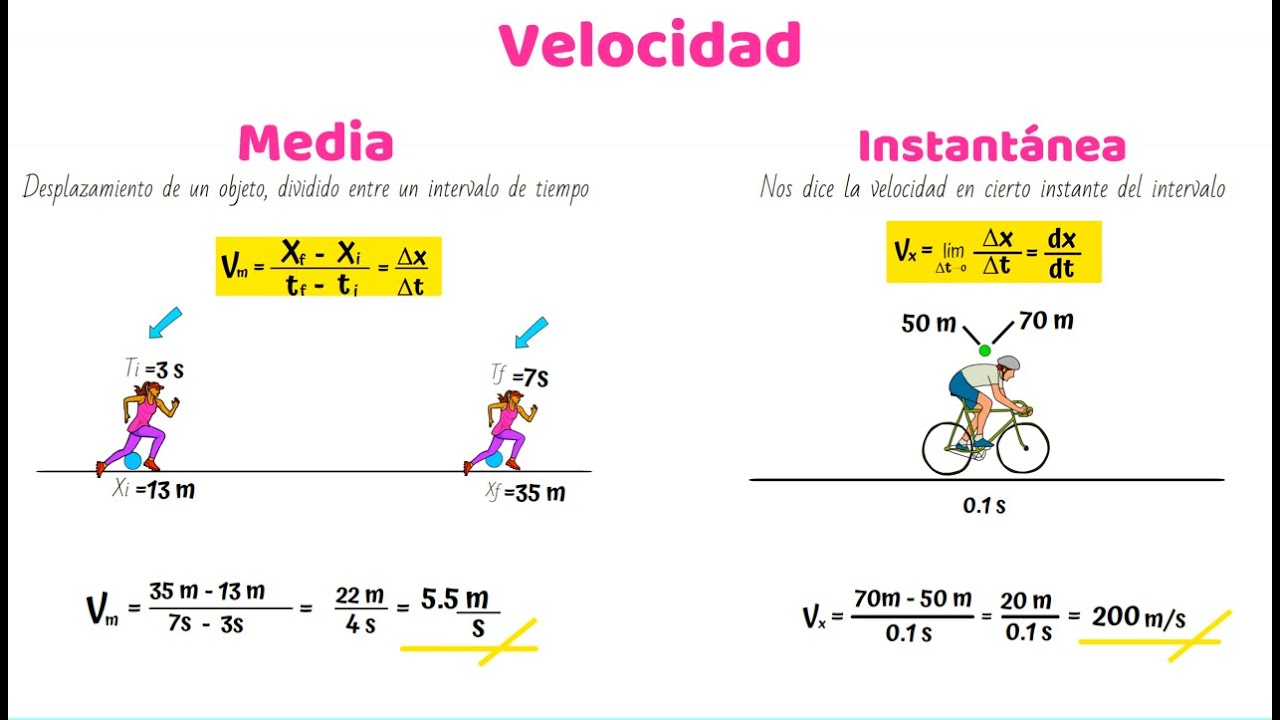
¿Cómo se calcula la velocidad instantánea de un objeto?

Para calcular la velocidad instantánea de un objeto, necesitamos conocer su posición en función del tiempo. Esto se hace derivando la función que describe la posición del objeto en términos del tiempo.

Si la posición de un objeto se describe por la función \( t^2 \), ¿cuál es la posición en t=0 y t=1?

En t=0, la posición es \( 0^2 = 0 \). En t=1, la posición es \( 1^2 = 1 \).

Si la posición de un objeto se describe por la función \( t^2 \), ¿cuál es la posición en t=2?

En t=2, la posición es \( 2^2 = 4 \).

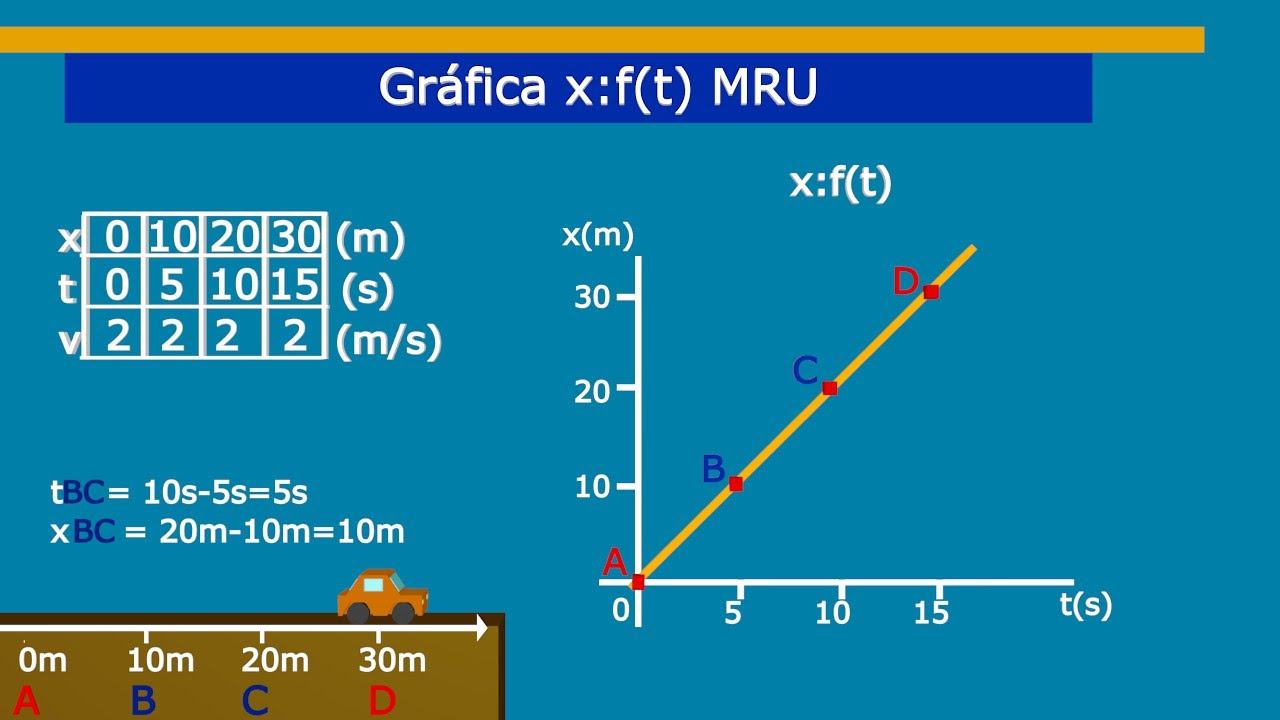
¿Cómo se representa la trayectoria de un objeto en un plano cartesiano si se conoce su posición en función del tiempo?

Se puede representar trazando los puntos correspondientes a diferentes valores de tiempo en el plano cartesiano, donde los ejes x e y representan las coordenadas de la posición del objeto.

Si la función de posición es \( t^2 \), ¿cuál es la velocidad del objeto en t=1?

La velocidad se calcula derivando la función de posición, lo que nos da \( 2t \). Sustituyendo t=1, la velocidad es \( 2 \cdot 1 = 2 \).

¿Cómo se interpreta el vector de velocidad en relación con la trayectoria del objeto?

El vector de velocidad es tangente a la trayectoria en el punto correspondiente al tiempo t, indicando la dirección y magnitud de la velocidad instantánea del objeto en ese instante.

¿Cuál es la rapidez instantánea si la velocidad es el vector (1, 2)?

La rapidez instantánea es la magnitud del vector de velocidad, que se calcula como \(\sqrt{1^2 + 2^2} = \sqrt{5}\).

¿Cómo se calcula la magnitud de un vector en términos de sus componentes?

La magnitud de un vector se calcula sumando el cuadrado de cada componente y luego tomando la raíz cuadrada del resultado, basado en el teorema de Pitágoras.

¿Cómo varía la unidad de medida de la velocidad si la posición se mide en metros y el tiempo en segundos?

Si la posición se mide en metros y el tiempo en segundos, la unidad de medida de la velocidad será metros por segundo (m/s).

¿Qué diferencia hay entre la velocidad y la rapidez en el contexto del script?

La velocidad es un vector que indica tanto la magnitud como la dirección de un objeto en movimiento, mientras que la rapidez es la magnitud del vector de velocidad, es decir, la velocidad sin considerar la dirección.