Similar Triangles - GCSE Maths

Summary

Este video educativo explora el concepto de triángulos similares, presentando dos tipos de problemas: triángulos conectados y triángulos superpuestos. Se explica cómo determinar la relación de escala constante entre los lados correspondientes de los triángulos y cómo usar la similitud para resolver problemas. Se destacan técnicas como la división de lados en el mismo triángulo y la utilización de fracciones equivalentes. Además, se abordan problemas prácticos con triángulos conectados y superpuestos, y se muestra cómo aplicar la similitud y las proporciones para encontrar longitudes desconocidas en triángulos.

Takeaways

• 🔍 El vídeo trata sobre triángulos similares y cómo resolver problemas donde los triángulos están conectados o se superponen.
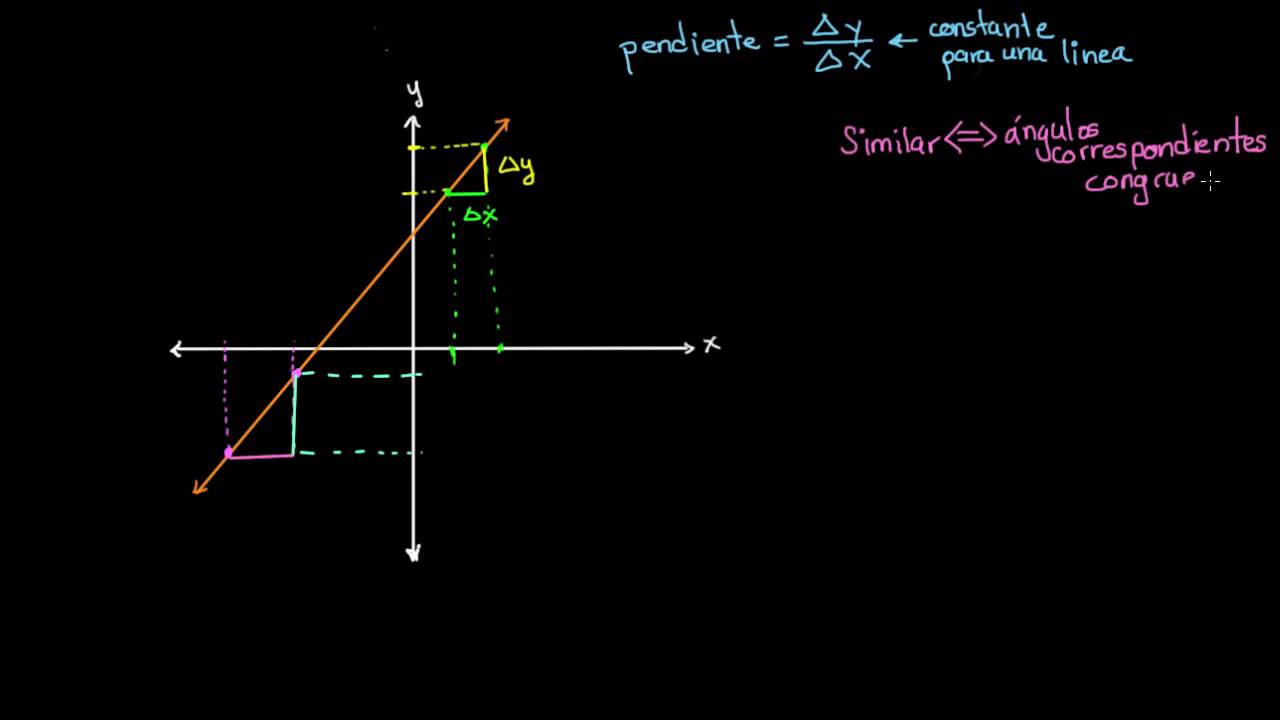
• 🔄 Para que dos triángulos sean similares, deben tener una relación de escalado constante entre sus lados correspondientes.
• 📏 El factor de escala se puede encontrar dividiendo los lados correspondientes de los triángulos, y siempre dará el mismo valor.
• ↔️ El factor de escala también se puede encontrar al dividir los lados dentro del mismo triángulo, siempre que se dividan de manera consistente.
• 🔼 Al resolver problemas con triángulos similares, se pueden utilizar ángulos verticalmente opuestos y ángulos alternos para demostrar la similitud.
• 📐 La similitud de triángulos se puede demostrar al superponer triángulos y comparar los ángulos correspondientes.
• 🔢 Para encontrar valores desconocidos en triángulos similares, se establecen fracciones de lados correspondientes y se resuelven ecuaciones.
• 📏 En problemas donde los triángulos se superponen, se identifican las longitudes de los lados correspondientes y se resuelven ecuaciones para encontrar longitudes desconocidas.
• 💡 Es importante ser consistente al establecer fracciones al inicio de un problema, ya que afecta la resolución de la ecuación.
• 📋 En problemas con ratios dados, se pueden asignar longitudes ficticias a los lados en proporción para facilitar el cálculo de longitudes desconocidas.

Q & A

¿Qué son los triángulos similares y cómo se definen?

Los triángulos similares son dos triángulos que tienen las mismas proporciones y las mismas formas, pero no necesariamente el mismo tamaño. Se definen por tener un factor de escala constante para la ampliación o reducción de uno a otro, y por tener todos sus ángulos correspondientes iguales.

¿Cómo se determina si dos triángulos son similares?

Para determinar si dos triángulos son similares, se verifica que sus ángulos correspondientes sean iguales y que la proporción de sus lados correspondientes sea constante. Esto se puede hacer dividiendo los lados correspondientes de uno de los triángulos por los lados correspondientes del otro triángulo y ver si el resultado es el mismo para todos los pares de lados.

¿Qué es el factor de escala de amplificación y cómo se calcula?

El factor de escala de amplificación es el número por el cual se multiplica el lado de un triángulo para obtener el lado correspondiente en el otro triángulo similar. Se calcula dividiendo un lado del triángulo más grande por el lado correspondiente del triángulo más pequeño.

Si dos triángulos son similares, ¿qué relación tienen sus lados?

Si dos triángulos son similares, los lados correspondientes están en la misma proporción, lo que significa que si se toma cualquier par de lados en uno de los triángulos y se divide el lado más grande entre el lado más pequeño, el resultado será el mismo que para cualquier otro par de lados en los triángulos.

¿Cómo se resuelven problemas donde los triángulos están conectados?

Para resolver problemas donde los triángulos están conectados, se identifican los lados correspondientes y se establecen las relaciones de proporción utilizando el factor de escala de amplificación. Luego, se resuelven las ecuaciones para encontrar los valores desconocidos, asegurándose de que los factores de escala se apliquen consistentemente.

En problemas donde los triángulos se solapan, ¿cómo se demuestra que son similares?

En problemas donde los triángulos se solapan, se demuestran similares al mostrar que tienen todos los ángulos correspondientes iguales, ya sea por ser ángulos alternos o por tener lados paralelos que forman ángulos verticales opuestos.

¿Cómo se utilizan las proporciones para encontrar lados desconocidos en triángulos similares?

Se establecen fracciones con los lados correspondientes y se resuelven las ecuaciones para encontrar los lados desconocidos. Es importante ser consistente en la selección de lados para las fracciones, ya sea siempre poniendo el triángulo más pequeño en la parte superior o siempre en la parte inferior.

¿Qué sucede si se tiene una relación de longitudes dada en un problema de triángulos similares?

Si se tiene una relación de longitudes dada, como 5 a 4, se puede asumir una longitud para cada lado en proporción y luego se utilizan estas longitudes para establecer fracciones y resolver las ecuaciones para encontrar los lados desconocidos.

¿Cómo se abordan los problemas donde los triángulos tienen longitudes totales conocidas y partes desconocidas?

Se identifican las longitudes totales y se establecen ecuaciones para las partes desconocidas, utilizando las proporciones de los lados correspondientes de los triángulos similares. Se resuelven estas ecuaciones para encontrar los valores de las longitudes desconocidas.

¿Cómo se pueden usar las fracciones para resolver problemas de triángulos similares?

Las fracciones se usan para establecer relaciones de proporción entre los lados correspondientes de los triángulos similares. Se forman fracciones con los lados y se resuelven las ecuaciones resultantes para encontrar los valores desconocidos, asegurándose de que las fracciones sean consistentes en su estructura.

Outlines

00:00

📐 Introducción a los Triángulos Similares

Este primer párrafo introduce el concepto de triángulos similares, explicando que para que dos triángulos sean similares, deben existir una relación constante de escalado entre sus lados correspondientes. Se ilustra con un ejemplo de dos triángulos donde la relación de similitud se demuestra al multiplicar los lados de uno por dos para obtener los lados del otro. Además, se mencionan otras observaciones, como el cálculo del factor de escala y la consistencia en los fracciones equivalentes que se pueden obtener al dividir los lados dentro de los mismos triángulos o entre triángulos similares.

05:01

🔍 Triángulos Similares y Puntos en Paralelo

Este segmento se enfoca en problemas donde los triángulos están conectados a través de líneas paralelas. Se destaca la importancia de los ángulos verticalmente opuestos y los ángulos alternos, que son iguales cuando las líneas están paralelas. Se resuelve un ejemplo donde se encuentran los valores perdidos de los lados de los triángulos, utilizando tanto la multiplicación directa como la resolución de fracciones para encontrar las soluciones. Se enfatiza la consistencia en la forma de establecer las fracciones al inicio del problema.

10:02

🧩 Solución de Problemas con Triángulos Overlapped

En este apartado, se aborda cómo resolver problemas donde los triángulos se solapan. Se demuestra la similitud de los triángulos a través de la comparación de sus ángulos correspondientes. Se presenta un ejemplo donde se identifican los lados correspondientes y se resuelven los valores perdidos de los lados X e Y utilizando la técnica de las fracciones y la consistencia en la elección de los pares de lados. Se resalta la importancia de la consistencia en la selección de lados para establecer las fracciones y se resuelven los valores de X e Y.

15:03

🔢 Utilizando Proporciones en Triángulos Similares

Finalmente, se presenta un desafío más complejo que involucra proporciones en triángulos similares. Se describe un escenario donde se conoce la proporción de lados de un triángulo y se debe encontrar la longitud de uno de sus lados. Se utiliza una estrategia de resolución donde se asume una longitud para los lados en proporción y se resuelve el problema como se habría hecho con longitudes reales. Se resalta la utilidad de esta técnica para resolver problemas en exámenes, y se resuelve un ejemplo específico donde se encuentra la longitud de un lado desconocido.

📚 Conclusión y Recomendaciones para Práctica

El último párrafo ofrece una conclusión del video y recomienda al espectador explorar más videos relacionados, suscribirse para no perderse futuros contenidos y practicar con preguntas de exámenes en el tema. Se invita a los espectadores a intentar resolver problemas similares para fortalecer su comprensión y habilidad en el uso de triángulos similares.

Keywords

💡Triángulos similares

Los triángulos similares son aquellos que tienen las mismas formas pero pueden tener diferentes tamaños. En el vídeo, se discute cómo dos triángulos pueden ser similares si existe una constante de escalado entre ellos, lo que significa que sus lados corresponden en una relación de proporcion constante. Esto es fundamental para entender cómo se relacionan las medidas de los triángulos en los problemas presentados en el vídeo.

💡Escala de ampliación

La escala de ampliación es el factor por el cual se multiplica el tamaño de un triángulo para obtener el tamaño del otro. En el guion, se menciona que si los lados de dos triángulos similares son 12 y 24, respectivamente, la escala de ampliación es 2, ya que 12 se convierte en 24 al multiplicar por 2. Esta noción es crucial para resolver problemas donde se requiere encontrar la medida de un lado desconocido en un triángulo similar.

💡Lados correspondientes

Los lados correspondientes en dos triángulos similares son los que se alinean vertical u horizontalmente y tienen la misma relación de proporción. El guion utiliza este concepto para demostrar cómo se pueden encontrar las proporciones entre los lados de los triángulos, lo cual es esencial para resolver problemas de similaridad.

💡Ángulos verticalmente opuestos

En el vídeo se menciona que los ángulos verticalmente opuestos son iguales, lo que es una propiedad geométrica que se utiliza para demostrar la similaridad entre triángulos. Esto se aplica en problemas donde los triángulos están conectados o superpuestos, y es fundamental para establecer la relación de similaridad entre ellos.

💡Ángulos alternos

Los ángulos alternos son aquellos que se forman cuando una línea paralela intersecta dos líneas secundarias. En el guion, se utiliza la propiedad de que los ángulos alternos son iguales para demostrar la similaridad entre triángulos que están conectados por líneas paralelas. Esta es una técnica común en la geometría para probar la similaridad.

💡Fracciones equivalentes

Las fracciones equivalentes son aquellas que, aunque diferentes en su numeración, representan la misma cantidad. En el contexto del vídeo, se menciona que hay muchas fracciones equivalentes que se pueden escribir usando triángulos similares, lo que ayuda a resolver problemas más complicados.

💡Relación de proporcion

La relación de proporcion es la relación numérica entre dos cantidades. En el guion, se utiliza la relación de proporcion para resolver problemas donde se conoce la relación entre lados de triángulos similares, como en el caso donde la relación entre dos lados es 5:4. Esto es esencial para encontrar la medida de un lado desconocido.

💡Problemas de triángulos conectados

Los problemas de triángulos conectados son aquellos en los que dos triángulos están unidos a lo largo de uno o más lados. El guion describe cómo se pueden usar las propiedades de los triángulos similares para resolver problemas donde se conocen algunas medidas y se busca encontrar otras.

💡Problemas de triángulos superpuestos

Los problemas de triángulos superpuestos son aquellos en los que dos triángulos comparten parte de su área. El vídeo aborda cómo se pueden usar las propiedades de los triángulos similares para resolver problemas donde se conocen algunas medidas y se busca encontrar otras, incluso cuando los triángulos están superpuestos.

💡Ecuaciones de dos pasos

Las ecuaciones de dos pasos son aquellas que requieren dos operaciones para resolverlas, como la eliminación de términos o la simplificación de fracciones. En el guion, se utilizan ecuaciones de dos pasos para encontrar la medida de lados desconocidos en triángulos similares, lo que es un método común en la resolución de problemas geométricos.

Highlights

Exploración de triángulos similares y dos tipos de problemas: triángulos conectados y triángulos superpuestos.

Definición de triángulos similares basada en una constante de escala constante entre ellos.

Demostración de similitud triangular mediante la multiplicación de longitudes de lado correspondientes.

Observaciones sobre cómo encontrar la constante de escala a través de la división de pares de lados correspondientes.

Ejemplo práctico de cómo dividir lados dentro del mismo triángulo para encontrar la constante de escala.

Importancia de las fracciones equivalentes en los triángulos similares para resolver problemas más complejos.

Análisis de triángulos conectados con líneas paralelas y cómo esto afecta la similitud.

Uso de ángulos verticalmente opuestos y ángulos alternos para demostrar similitud en triángulos conectados.

Técnica para encontrar longitudes desconocidas en triángulos similares conectados mediante la multiplicación y la división.

Enfoque alternativo para resolver problemas de triángulos similares utilizando fracciones y la consistencia en la selección de lados.

Solución de problemas de triángulos superpuestos utilizando la similitud y la correspondencia de ángulos.

Estrategia para manejar longitudes de lados en triángulos superpuestos y cómo encontrar longitudes desconocidas.

Uso de la consistencia en la formación de fracciones al resolver problemas de triángulos similares superpuestos.

Resolución de problemas con triángulos similares y ratios dados, utilizando la técnica de asumir longitudes para los ratios.

Ejemplo de cómo asumir longitudes para ratios ayuda a encontrar la longitud de un lado desconocido en un triángulo.

Conclusión del video con una revisión de los conceptos y la recomendación de intentar problemas de exámenes relacionados.

Transcripts

[Music]

in this video we're going to look at

similar triangles we're going to look at

two types of problem one's where the

triangles are connected like this one

and ones where they overlap like this

one here before we do this we're going

to take a closer look at what it means

for two triangles to be similar take

these two triangles here if these two

triangles are similar there must be a

constant scale for out of enlargement

from one to the other so if we match up

the corresponding sides on the base here

we have 12 and 24 on the left we have 5

and 10 for the height and the hypotenuse

of these are 13 and 26 to get from 12 to

24 we'd multiply by two this is the same

as going from 5 to 10 on the height and

also for the hypotenuse from 13 to 26

since this is always the same number

these shapes must be similar it works in

the other direction as well so if we go

from 24 to 12 we would multiply by 1/2

and and this is the same for the other

sides as well so we know these two

shapes are similar there are some other

observations we can make we can find

that scale factor of enlargement by

dividing the pairs of corresponding

sides so if we take the purple sides 24

and 12 and divide them you'll see we get

two this works for the other pairs of

sides as well so 10id 5 that's also 2

and 26id 13 that's once again two but it

also works the other way around so if we

take those fractions and do the

reciprocal like

this then these will always give you the

same value as well which this time is

1/2 in these fractions here we divided

one side from one of the triangles by

the corresponding side on the other

triangle but we can actually just divide

sides within the same triangle as well

so if we take the green side in the

small triangle and divide it by the

purple side we get 5 over2 and then if

we do the same thing in the larger

triangle the green side divid by the

purple side that's 10id 24 these two

fractions actually give the same value

and it will be the same for any of the

pairs of sides as long as you're

consistent in what you do for instance

if I take the blue side and divide it by

the green side and then do the same on

the second triangle blue divide by Green

I get the same number once again these

two fractions give the same value or I

could have done the purple side divide

by the blue side so we get 12 over 13 on

this one and on the other one 24/ by 26

and these also give the same value and

so do their reciprocals so if we take

all of these fractions and take the

reciprocal of them those will also be

vehicle as well so there's actually lots

and lots of equivalent fractions that

you can write down using similar

triangles this is going to be helpful in

solving some of the more complicated

questions in this

video now let's go back to the original

type of question the first one we said

was when we have two triangles that are

connected and notice we have a parallel

line at the top and at the bottom the

first thing to notice here is that this

angle here is the same as the one below

it because these are vertically opposite

angles then if we draw in this angle

here and draw on some lines like this we

find that the green angle is the same as

the green angle down here and we call

these alternate angles you can see we've

got a zed shape there the same idea

works for this angle as well so if we

draw in a zed shape here this time we

find that this blue angle is the same as

the blue angle at the bottom down here

once again due to alternate angles in

the previous video on similar shapes we

learned that when the angles are all the

same the shapes must be similar it's

even more obvious if I move this

triangle down to the bottom here and

flip it round you can see the blue

angles on the left are the same so are

the red ones at the top and the green

ones on the right but I'd also need to

move down these sides like this notice

how the sides have moved to a different

position this time if I put the original

diagram back you can see the eight was

on the right hand side but now it's on

the left hand side the 10 was on the

left and now it's on the right and the

13 was on the top and now it's on the

bottom so let's go ahead and try and

find these missing values now that we've

put this information on so to get from

10 to 20 we multiply by two so we must

multiply the 13 by two on the bottom to

get to Y and 13 * 2 is

26 then of course we must multiply the 8

by two to get to the x value and 8 * 2

is

16 now this uses the technique that we

did in the previous video on similar

shapes but I'm also going to show you

this by using fractions you don't need

to use this approach to solve these ones

but it's going to help us to practice it

especially for the questions later in

this video so what we're going to do is

pair up the corresponding sides so on

the left here we have X and 8 and on the

right we have 20 and 10 we're going to

use these pairs of sides to find the

value of X so if we divide the green

ones by doing xide by 8 this must be the

same as when we divide the blue ones so

20 over 10 so we form an equation like

this we can solve this equation by

multiplying both sides by eight if you

multiply the left side by 8 the 8 will

cancel and then you multiply the right

side by 8 we get this 20 * 8 on the top

there is 160 so we have 160 over 10

which was 16 and we knew that was the

answer to the question because we worked

it out before so so X is 16 and let's do

a similar idea to work out y so y pairs

up with the 13 on the bottom here so if

we divide the purple Sid we get y over

13 and this must be equal to any of the

other pairs divided I'm going to go for

the blue pair again so 20 over

10 here we just multiply both sides by

13 and we get 20 lots of 13 over 10 20 *

13 is 260 and divide this by 10 and you

get

26 which again we knew this was the

answer from before

now let's take a look at how a question

like this could be worded so if we take

some triangles like this and we're told

to work out the values of X and Y notice

they haven't even told us that these two

triangles are similar they don't need to

because they've marked on the parallel

lines so we should already know that

information so let's try with X first

you can see that X matches up with a 15

on the bottom then if we remember that

if we flip that triangle from the top

upside down the8 is actually going to

match up with a 12 so even though the

eight is on the right it matches up with

the 12 on the left left and the four

matches up with the Y so let's divide

the purple sides so x / 15 and this is

going to be equal to one of the other

pairs divided now since we don't know

why I'm going to avoid the blue pair and

go for the green one so the green one

would be eight IDE by 12 then we can

just solve this like we did for the

previous two we just multiply both sides

by 15 so on the left we get X and on the

right we get 8 over2 multiplied 15 which

we could combine to one fraction like

this 8 * 15 is 120 so we get x = 120 /

12 and 120 / 12 is just 10 so we found

the value of x it's 10 one thing that's

really important is you need to be

consistent in the way you set up the

fractions at the start of this question

the X here was from the smaller triangle

the eight was also from the smaller

triangle the 15 was from the larger

triangle and so was the 12 it's

important that you're consistent in

having the small on the top and the

large on the bottom or of course you

could have the large on the top and the

small on the bottom it doesn't matter

which way around you do it as long as

you're consistent I put the small on the

top here because we were trying to find

X so let's replace the X with a 10 and

let's go and find y so this time we're

going to divide the blue pair so y over

4 and this is going to be equal to one

of the other pairs I'm going to go for

the green one once again but this time

it will be 12 over 8 notice y was on the

larger triangle so 12 must also be on

the larger triangle and on the bottom

we've got four and eight which are from

the smaller triangle to solve this then

we just multiply both sides by four on

the left we'd have y and on the right 12

8 multiplied by 4 we can combine that to

one fraction so it's 12 * 4 over 8 12

fours are just 48 so it's 48 over 8 and

48 / by 8 is 6 so the value of y is

6 now let's have a look at the other

type of problem so a question that looks

like this this time the triangles are

both there but they're overlapping each

other we we can show that they're

similar Again by looking at their angles

so if we draw in these lines here then

this green angle on the left must be the

same as this green angle up here this is

because they're corresponding angles the

same idea works on the right side so if

we draw in this line and then these two

this angle here that's blue must be the

same as this one here that's blue once

again because they're corresponding

angles and then finally we have the

angle at the top here well that's

actually the same angle for both of the

triangles so if I separate them off like

this we've got the small triangle and

then the large triangle you can see all

of the angles match again so they must

be similar shapes but this one can be a

bit more tricky to do on the top

triangle I actually have lengths for all

of the sides so I've got the 15 on the

bottom the 18 on the left and the 12 on

the right on the larger triangle though

it's a bit more difficult I can see I

have 25 on the base so I can mark that

on but the left and right side can be

tricky so for the left side here it's

the whole length from here to here so we

have a y and an 18 so the total length

must be y + 18 it's similar on the right

hand side so we need to go all the way

from here to here which we have X and 12

so the total length is x + 12 now that

we form these triangles we're ready to

find the missing values of X and Y to do

this we're going to divide corresponding

pairs of sides again so I'm going to

start by trying to find X so I can see

I've got X on the larger triangle in the

x + 12 side so x + 12 and I'm going to

divide that by the side that matches on

the smaller shape which is 12 so I have

x + 12 over 12 then this is going to be

equal to a second fraction and I need to

pick another pair of sides now I'm not

going to pick the sides on the left

because they have a y in them if I pick

the base of the triangle then I can see

I have both of those sides I've got 15

and 25 I need to be consistent and since

I started with the larger triangle on

the last fraction I'll do the same here

so it's 25 on the top and 15 on the

bottom now we can go ahead and solve

this so for this one we would multiply

both sides by 12 that would give us x +

12 on the left and on the right we'd

have 25 multiplied by 12 all over 15 we

could also multiply both sides by 15 now

so if we multiply the left side by 15 we

need to use a bracket so we'd have 15

lots of x + 12 and on the right hand

side the 15s will no cancel so it's just

25 * 12 on the left I would now expand

out this bracket so 15 lots of X is 15 x

and 15 lots of 12 is 180 on the right

side I need to do 25 multip by 12 which

is 300 this is now just a nice two-step

equation to solve we can subtract 180

from both sides so we get 15x = 120 and

then divide both sides by 15 we get x =

8 so we found the value of x it's 8

cm now let's do the same idea and work

out why so we'll start with the y + 18

and divide it by the side that matches

on the other triangle which is

18 and this will be equal to another

fraction and it makes sense to choose

the sides 25 and 15 again so 25 over 15

you can see I've been consistent again

and I have the larger triangle on the

top and the smaller triangle on the

bottom of those fractions we'll solve

this in the same sort of way so we'll

multiply both sides by 18 on the left

this will give us y + 18 and on the

right 25 * by 18 all over

15 then multiply both sides by 15 so we

get 15 lots of y + 18 and on the right

the 15 cancel so it's just 25 * 18 if we

expand out the brackets here we get 15

lots of y That's Just 15 Y and 15 * 18

is

270 on the right 25 lots of 18 is 450

once again we just have a two-step

equation to solve if you subtract 270

from both sides we get 15 y = 180 and

then divide both sides by 15 and we'll

get y = 12 now let's try a second

example of this this a little bit more

difficult so this time we've got this

diagram and we're just trying to find X

so if we separate these off into two

triangles we have a small triangle that

looks like this and we can see the side

on the left there at the top is X and on

the right we have a nine then if we do

the big triangle here the side on the

top left is actually all the way from

here to here so we need to do x + 5 and

on the right this time is

12 now that we have these two triangles

we can go ahead and find X so we need to

divide the sides that match so I'm going

to divide x + 5 on the big triangle by X

on the small

triangle and this will equal another

fraction and since I started with the

larger one I'll do 12 over 9 this one's

a little bit different in its structure

but we use the same idea to solve it

let's multiply both sides by X this time

on the left this will cancel the X on

the bottom so I get x + 5 and on the

right I'll get 12 lots of X over

9 then we multiply both sides by 9 on

the left hand side this will give us 9

lots of x + 5 and on the right the N9

will cancel so we just have 12 lots of X

expanding the bracket on the left gives

us 9x + 45 and on the right 12 lots of X

is just 12 x to solve this equation we'

subtract 9x from both sides

if you subtract it from the left it will

cancel so we've just got 45 and if you

subtract 9x from 12x you get

3x then finally divide both sides by

three and you find that X is equal to 15

now I want to look at one more of these

questions but there's going to be some

ratio involved so if we take this

diagram here and notice we actually have

labels for the sides this time this is

quite common in exams especially for Ed

Exel and this time they're going to tell

us that the ratio of a d to be is 5 to 4

and we're going to be tasked with

finding the length of De

now at first glance it looks like we

don't have very much information on this

diagram we only have the 15 cm so it

might feel like we don't have enough to

answer the question but we do we're

going to start with this ratio here A D

to be being at 5: 4 now the easiest way

to think about this is just to pretend

that a d is 5 cm and that be is 4 cm

even if it doesn't look like they're

that long in the diagram it's still

going to work for the question so I'm

going to label be as four and AD as five

from here we just proceed with the

question as normal it's important that

you understand that those aren't

actually that length it's just their

ratio but for this question it will help

us solve the problem finally since we're

trying to find de I'm going to label

that as X so what we'll do now is

separate them off into the two triangles

so we have the small triangle that looks

like this that's triangle EBC and for

this triangle we know some of its

lengths from E to C is 15 and E to B is

four or at least we're pretending it's

four and for the large triangle which is

triangle da we know the height on the

left from a to d is 5 or at least we're

pretending it's five and we also know

the length all the way along the

diagonal there is x + 15 now we just go

ahead and set up some fractions again so

I'm going to start with x + 15 and

divide it by the same side on the other

triangle which is 15 then I have my

second fraction that this is equal to

and it will be 5 over

4 now we just solve this equation like

we have done all of the previous ones

multiply both sides by 15 that's x + 15

on the left and on the right 5 * 15 all

over 4 then multiply both sides by four

on the left we've got four lots of x +

15 and on the right the four will cancel

so 5 lots of

15 expand out the bracket on the left

we've got 4x + 60 and on the right 5 *

15 is

75 now solve this two-step equation by

subtracting 60 from both sides 4X will

be 15 and then finally divide both sides

by four and we'll find that X is

3.75

thank you for watching this video I hope

you found it useful check out the one I

think you should watch next subscribe so

you don't miss out on future videos and

go and try the exam questions on this

topic that are in this video's

description