Representación gráfica de intervalos | Ejemplo 2
Summary
TLDREn este video educativo, el presentador guía a los estudiantes en cómo representar intervalos en una recta numérica, abordando desafíos comunes y proporcionando estrategias para entender mejor los conceptos. Explica cómo leer y graficar intervalos complejos, como 'menos que 10', y proporciona ejemplos para aclarar la representación gráfica de intervalos que cumplen con múltiples condiciones. Además, ofrece ejercicios prácticos para fortalecer la comprensión y habilidades de los estudiantes en el tema.
Takeaways
- 📐 Los intervalos en la recta numérica se representan de manera diferente cuando la equis y el número están en posiciones opuestas.
- 🔄 Para representar intervalos donde la equis está a la derecha del número, se invierte el orden y se cambia el signo de comparación.
- 📉 Los intervalos que incluyen el número (con el símbolo de igual) se marcan con un huequito o corchete, mientras que los que no lo incluyen se marcan con un paréntesis o signo de exclamación.
- ➡️ Al graficar intervalos, se inicia en la parte izquierda marcada y se termina en la derecha, siguiendo las reglas de inclusión o exclusión del número.
- 🚫 Si el intervalo no incluye el número 10, se marca con un huequito o se indica con un paréntesis abierto para mostrar la exclusión.
- ↔️ En los intervalos que se leen de derecha a izquierda, como 'menor que 10', se cambian todos los elementos y el signo para representar correctamente en la recta numérica.
- 📌 Al graficar, se marca con una línea recta hacia la izquierda para los intervalos que son menores que un número específico, y hacia la derecha para los mayores.
- 🔢 En los casos donde se presentan múltiples condiciones, se busca la intersección en la recta numérica donde se cumplen todas las condiciones.
- 📋 Se pueden utilizar diferentes métodos para marcar los intervalos en la recta numérica, como líneas, puntos o paréntesis, siempre y cuando se indique claramente la inclusión o exclusión de los números.
- 📘 La representación de intervalos en la recta numérica es crucial para entender y resolver problemas matemáticos que involucran condiciones y rangos de números.
Q & A
¿Qué es lo que se busca enseñar en este curso de intervalos?
-El curso busca enseñar a los estudiantes cómo representar intervalos en una recta numérica y cómo abordar los ejercicios que son más difíciles de entender, especialmente aquellos que no se pueden leer de manera directa en la recta.
¿Cómo se debe leer un intervalo donde la equis está en el medio y el número está al final?
-En este caso, no se puede leer de la forma habitual. Por ejemplo, si la equis está en el medio y el número 10 está al final, se leería como 'los números mayores que 10'.
¿Qué estrategia se sugiere para representar intervalos donde la x está en el medio y el número está al final de la recta?
-La estrategia sugerida es cambiar el orden de todo al revés, escribiendo primero la equis y luego el número, y también invertir el signo para que quede 'menor que' en lugar de 'mayor que'.
¿Cómo se representa gráficamente un intervalo de números menores que 10 en la recta numérica?
-Primero se traza la recta y se ubica el número 10. Luego se marca hacia la izquierda de la recta para indicar que son números menores que 10. Se puede hacer con líneas, rayitas o un marcador específico, como un huequito o un paréntesis, para indicar que el 10 no está incluido.
¿Cuál es la diferencia entre un intervalo que incluye el número y uno que no lo incluye?
-Si el intervalo incluye el número, se utiliza un corchete para indicar que lo incluye. Si no lo incluye, se utiliza un paréntesis. Esto se basa en si el intervalo está mayor o menor que el número en cuestión.
¿Cómo se determina la intersección de dos intervalos en la recta numérica?
-Para encontrar la intersección de dos intervalos, se identifican los puntos donde ambas líneas están presentes en la recta. Esa es la parte donde los intervalos cumplen ambas condiciones.
¿Qué significa una flecha en la recta numérica al representar un intervalo?
-Una flecha en la recta numérica indica que el intervalo continúa indefinidamente en la dirección de la flecha, generalmente hacia el infinito.
¿Cómo se representa un intervalo que no tiene solución en la recta numérica?
-Si un intervalo no tiene solución, se puede representar como un conjunto vacío, lo que se puede escribir de varias formas, como un intervalo que no incluye ningún número o simplemente señalando que no hay respuesta.
¿Qué tipo de ejercicios se proponen al final del curso para la práctica?
-Se proponen ejercicios que requieren ordenar y graficar intervalos de diferentes formas, como 'menores o iguales que siete tercios', 'menores que doce', 'menores o iguales que cero', y 'menores que tres', entre otros.
¿Dónde pueden encontrarse los recursos adicionales para aprender más sobre intervalos?
-Los recursos adicionales para aprender más sobre intervalos pueden encontrarse en el canal del instructor, en el enlace de la descripción del video o en la tarjeta que se proporciona en la parte superior del video.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados
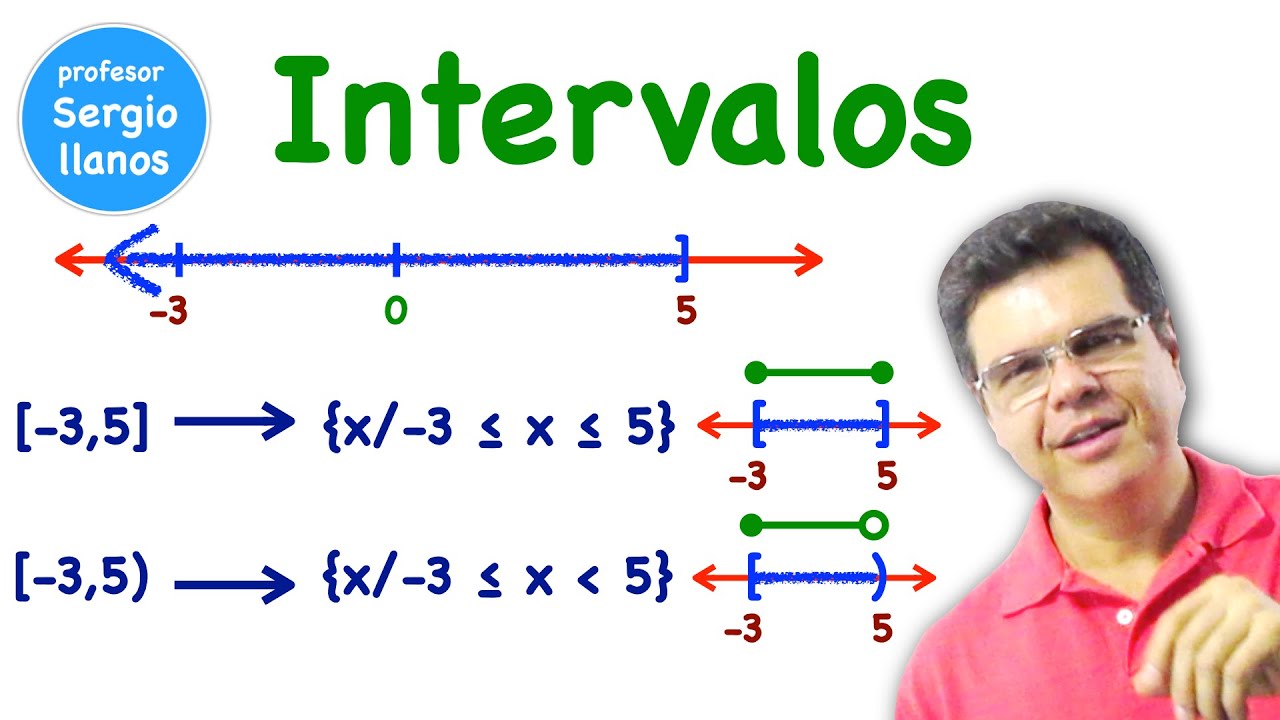
Notación de intervalos
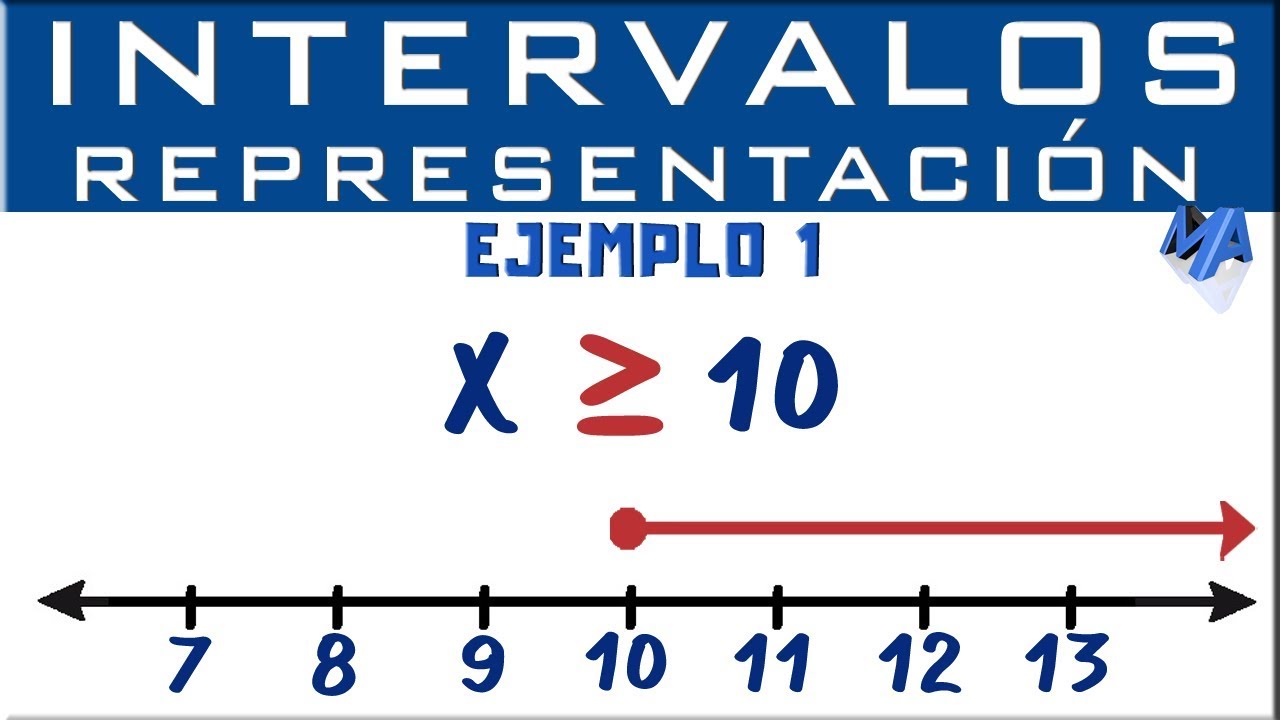
Representación gráfica de intervalos | Ejemplo 1
CONSTRUCION DE INTERVALOS MEDIANTE SIMBOLOS DE RELACION.

Números decimales en la recta numérica

Intersección de intervalos | Operaciones con intervalos

Clasificación de los NÚMEROS REALES | Naturales, Enteros, Racionales e Irracionales
5.0 / 5 (0 votes)