CONSTRUCION DE INTERVALOS MEDIANTE SIMBOLOS DE RELACION.
Summary
TLDREste tutorial educativo aborda la identificación y construcción de intervalos en matemáticas, explicando cómo se representan en una recta numérica. Se detallan los conceptos de intervalos abiertos y cerrados, y se ilustran con ejemplos cómo se construyen intervalos a partir de condiciones como 'mayor que' y 'menor o igual que'. Se enseña a interpretar correctamente los extremos de los intervalos, utilizando notación como corchetes y paréntesis para indicar si los extremos están incluidos o no.
Takeaways
- 📘 El tutorial explica cómo identificar y construir intervalos a partir de restricciones.
- 🔢 Se describe cómo construir un intervalo de números reales mayores que 2, utilizando la recta numérica.
- 📌 Se entiende que el intervalo abierto se representa con corchetes y no incluye los extremos.
- ➡️ Se aprende que 'x mayor que 2' se representa en la recta numérica como una región a la derecha del 2.
- 📐 Se detalla cómo construir un intervalo cerrado por la izquierda y abierto por la derecha, como en 'menor o igual que 1'.
- 👉 Se muestra que el intervalo 'menor o igual que 1' incluye el 1 y extiende desde menos infinito hasta 1.
- 📉 Se discute la construcción de intervalos con múltiples condiciones, como 'mayor o igual que -2' y 'menor o igual que 1'.
- 📍 Se aprende a ubicar los extremos de los intervalos en la recta numérica para comprender sus límites.
- 🔄 Se entiende la importancia de los extremos en la notación de intervalos y cómo determinan si son abiertos o cerrados.
- 💡 Se resalta que la construcción de intervalos es fundamental para entender las restricciones en matemáticas y problemas reales.
Q & A
¿Qué es un intervalo en matemáticas?
-Un intervalo es un conjunto de números reales que se extiende entre dos extremos, que pueden ser inclusivos o exclusivos.
¿Cómo se identifica un intervalo abierto en la recta numérica?
-Un intervalo abierto se identifica en la recta numérica cuando los extremos no son incluidos, se representa con paréntesis.
¿Qué significa cuando decimos que un número es 'mayor que 2' en un intervalo?
-Decir que un número es 'mayor que 2' en un intervalo significa que el intervalo comienza después del número 2 y se extiende hacia el infinito.
¿Cuál es la notación para representar un intervalo que comienza en 2 y se extiende hacia el infinito?
-El intervalo que comienza en 2 y se extiende hacia el infinito se representa como (2, +∞).
¿Cómo se construye un intervalo donde los números son menores o iguales a 1?
-Para construir un intervalo donde los números son menores o iguales a 1, se marcan todos los puntos en la recta numérica desde -∞ hasta 1, incluyendo el 1.
¿Qué tipo de intervalo es aquel que incluye -∞ y termina en 1?
-Es un intervalo cerrado por la derecha y abierto por la izquierda, se representa con corchetes y paréntesis: (-∞, 1].
¿Cómo se interpreta el intervalo que es 'mayor o igual que -2 pero menor o igual que 1'?
-Este intervalo incluye todos los números reales que son mayores o iguales a -2 y menores o iguales a 1, se representa con corchetes y cerrado en ambos extremos: [-2, 1].
¿Qué se entiende por 'extremos de un intervalo'?
-Los extremos de un intervalo son los puntos inicial y final que definen el intervalo, pueden ser inclusivos (cerrados) o exclusivos (abiertos).
¿Cómo se representa gráficamente un intervalo cerrado en ambos extremos?
-Un intervalo cerrado en ambos extremos se representa gráficamente con corchetes en ambos puntos, indicando que ambos extremos están incluidos.
¿Cuál es la diferencia entre un intervalo cerrado y un intervalo abierto?
-Un intervalo cerrado incluye a sus extremos, mientras que un intervalo abierto no incluye a sus extremos. Esto se representa con corchetes para cerrados y paréntesis para abiertos.
Outlines

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraMindmap

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraKeywords

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraHighlights

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraTranscripts

Esta sección está disponible solo para usuarios con suscripción. Por favor, mejora tu plan para acceder a esta parte.
Mejorar ahoraVer Más Videos Relacionados

Adición de Números con Signos Diferentes | Recta Numérica

Representación gráfica de intervalos | Ejemplo 2

𝗜𝗻𝘁𝗲𝗿𝘃𝗮𝗹𝗼𝘀 : Definición y ejemplos

Ubicar fracciones negativas en la recta numérica
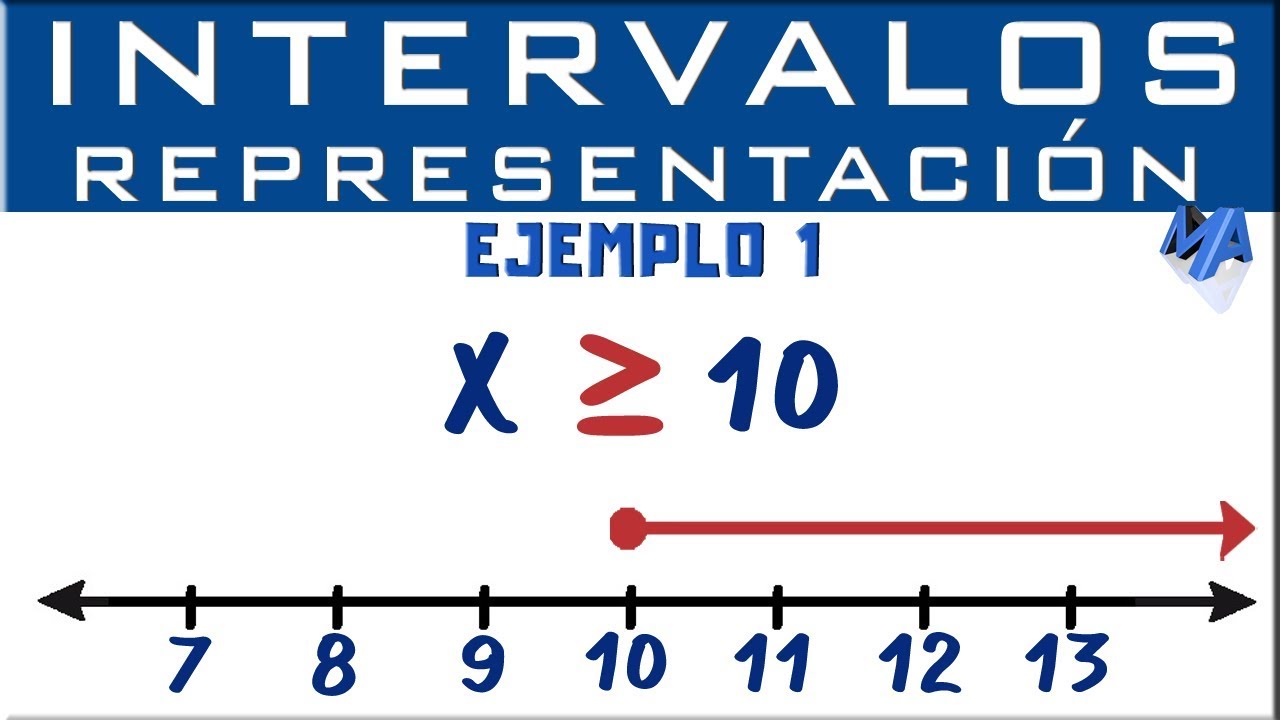
Representación gráfica de intervalos | Ejemplo 1
Intervalos - Abiertos / Cerrados / Semiabiertos - Ejercicios Resueltos
5.0 / 5 (0 votes)