Cyclotron frequency | Moving charges & magnetism | Physics | Khan Academy

Khan Academy India - English

23 Dec 202110:25

Summary

TLDRThis script explores the functioning of cyclotrons, devices that accelerate charged particles using oscillating electric and magnetic fields. It delves into the crucial timing of the electric field's oscillation, which must match the particle's spiraling motion to maintain constant acceleration. The script explains the calculation of the cyclotron's frequency, emphasizing the importance of a constant frequency for proper operation. It also touches on the relativistic effects that become significant at near-light speeds, which challenge the cyclotron's design by altering the particle's mass and thus the required oscillator frequency, leading to the development of synchrotrons for high-speed particle acceleration.

Takeaways

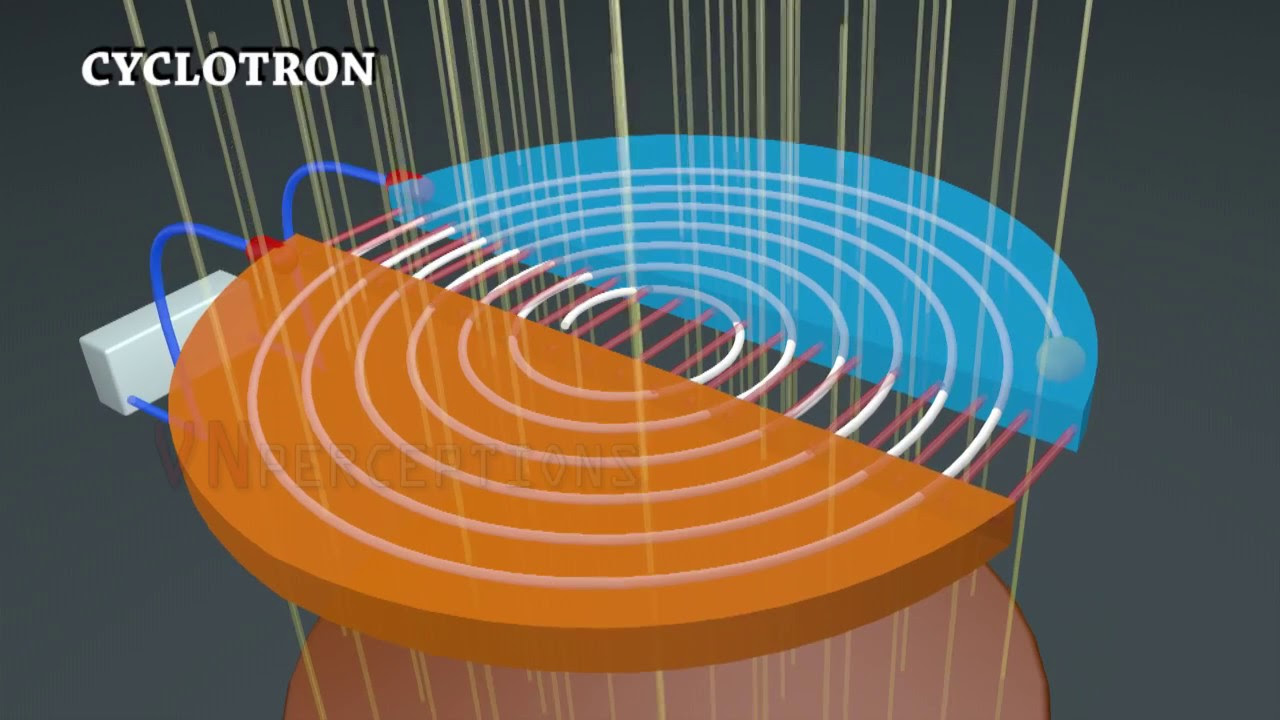
🔋 Cyclotrons use oscillating electric fields to accelerate charged particles, with magnetic fields helping to turn the particles and re-enter the electric field for continuous acceleration.
🕒 The electric field in a cyclotron must flip at the right moment to ensure the particle is accelerated at each turn, which is synchronized with the particle's spiral motion.
🔄 The frequency of the electric field flipping should remain constant because the time taken to complete one spiral remains the same, despite the increasing radius due to increasing speed.
⚙️ The time for one oscillation of the electric field is equal to the time for one spiral of the particle, which is a crucial synchronization for the cyclotron's operation.
📉 The time taken to complete half a circle (or one spiral) does not change as the particle accelerates, because the increase in distance is proportionate to the increase in speed.
🔢 The time for one full spiral can be calculated using the formula \( \frac{2\pi m}{qB} \), where \( m \) is the mass of the particle, \( q \) is the charge, and \( B \) is the magnetic field strength.
🔡 The frequency of the oscillator in a cyclotron, often called the cyclotron frequency, is the reciprocal of the time for one full spiral and is given by \( \frac{qB}{2\pi m} \).
🌀 The spiral motion of particles in a cyclotron is a result of the balance between the Lorentz force due to the magnetic field and the centripetal force required for circular motion.
🚀 Cyclotrons are limited by Einstein's theory of relativity, as the increasing mass of particles at speeds close to the speed of light affects the constant frequency of the oscillator.
🔄 Modern accelerators, such as synchrotrons, can adjust the oscillator frequency to accommodate relativistic effects and allow particles to reach speeds closer to the speed of light.
🛠 Understanding the principles of cyclotrons is fundamental to grasping the operation of more advanced particle accelerators and their limitations.

Q & A

What is the basic principle behind the operation of a cyclotron?
-A cyclotron accelerates charged particles using oscillating electric fields. As the particles move, a magnetic field causes them to turn and re-enter the electric field, allowing for continuous acceleration in a spiral path until they reach the maximum radius and are ejected at high speed.
Why is it important for the electric field in a cyclotron to flip at the right moment?
-The electric field must flip at the right moment to ensure that the charged particles are continuously accelerated. If the field does not flip in sync with the particle's motion, the particles will not gain the necessary speed to continue their spiral path and reach the maximum radius.
Should the frequency of the electric field flipping in a cyclotron be constant or changing?
-The frequency should remain constant. This is because the time it takes for a particle to complete one spiral remains the same as it spirals outwards, due to the proportional increase in both the distance (radius) and the speed of the particle.
How can the frequency at which the electric field should flip be calculated for a cyclotron?
-The frequency can be calculated using the formula for the cyclotron frequency, which is the reciprocal of the time period of one full spiral. The time period is given by "T = 2πm/qB", where "m" is the mass of the particle, "q" is the charge, and "B" is the magnetic field strength. The frequency "f" is then "f = qB/2πm".
What is the significance of the time it takes for a proton to complete one spiral in a cyclotron?
-The time it takes for a proton to complete one spiral is crucial because it determines the time period of the oscillator. This time period must be constant for the cyclotron to function properly, as it dictates the frequency at which the electric field must flip to keep accelerating the proton.
Why does the time taken to complete a half-circle or a full circle in a cyclotron remain constant?
-The time remains constant because the increase in the path length (circumference) as the proton spirals outwards is proportionate to the increase in its speed. This means that the time taken, which is the ratio of distance to speed, does not change.
What is the major limitation of cyclotrons when it comes to accelerating particles to very high speeds?
-The major limitation is the effect of Einstein's theory of relativity, where mass increases with velocity as particles approach the speed of light. This increase in mass affects the required oscillator frequency, which must be adjusted if particles are to be accelerated to speeds close to the speed of light.
How do modern accelerators overcome the limitations of cyclotrons at high speeds?
-Modern accelerators, such as synchrotrons or synchro-cyclotrons, adjust the frequency of the oscillator as the particles spiral out. This ensures that the acceleration process remains in sync with the increasing speed of the particles.
What is the relationship between the mass of a particle, its charge, the magnetic field, and the time it takes to complete a spiral in a cyclotron?
-The time it takes to complete a spiral is directly proportional to the mass of the particle and inversely proportional to the product of its charge and the magnetic field strength. This relationship is constant for a given cyclotron setup, ensuring a constant time period for the oscillator.
Why is the speed of a particle in a cyclotron proportional to the radius of its path?
-The speed of a particle is proportional to the radius because the magnetic force acting as the centripetal force is given by "F = qvB", where "v" is the speed and "r" is the radius. Rearranging this formula shows that "v = qBr/m", indicating that speed increases with radius as the particle spirals outwards.

Outlines

00:00

🔋 Cyclotron Acceleration and Oscillator Timing

This paragraph discusses the operation of cyclotrons, which use oscillating electric fields to accelerate charged particles. The particles are steered in a spiral path by a magnetic field, allowing them to repeatedly pass through the electric field and gain speed. The key challenge for engineers is to synchronize the flipping of the electric field with the particle's spiral motion. The speaker explores the concept of the oscillator frequency required for the electric field to flip at the right moment, emphasizing the need to calculate this frequency to ensure the cyclotron functions correctly. The paragraph concludes with the realization that the time taken for a particle to complete one spiral is equal to the time for one complete oscillation of the electric field, which is crucial for maintaining constant acceleration.

05:01

🌀 Constant Oscillation Frequency in Cyclotrons

The speaker delves into the specifics of cyclotron operation, explaining that the time it takes for a proton to complete a spiral remains constant despite the increasing radius of the path. This is because the increase in path length is compensated by an increase in the proton's velocity, keeping the travel time the same. Mathematically, the time for half a circle is derived to be πr/v, where r is the radius, v is the velocity, and other variables are constants. Since the radius is proportional to the velocity (r = mv/qB), the time taken for a full spiral is 2πm/qB, which is independent of the spiral's size. This leads to the conclusion that the oscillator frequency must remain constant, calculated as the reciprocal of the time for a full spiral, which is a fundamental aspect of cyclotron operation.

10:01

🚀 Limitations of Cyclotrons and the Introduction of Synchrotrons

The final paragraph addresses the limitations of cyclotrons due to the effects of Einstein's theory of relativity, which states that mass increases with velocity as particles approach the speed of light. While this effect is negligible at lower speeds, it becomes significant at speeds close to light, causing the oscillator frequency to change. This means that traditional cyclotrons are only effective at speeds much lower than the speed of light. To overcome this limitation, modern accelerators known as synchrotrons or synchro-cyclotrons are used, which can adjust the oscillator frequency to match the increasing velocity of particles as they spiral out. This adjustment allows for the acceleration of particles to speeds much closer to the speed of light.

Mindmap

Keywords

💡Cyclotron

A cyclotron is a type of particle accelerator that uses a combination of magnetic and electric fields to accelerate charged particles in a spiral path outwards towards a higher energy state. In the video, the cyclotron is the central theme, as it discusses how the device accelerates particles and the importance of the electric field flipping at the right moment to maintain acceleration.

💡Oscillating Electric Fields

Oscillating electric fields refer to electric fields that change direction periodically. In the context of the video, these fields are crucial for the acceleration of charged particles within a cyclotron, as they provide the force needed to speed up the particles each time they re-enter the field after being deflected by the magnetic field.

💡Magnetic Fields

Magnetic fields play a pivotal role in a cyclotron by influencing the trajectory of charged particles. As particles are accelerated by the electric field, the magnetic field causes them to turn and follow a spiral path, allowing them to re-enter the oscillating electric field and continue accelerating.

💡Charged Particle

A charged particle is any particle that carries an electric charge, such as protons or ions. In the video, the script discusses the acceleration of a proton, a type of charged particle, within the cyclotron, highlighting how its charge allows it to interact with the electric and magnetic fields.

💡Frequency

Frequency in the context of the video refers to how often the electric field in a cyclotron flips direction to maintain the acceleration of the charged particles. The script explores whether this frequency should be constant or changing and how it can be calculated to ensure the cyclotron operates effectively.

💡Spiral Motion

Spiral motion describes the path taken by charged particles as they are accelerated in a cyclotron. The script mentions this motion to illustrate the complexity of the particle's trajectory and to consider how the frequency of the electric field flipping should correspond to this motion.

💡Oscillator

An oscillator in the video refers to the system that controls the flipping of the electric field in the cyclotron. The script discusses the design considerations for this oscillator, including whether its frequency should remain constant or vary, and how to calculate the correct frequency for particle acceleration.

💡Time Period

The time period is the duration of one complete cycle of the oscillating electric field. The video script emphasizes that the time period of the oscillator should match the time it takes for a charged particle to complete one spiral in the cyclotron, which is a key factor in the successful operation of the device.

💡Relativity

Relativity, specifically Einstein's theory of relativity, is mentioned in the script to highlight a limitation of cyclotrons. As particles approach the speed of light, their mass increases, which affects the constant frequency of the oscillator. The script uses relativity to explain why cyclotrons cannot accelerate particles to speeds close to the speed of light.

💡Synchrotron

A synchrotron is a type of particle accelerator that overcomes the limitations of cyclotrons by adjusting the frequency of the oscillator as particles accelerate and their speed increases. The script briefly mentions synchrotrons as modern accelerators that can handle particles approaching the speed of light by adjusting the oscillator frequency.

Highlights

Cyclotrons use oscillating electric fields to accelerate charged particles while magnetic fields make them turn and re-enter the electric field for continuous acceleration.

The electric field in a cyclotron flips at the right moment to ensure particles keep accelerating in a spiral motion.

The frequency of the electric field flipping in a cyclotron is a critical engineering consideration for proper operation.

The time it takes for a particle to complete one spiral in a cyclotron is equal to the time for one oscillation of the electric field.

The time to complete a spiral remains constant despite increasing radius due to the proportional increase in speed.

The time for one full spiral is calculated as 2πm/qb, where m is mass, q is charge, and b is the magnetic field strength.

The cyclotron frequency is the reciprocal of the time taken to complete one spiral and is a constant value for the oscillator.

The oscillator frequency must remain constant for the cyclotron to work efficiently as particles spiral outwards.

Einstein's theory of relativity shows that mass increases with velocity, affecting the cyclotron's constant frequency assumption at high speeds.

At speeds much smaller than the speed of light, the increase in mass due to relativity is negligible, and the cyclotron operates as expected.

Modern accelerators, such as synchrotrons, adjust the oscillator frequency to accommodate particles approaching the speed of light.

Synchro cyclotrons are capable of adjusting the oscillator frequency to keep in sync with the spiraling protons.

The basic principles of physics allow for the derivation of cyclotron operation without memorizing specific equations.

Centrifugal force provided by the magnetic field is key to understanding the motion of particles in a cyclotron.

The limitations of cyclotrons are primarily due to relativistic effects at high velocities, necessitating advanced accelerator designs.

The cyclotron's spiral motion and frequency considerations are fundamental to understanding particle acceleration in magnetic fields.