Probabilistic view of linear regression
Summary
TLDRThis video script explores the probabilistic perspective of linear regression, treating it as an estimation problem. It explains how the labels are generated through a probabilistic model involving feature vectors, weights, and Gaussian noise. The script delves into the maximum likelihood approach to estimate the weights, leading to the same solution as linear regression with squared error. It emphasizes the equivalence between choosing a noise distribution and an error function, highlighting the importance of Gaussian noise in justifying the squared error commonly used in regression analysis.
Takeaways
- 📊 The script introduces a probabilistic perspective on linear regression, suggesting that labels are generated through a probabilistic model involving data points and noise.
- 🔍 It explains that in linear regression, we are not modeling the generation of features themselves but the probabilistic relationship between features and labels.
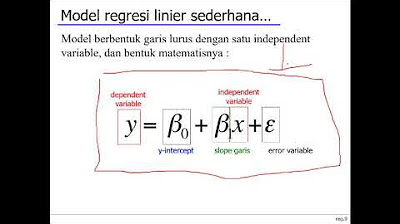
- 🎯 The model assumes that each label y_i is generated as w^T x_i + epsilon, where epsilon is noise, and w is an unknown fixed parameter vector.
- 📚 The noise epsilon is assumed to follow a Gaussian distribution with a mean of 0 and a known variance sigma^2.
- 🧩 The script connects the concept of maximum likelihood estimation to the problem of linear regression, highlighting that the maximum likelihood approach leads to the same solution as minimizing squared error.
- 📉 The likelihood function is constructed based on the assumption of independent and identically distributed (i.i.d.) data points, each following a Gaussian distribution influenced by the model's parameters.
- ✍️ The log-likelihood is used for simplification, turning the product of probabilities into a sum, which is easier to maximize.
- 🔧 By maximizing the log-likelihood, the script demonstrates that the solution for w is equivalent to the solution obtained from traditional linear regression with squared error loss.
- 📐 The conclusion emphasizes that the maximum likelihood estimator with 0 mean Gaussian noise is the same as the solution from linear regression with squared error, highlighting the importance of the noise assumption.
- 🔄 The script points out that the choice of error function in regression is implicitly tied to the assumed noise distribution, and different noise assumptions would lead to different loss functions.
- 🌐 Viewing linear regression from a probabilistic viewpoint allows for the application of statistical estimator theory to understand and analyze the properties of the estimator, such as hat{w}_{ML}.
- 💡 The script suggests that by adopting a probabilistic approach, we gain insights into the properties of the estimator and the connection between noise statistics and the choice of loss function in regression.
Q & A
What is the main focus of the script provided?
-The script focuses on explaining the probabilistic view of linear regression, where the relationship between features and labels is modeled probabilistically with the assumption of a Gaussian noise model.
What is the probabilistic model assumed for the labels in this context?
-The labels are assumed to be generated as the result of the dot product of the weight vector 'w' and the feature vector 'x', plus some Gaussian noise 'ε' with a mean of 0 and known variance σ².
Why is the probabilistic model not concerned with how the features themselves are generated?
-The model is only concerned with the relationship between features and labels, not the generation of the features themselves, as it is focused on estimating the unknown parameters 'w' that affect the labels.
What is the significance of the noise term 'ε' in the model?
-The noise term 'ε' represents the random error or deviation in the label 'y' from the true linear relationship 'w transpose x', and it is assumed to follow a Gaussian distribution with 0 mean and variance σ².
How does the assumption of Gaussian noise relate to the choice of squared error in linear regression?
-The assumption of Gaussian noise with 0 mean justifies the use of squared error as the loss function in linear regression, as it implies that the likelihood of observing a label 'y' given 'x' is maximized when the squared error is minimized.
What is the maximum likelihood approach used for in this script?
-The maximum likelihood approach is used to estimate the parameter 'w' by finding the value that maximizes the likelihood of observing the given dataset, under the assumption of the probabilistic model described.
What is the form of the likelihood function used in the script?
-The likelihood function is the product of the Gaussian probability densities for each data point, with each density having a mean of 'w transpose xi' and variance σ².
Why is the log likelihood used instead of the likelihood function itself?
-The log likelihood is used because it simplifies the optimization process by converting the product of likelihoods into a sum, which is easier to maximize.
What is the solution to the maximization of the log likelihood?
-The solution is to minimize the sum of squared differences between the predicted labels 'w transpose xi' and the actual labels 'yi', which is the same as the solution to the linear regression problem with squared error.
How does the script connect the choice of noise distribution to the loss function used in regression?
-The script explains that the choice of noise distribution (e.g., Gaussian) implicitly defines the loss function (e.g., squared error), and vice versa, because the loss function reflects the assumed statistical properties of the noise.
What additional insights does the probabilistic viewpoint provide beyond the traditional linear regression approach?
-The probabilistic viewpoint allows for the study of the properties of the estimator 'w hat ML', such as its statistical properties and robustness, which can lead to a deeper understanding of the regression problem.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
5.0 / 5 (0 votes)