IB Physics-Theme-A2- A student uses a load to pull a box up a ramp inclined
Summary
TLDRThis educational transcript discusses solving problems involving Newton's Laws of Motion, emphasizing the importance of free body diagrams and net force calculations. It covers a scenario where a student pulls a box up an inclined ramp with a load, detailing the steps to find tension in the string, the load's speed, angular speed of a pulley, and average frictional force. Two methods, Newton's Laws and conservation of energy, are used to solve each part, illustrating a comprehensive approach to physics problems.
Takeaways
- 📚 Always begin by drawing a free body diagram to visualize all forces acting on an object when solving Newton's Laws of Motion problems.
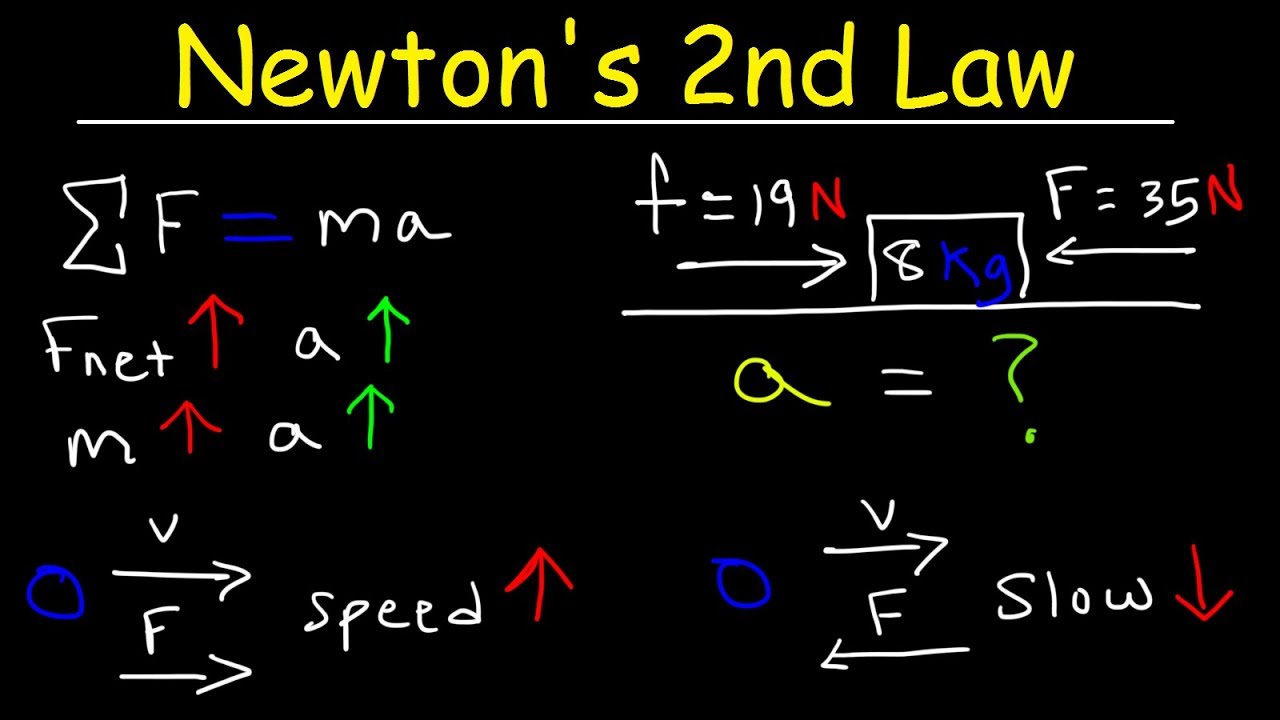
- 🧭 Determine the net force (F_net) by considering the direction of forces and acceleration, treating the direction of motion as positive.
- 🔢 Use the formula F_net = m * a to apply Newton's Second Law, where m is mass and a is acceleration.
- 💡 Newton's First Law states that if an object is at rest or moving at a constant speed, the net force acting on it is zero, resulting in no acceleration.
- 📉 When analyzing inclined surfaces, consider the components of weight acting parallel and perpendicular to the ramp, and the frictional force opposing motion.
- 🔄 Understand the difference between momentum (mass times velocity) of two objects with the same velocity but different masses and directions.
- 📌 Calculate tension in a string using Newton's Second Law, considering the forces acting on the heavier object and the acceleration.
- 🚀 To find the speed of an object, use either the SUVAT equations or the conservation of energy principle, depending on the situation.
- ⚙️ The angular speed (omega) can be found using the relationship between linear speed and radius, where omega = velocity / radius.
- 🛑 For an object coming to rest, use the SUVAT equation with a final velocity of zero to find the deceleration and then the average frictional force.
- 🔄 Conservation of energy can also be used to solve for frictional forces by equating initial kinetic energy to the work done against friction.
Q & A
What are the steps to follow when solving a problem related to Newton's Laws of Motion?
-The steps are: 1) Draw a free body diagram showing all forces acting on the object. 2) Determine the net force (total force), considering the direction of acceleration as positive. 3) Apply the formula F_net = m * a for Newton's second law, taking into account the direction of forces.
What is a free body diagram and why is it important in physics?
-A free body diagram is a graphical representation of all the forces acting on an object. It's important because it helps visualize and analyze the forces that influence the motion of an object, which is essential for applying Newton's laws correctly.
Why is the direction of acceleration considered positive when calculating the net force?
-The direction of acceleration is considered positive to simplify the calculation of net force. Forces that have the same direction as the acceleration are positive, and those opposite are negative, allowing for a straightforward summation of forces along the direction of motion.
What does Newton's first law state and when should it be applied?
-Newton's first law, also known as the law of inertia, states that an object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force. It is applied when the net force on an object is zero, resulting in no acceleration.
In the context of the inclined plane problem, what is the significance of the tension in the string?
-The tension in the string is significant because it is one of the forces acting on the load. It is calculated using Newton's second law to determine the acceleration of the load and is crucial for solving the dynamics of the system.
How is the momentum of the box and the load different in the inclined plane scenario?
-The momentum, which is mass times velocity, is different for the box and the load because they have different masses. Although they are attached to the same string and move with the same velocity, their masses result in different momenta and different directions of motion.
What is the formula used to calculate the tension in the string for the load in the inclined plane problem?
-The formula used is t = m(g - a), where m is the mass of the load, g is the acceleration due to gravity, and a is the vertical acceleration of the load.
How is the speed of the load determined when it hits the floor?
-The speed of the load can be determined using either the SUVAT equation v^2 = u^2 + 2as or the conservation of energy principle. Both methods consider the initial conditions, acceleration, and the vertical distance the load falls.
What is the relationship between linear speed and angular speed in the context of the poly?
-The relationship is given by v = ω * r, where v is the linear speed, ω is the angular speed, and r is the radius of the poly. This relationship is used to calculate the angular speed when the linear speed is known.
How can the average frictional force between the box and the ramp be determined?
-The average frictional force can be determined using Newton's second law by calculating the net force acting on the box as it comes to rest and then analyzing the forces to isolate the frictional force. Alternatively, conservation of energy can be used, considering the initial kinetic energy and the work done against friction.
Why does the student apply a constant force to the box after the box starts moving?
-A constant force is applied to overcome static friction, which is greater than the kinetic friction. Once the box is in motion, the static friction is replaced by kinetic friction, allowing the box to continue moving with the applied force.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen
5.0 / 5 (0 votes)