POLINÔMIOS - OPERAÇÕES COM POLINÔMIOS - Professora Angela Matemática
Summary
TLDRThis video teaches how to perform basic polynomial operations, including subtraction, multiplication, and division. The first example explains how to subtract polynomials, highlighting the distributive property and combining like terms. The second example covers multiplying polynomials, using the distributive property to multiply terms, and applying rules of exponents for the literal part of the terms. The third example focuses on dividing polynomials, illustrating both fraction and distributive methods. Throughout, the importance of combining like terms and applying mathematical rules correctly is emphasized, making this a practical tutorial for students learning polynomial operations.
Takeaways
- 😀 Subtraction of polynomials involves eliminating parentheses and combining like terms.
- 😀 To eliminate parentheses, copy each term exactly and distribute any multiplication outside parentheses using the distributive property.
- 😀 When multiplying a negative number with terms inside parentheses, the signs change according to the multiplication rules (e.g., minus times plus equals minus).
- 😀 Combining like terms is crucial when simplifying polynomials; this includes terms with the same variable and exponent.
- 😀 Degrees of polynomials are important when identifying like terms: terms must have the same base and exponent to be combined.
- 😀 In multiplication, when multiplying variables with the same base, add the exponents (e.g., a² × a² = a⁴).
- 😀 Division of polynomials can be approached by writing terms as fractions and simplifying each term individually.
- 😀 When dividing powers with the same base, subtract the exponents (e.g., x⁴ ÷ x² = x²).
- 😀 Division of polynomial terms can also be done using the distributive property, where each term is divided by the divisor.
- 😀 In polynomial division, cancel out terms that divide evenly and simplify the result step by step.
- 😀 Understanding sign rules in multiplication and division is critical for accurately simplifying polynomials, especially when negative terms are involved.
Q & A
What is the first step when subtracting polynomials?
-The first step is to eliminate the parentheses. For this, we copy each term inside the parentheses, keeping their signs, to simplify the expression.
How do we eliminate the parentheses in the subtraction of polynomials?
-To eliminate the parentheses, we simply copy the terms inside, taking care of the signs. If there is a negative sign outside the parentheses, we must apply the distributive property to change the signs accordingly.
What is the distributive property and how is it used in polynomial subtraction?
-The distributive property states that you multiply a number with each term inside the parentheses. In the case of subtraction, we apply this property by multiplying the negative number outside the parentheses with each term inside, changing their signs as needed.
Why do we not need to show the number 1 in front of terms like x or x² in polynomial operations?
-In polynomial operations, when no coefficient is shown, it implies that the coefficient is 1. For example, x is understood to be 1x, and the coefficient of x² is similarly 1.
What happens when we combine like terms in a polynomial?
-When combining like terms, we add or subtract the numerical coefficients while keeping the variable part (the literal part) the same. For example, -x³ and -3x³ combine to -4x³.
What are 'like terms' in polynomials?
-Like terms are terms that have the same variable(s) raised to the same power(s). For instance, x² and 3x² are like terms, but x² and x³ are not.
How do we handle multiplication with powers in polynomials?
-When multiplying powers with the same base, you keep the base and add the exponents. For example, a² × a² = a⁴.
What is the result of multiplying 3² by each term inside the parentheses (in the second example)?
-Multiplying 3² by each term inside the parentheses results in 3² × A² = A⁴, and 3² × 7ab = 21ab².
What is the rule for dividing powers with the same base in polynomials?
-When dividing powers with the same base, you subtract the exponents. For example, x⁴ ÷ x² = x².
How does the division of polynomials differ when using fractions versus distributive property?
-Using fractions, each term of the polynomial is divided individually by the denominator. With the distributive property, you apply the division to each term within the parentheses and simplify directly.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

JAGO EXCELL SEKEJAP RUMUS PENJUMLAHAN, PENGURANGAN, PEMBAGIAN, DAN PERKALIAN OTOMATIS

POLINÔMIOS #02 | ADIÇÃO E SUBTRAÇÃO COM POLINÔMIOS | \Prof. Gis/

Learn Fractions In 7 min ( Fast Review on How To Deal With Fractions)
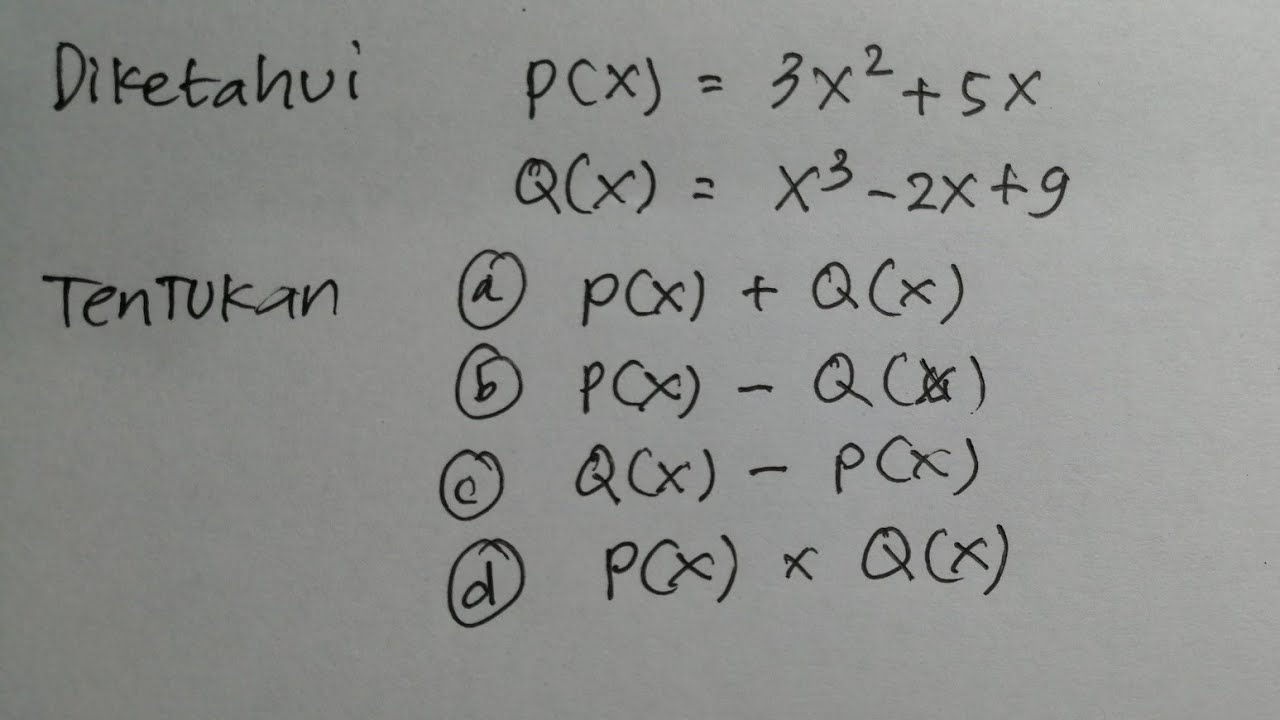
Penjumlahan, Pengurangan, dan Perkalian Suku Banyak Polinomial | Matematika SMA
Polynomials - Adding, Subtracting, Multiplying and Dividing Algebraic Expressions

CARA MUDAH PENJUMLAHAN PENGURANGAN PERKALIAN DAN PEMBAGIAN BENTUK AKAR
5.0 / 5 (0 votes)
