Diagramas de blocos e sua álgebra - parte 2

Summary

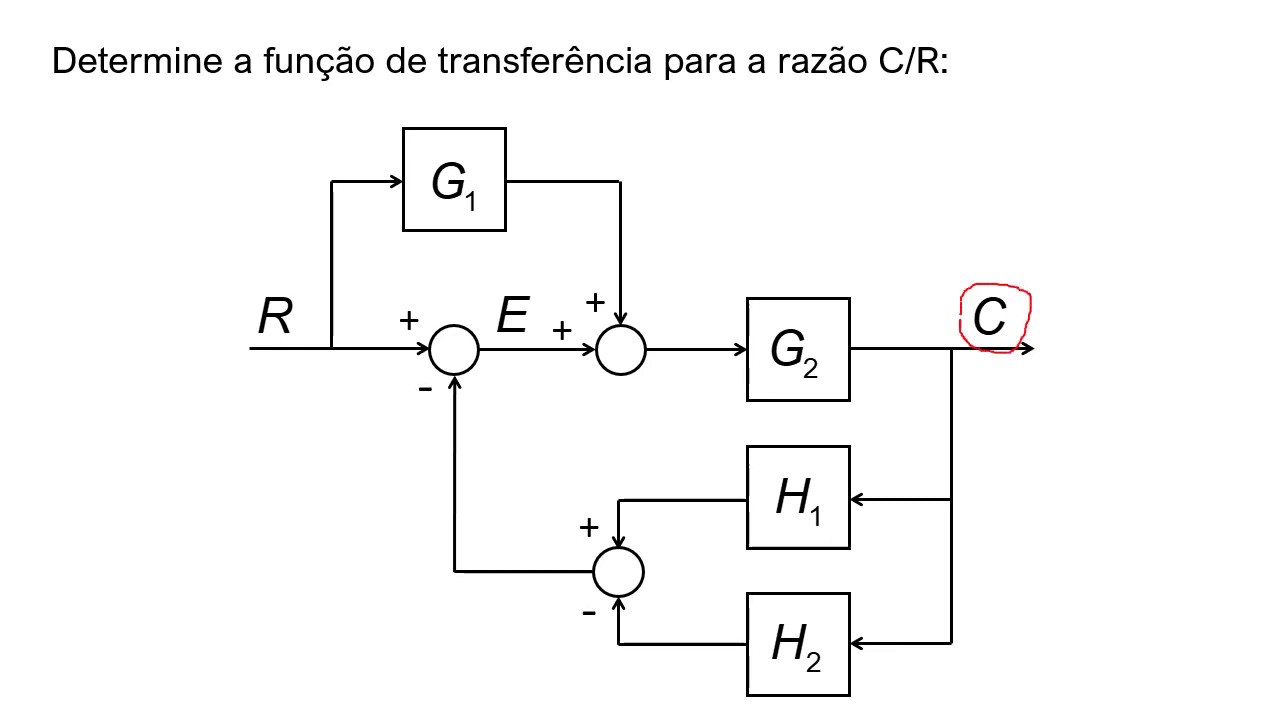
In this video, the speaker demonstrates how to apply block algebra techniques and mathematical operations to solve a control systems problem. The focus is on obtaining the transfer function of a system that relates the output variable to the set-point and feedback variables. By defining intermediate variables and using algebraic manipulations, the speaker simplifies the system’s equations, ultimately deriving a transfer function in terms of the variables of interest. The video is geared toward those familiar with control theory, offering a practical example to enhance understanding of block diagram analysis and problem-solving in this area.

Takeaways

• 😀 The script presents an example of applying block algebra techniques and mathematical operations to solve a control problem.
• 😀 The goal is to obtain the transfer function for a mesh that relates the variable 'y' with the variables 'y_sp' and 'y'.
• 😀 The mesh described is similar to a real-world control system, featuring components such as feedback sum points and process model operations.
• 😀 The video assumes viewers have already studied the theoretical aspects of block algebra before engaging with the content.
• 😀 The author emphasizes the importance of defining intermediate variables to simplify complex calculations and prevent errors.
• 😀 A key intermediate variable, 'a', is introduced to help organize the equations and reduce unnecessary complexity.
• 😀 The equations derived are used to express the variable 'y' in terms of the system's variables, including 'y_sp' and other components.
• 😀 The use of algebra is essential in simplifying and decoding the transfer function through a series of equation manipulations.
• 😀 The negative sign of intermediate variables is taken into account when manipulating equations to define new relationships.
• 😀 After algebraic simplification, the final expression for 'y' in terms of 'y_sp' is obtained, with all intermediate variables eliminated.
• 😀 The process illustrates how, by adhering to algebraic rules, complex control systems can be simplified and understood through block algebra.

Q & A

What is the main goal of the problem discussed in the video?

The main goal is to obtain the transfer function for the given mesh that relates the variable 'y' with the variables 'ysp' and others, focusing on applying block algebra techniques.

Why does the speaker define intermediate variables in the problem-solving process?

The speaker defines intermediate variables, like 'a', to simplify the problem, avoid excessive complexity, and make the algebraic manipulations more manageable.

What is the significance of using the intermediate variable 'a' in the script?

The intermediate variable 'a' helps organize the equations and keeps the calculation process lean, making it easier to solve without getting lost in too many variables.

How is the variable 'a' defined in the script?

'a' is defined as the difference between 'y' and 'ho-ho', which is written as a = y - ho-ho.

What is the function of the sum point involving 'a' and 'ysp' in the mesh?

The sum point involving 'a' and 'ysp' relates the error of the set-point and measurement. It receives a positive 'ysp' and a negative 'a', which helps define the system's behavior.

Why does the speaker focus on eliminating intermediate variables?

Eliminating intermediate variables simplifies the equations, ultimately leading to a transfer function that expresses 'y' in terms of 'ysp' and other relevant variables.

What algebraic manipulation does the speaker perform to simplify the equations?

The speaker applies algebraic manipulations such as isolating terms, moving them across the equation, and simplifying the expressions to highlight 'y' in terms of 'ysp' and other variables.

How does the speaker organize the terms to simplify the transfer function?

The speaker groups terms that involve 'y' on the left-hand side and factors involving 'ysp' and other variables on the right-hand side, followed by simplifying the equation by finding the least common multiple.

What does the speaker do to obtain the final simplified transfer function?

The speaker arranges the terms and factors them in a way that isolates 'y' in terms of 'ysp' and other variables, ultimately simplifying the transfer function.

What is the educational purpose of this video on block algebra?

The purpose is to teach viewers how to apply block algebra techniques to real-world control systems problems, helping them understand how to solve for transfer functions and manage complex algebraic equations.