Razones trigonométricas | Aplicación con dos triángulos | Ejemplo 2
Summary
TLDREn este video, se explica de manera clara y detallada cómo aplicar las razones trigonométricas para resolver ejercicios con triángulos rectángulos. El instructor aborda cómo identificar los triángulos adecuados para trabajar, cómo aplicar fórmulas como el seno y la tangente, y cómo usar los ángulos y lados conocidos para encontrar los valores desconocidos en un problema. A través de ejemplos prácticos y explicaciones paso a paso, se enseña cómo calcular los lados de los triángulos y se invita a los espectadores a practicar con ejercicios adicionales para reforzar los conceptos aprendidos.
Takeaways
- 😀 Es importante recordar que estamos trabajando con triángulos rectángulos, donde solo se usan los ángulos y los lados para encontrar los valores desconocidos.
- 😀 La función trigonométrica utilizada para encontrar el lado opuesto a un ángulo es el seno (sine).
- 😀 El valor del seno de un ángulo es igual al cateto opuesto dividido entre la hipotenusa.
- 😀 Para resolver el problema, primero se identifican los datos conocidos, como el ángulo y la hipotenusa.
- 😀 El primer paso en los ejercicios fue calcular el cateto opuesto en el triángulo grande utilizando la fórmula del seno.
- 😀 Luego de encontrar el cateto opuesto, ese valor se utiliza en el segundo triángulo, que comparte ese cateto como lado común.
- 😀 En el triángulo pequeño, se utiliza la tangente para encontrar el valor desconocido, el cateto adyacente.
- 😀 La tangente de un ángulo es igual al cateto opuesto dividido entre el cateto adyacente.
- 😀 Es importante verificar que las calculadoras estén en modo grados al realizar cálculos trigonométricos.
- 😀 El proceso implica primero resolver el triángulo grande y luego transferir la información obtenida a los otros triángulos para continuar con los cálculos.
Q & A
¿Qué tipo de triángulos se utilizan en el ejercicio explicado en el video?
-En el ejercicio se utilizan dos triángulos rectángulos: uno grande y otro pequeño. El triángulo a la izquierda no es un triángulo rectángulo y no se usa para resolver el ejercicio.
¿Cómo se identifican los triángulos que se deben utilizar?
-Los triángulos que se deben utilizar son aquellos que tienen un ángulo recto. En este caso, se usan el triángulo grande y el pequeño, ambos rectángulos, mientras que el triángulo a la izquierda no se usa.
¿Qué información se conoce sobre el triángulo grande?
-En el triángulo grande, se conoce el ángulo de 32 grados, el ángulo recto, y la hipotenusa que mide 15 metros.
¿Qué fórmula trigonométrica se utiliza para encontrar el valor de la pierna opuesta en el triángulo grande?
-Se utiliza la fórmula del seno, ya que conocemos el ángulo de 32 grados y la hipotenusa. La fórmula es: seno de 32 grados = pierna opuesta / 15 metros.
¿Qué resultado se obtiene al aplicar la fórmula del seno en el triángulo grande?
-Al aplicar la fórmula del seno, se obtiene que la pierna opuesta mide 7.94 metros.
¿Cómo se determina el valor de 'x' en el triángulo pequeño?
-En el triángulo pequeño, se usa la tangente, ya que conocemos la pierna opuesta (7.94 metros) y el ángulo de 63 grados, y queremos encontrar la pierna adyacente, que es 'x'.
¿Qué fórmula trigonométrica se utiliza para resolver el triángulo pequeño?
-Se utiliza la fórmula de la tangente: tangente de 63 grados = pierna opuesta / pierna adyacente (x).
¿Cuál es el resultado al resolver la ecuación para 'x' en el triángulo pequeño?
-Al resolver la ecuación, se obtiene que 'x' es igual a 4.04 metros.
¿Cómo se resuelve el ejercicio adicional propuesto al final del video?
-Para resolver el ejercicio adicional, primero se encuentra el lado común a ambos triángulos, luego se utiliza el seno para calcular el valor de la pierna opuesta y la tangente para encontrar 'x' en el segundo triángulo.
¿Qué se debe hacer si no recuerdas las fórmulas trigonométricas durante el ejercicio?
-Si no recuerdas las fórmulas trigonométricas, el video las explica detalladamente, y puedes consultarlas en los videos anteriores del curso para reforzar los conceptos.
Outlines

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenMindmap

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenKeywords

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenHighlights

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenTranscripts

Dieser Bereich ist nur für Premium-Benutzer verfügbar. Bitte führen Sie ein Upgrade durch, um auf diesen Abschnitt zuzugreifen.
Upgrade durchführenWeitere ähnliche Videos ansehen

Razones Trigonométricas
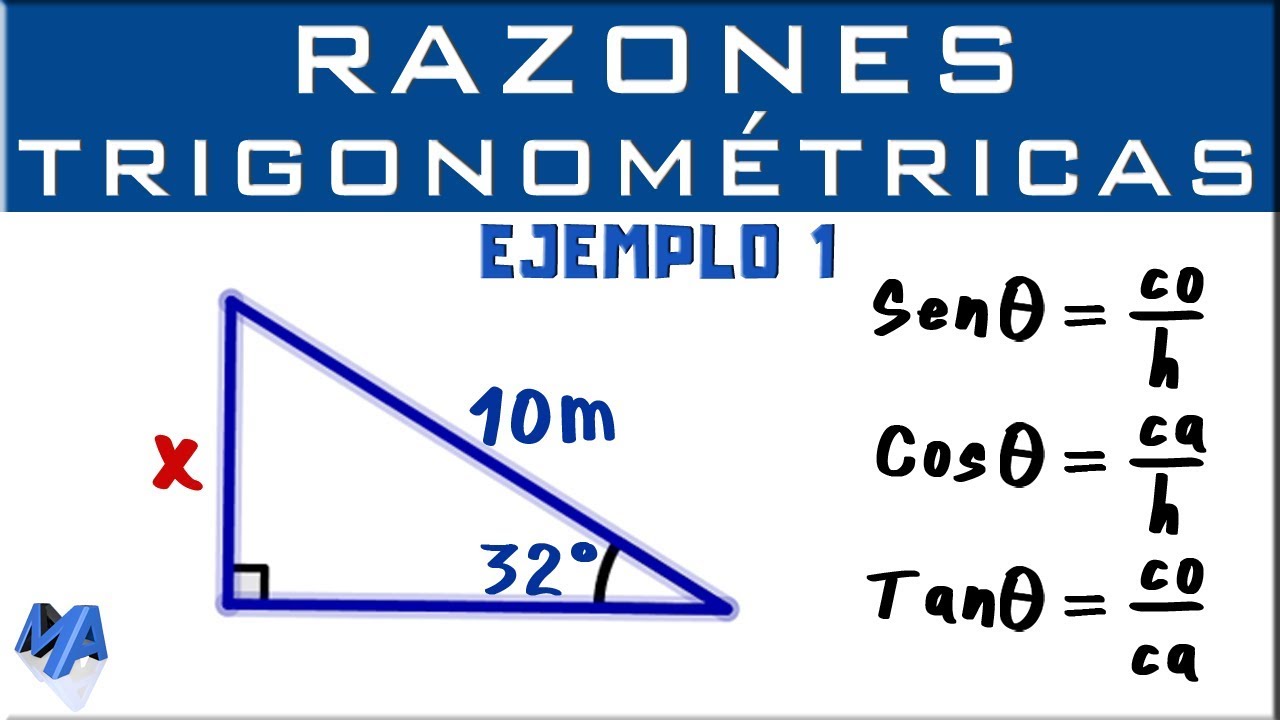
Razones Trigonométricas | Hallar un lado | Ejemplo 1

Círculo trigonométrico (PRIMERA PARTE)

Signos de las Razones Trigonométricas (NIVEL 2)

Usar relaciones en triángulos rectángulos para aproximar la medida de un ángulo

Matemática 1 TRIGONOMETRÍA 2da parte funciones trigonométricas en triángulos cualquiera
5.0 / 5 (0 votes)
