(Audio corrected) 9. Vorticity 1 of 2

Summary

This video explores the concept of vorticity in fluid dynamics, demonstrating its importance in understanding fluid flows. The script discusses how vorticity is defined, the role of vortex lines and angular velocity, and the use of a vorticity meter to measure it in various fluid scenarios. It explains how vorticity relates to boundary layers, circulation, and the dynamics of fluid motion, including the impact of forces like viscosity and body forces. The video also touches on the role of Coriolis forces in large-scale systems like the Earth's atmosphere and oceans, showcasing the principles with experimental examples.

Takeaways

• 😀 Vorticity measures the angular momentum of a small fluid particle around its center of mass, indicating rotational motion in a fluid.
• 😀 The angular velocity of a solidified fluid particle at the moment of freezing is half the vorticity of the fluid before freezing.
• 😀 Vorticity is defined as the curl of the velocity vector in a fluid, and vortex lines represent the local axis of spin for each fluid particle.
• 😀 A rigid body has uniform vorticity, meaning its vorticity is the same at every point and equals twice the angular velocity.
• 😀 The vorticity meter detects the average angular velocity of two mutually perpendicular fluid lines, indicating vorticity in the water.
• 😀 In boundary layers, even if flow is straight, the fluid may rotate near walls due to varying velocity distributions, signifying vorticity.
• 😀 Vorticity may be zero in some curved flows, as seen in the spiral vortex tank where no rotation occurs, even though the flow is curved.
• 😀 Kelvin and Helmholtz’s dynamical theorems describe how forces acting on fluid particles affect their vorticity over time.
• 😀 Coase's theorem connects vorticity with stagnation pressure gradients in steady, incompressible, non-viscous fluid flows.
• 😀 Circulation, defined as the line integral of velocity around a closed curve, relates directly to the vorticity passing through the area bounded by the curve.
• 😀 Viscous forces can change the circulation and vorticity of a fluid, gradually transforming the motion into solid body rotation in some cases, as seen in a tank of water.

Q & A

What is vorticity, and how is it defined in fluid dynamics?

Vorticity is a measure of the moment of momentum of a small spherical fluid particle about its own center of mass. It is defined as the curl of the velocity vector in fluid dynamics, and each fluid particle has a certain vector vorticity.

What is the role of vorticity in understanding fluid flows?

Vorticity helps to understand the rotation and motion of fluid particles, as well as how forces affect the movement of fluids. It provides insight into the dynamics of flow, such as how fluid rotates or behaves under various forces.

How does the vorticity meter work in fluid dynamics experiments?

The vorticity meter consists of two veins immersed in fluid, which rotate at angular velocities based on the vorticity of the fluid. The float's rotation rate is a measure of the average angular velocity of the fluid, indicating the vorticity in that region.

How does vorticity behave in a rigid body rotation?

In a rigid body rotation, every point in the fluid has the same angular velocity. The vorticity in such a system is constant and is exactly twice the angular velocity of the body.

What is the difference between rotation and vorticity in fluid dynamics?

Rotation refers to the actual turning of fluid particles, while vorticity is a mathematical description of the rotational motion of the fluid, specifically the curl of the velocity vector. A flow may have vorticity without visible rotation, especially in straight flows or boundary layers.

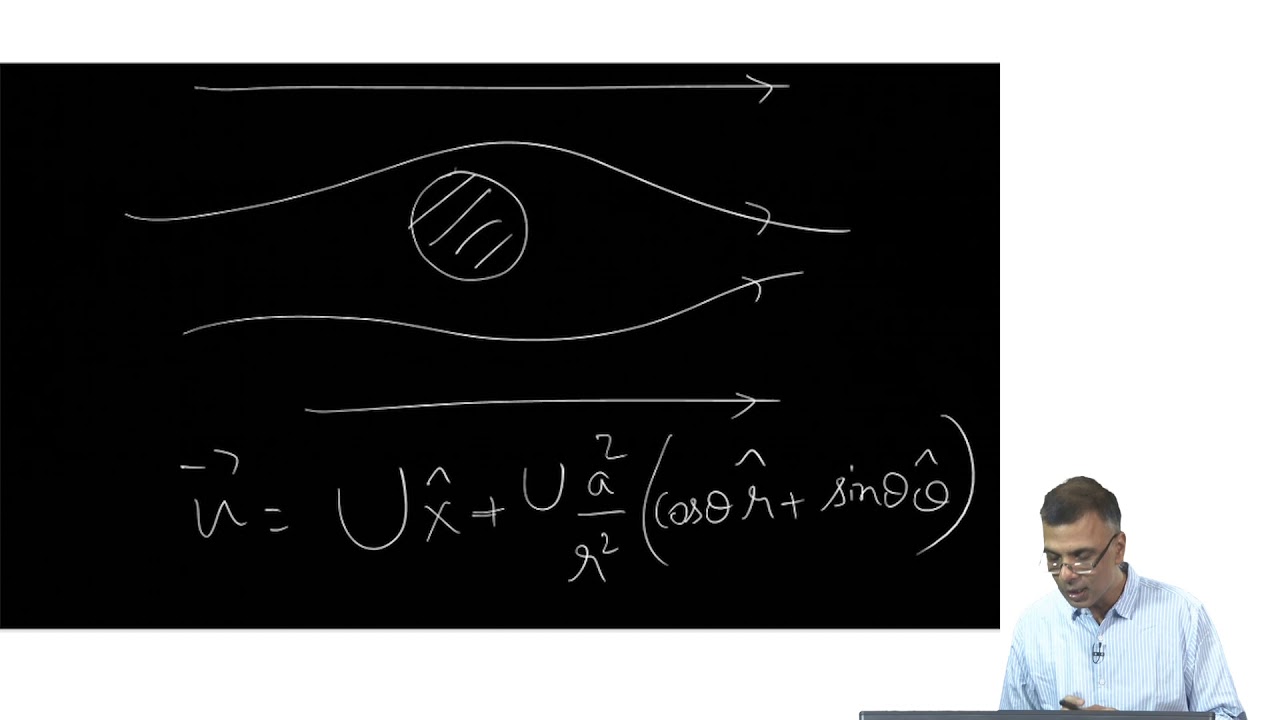
Can vorticity exist in a curved flow, and how is it measured?

Yes, vorticity can exist in curved flows, such as spiral vortex flows. Even though the flow may be curved, the vorticity meter may not rotate if the total vorticity is zero, as in certain symmetrical vortex systems.

What is Cauchy’s theorem and how does it relate to vorticity?

Cauchy’s theorem is a form of the dynamical equations of motion that states that if the flow is steady, incompressible, and free of viscous forces, the vector product of the velocity vector and the vorticity vector is equal to the gradient of the stagnation pressure divided by the density.

How does the concept of circulation relate to vorticity?

Circulation is defined as the line integral of the velocity around a closed curve. According to the circulation theorem, the circulation around a curve is equal to the flux of the vorticity passing through the area enclosed by the curve. If the circulation is zero, the fluid is free of vorticity.

What is the significance of the vortex core in a fluid flow?

The vortex core is a concentrated region of vorticity within a flow, where the vorticity is very large. The surrounding fluid may be free of vorticity. This concentration of vorticity is important in understanding the behavior of fluid flows and can be modeled as a concentrated vortex.

How do body forces like gravity and the Coriolis effect influence vorticity?

Body forces such as gravity are irrotational and do not change vorticity directly. However, rotational body forces like the Coriolis effect in a rotating reference frame can change the circulation and vorticity in the fluid, influencing flow dynamics, such as in atmospheric or oceanic systems.